Gráficas circulares e histogramas
Gráficas circulares e histogramas
Aprendizaje esperado: compara la tendencia central (media, mediana y moda) y la dispersión (rango y desviación media) de dos conjuntos de datos.
Énfasis: dar sentido y significado a las gráficas circulares e histogramas.
¿Qué vamos a aprender?
Ten a la mano tu cuaderno, lápiz y goma.
¿Qué hacemos?
¿Te acuerdas cuantos compañeros tienes en tu grupo?
Por ejemplo, en un grupo, específicamente 3°D, hay 40 estudiantes en total y son 14 alumnas y 26 alumnos.

Las edades de los alumnos varían entre 13 y 15 años.
Es posible usar una tabla de frecuencias para ordenarlas. Los datos se agrupan en dos intervalos, los que tienen 13 y 14 años y los que tienen 15 y 16 años.
Una vez ordenados, se representan mediante un histograma.
Para construir un histograma con los datos anteriores, observa el siguiente video del inicio a 01:26 y anota en tu cuaderno las características para construir uno.
- Histograma
https://youtu.be/o9D5fAQ07R8
Con las características mencionadas en el video, con los datos del grupo tercero “D”, en cuanto a sus edades, se ordenan en una tabla de frecuencia luego se representan con un histograma de la siguiente forma.
Ordenados los datos de mayor a menor se agrupan en dos clases, 13 y 14 años, y, 15 y 16 años.
Con los datos ordenados se llena la tabla de frecuencias.
En la tabla de frecuencia se anota que hay 22 alumnos con 13 y 14 años y, 18 alumnos con 15 y 16 años.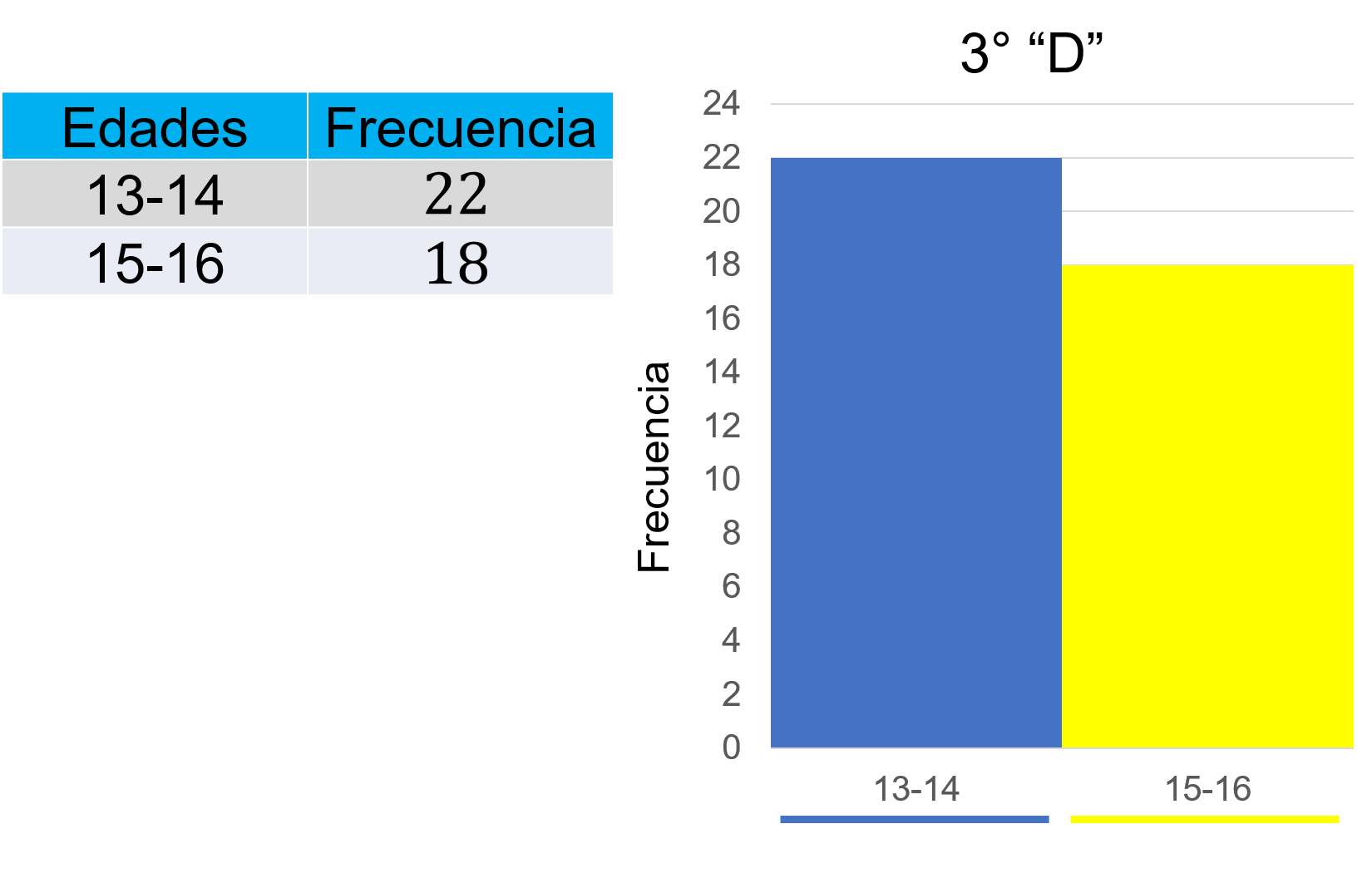
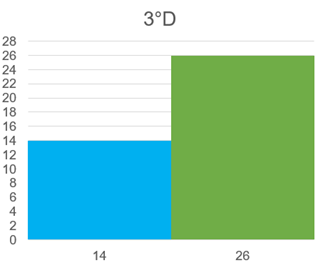
Con estos datos el eje horizontal se anotan los intervalos 13-14 y 15-16, en el eje vertical la frecuencia 22 y 18 respectivamente.
Para realizar el histograma del número de alumnas y alumnos del grupo tercero “D” en la tabla de frecuencias es de la siguiente forma.
En la tabla la frecuencia de las alumnas es de 14 y de alumnos 26.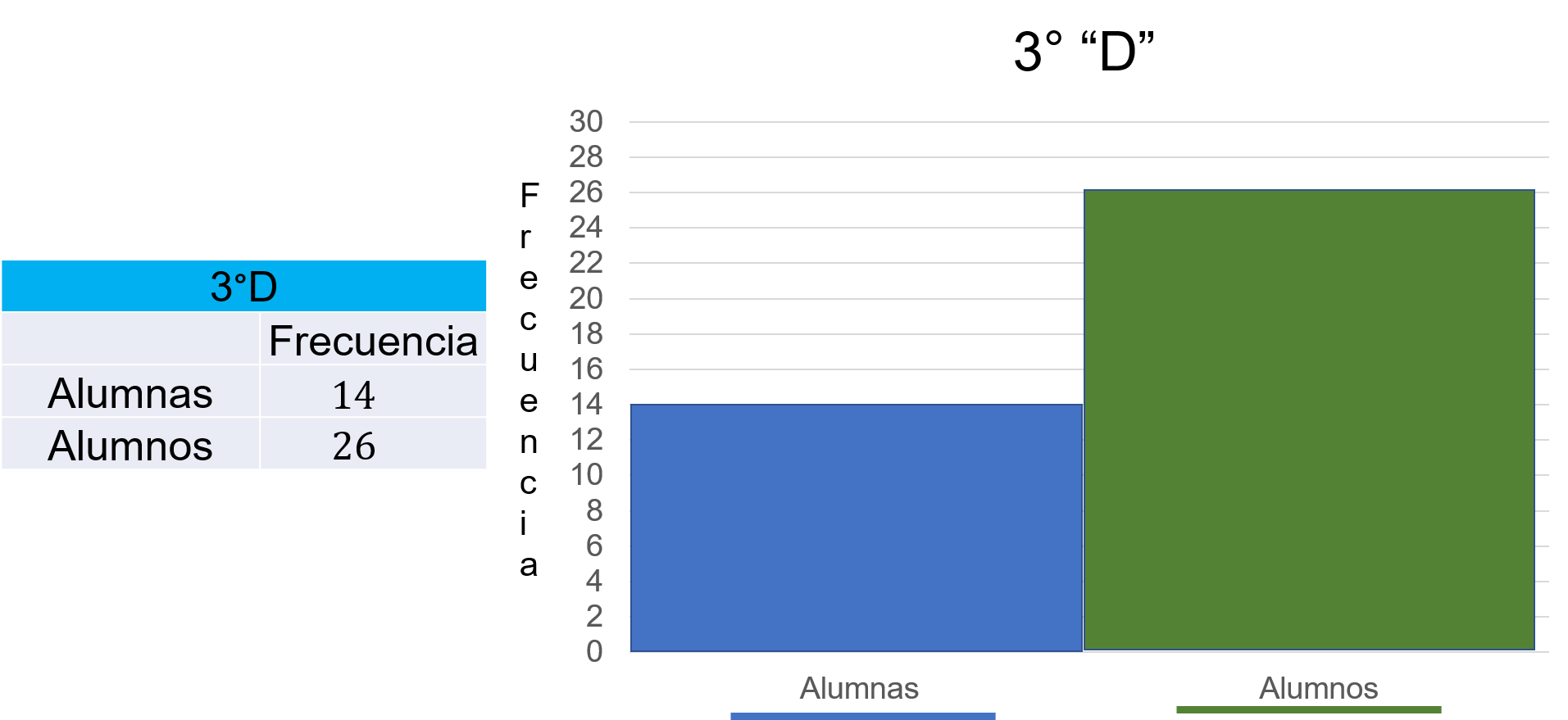
En el eje horizontal se representan dos categorías o clases, una es la de alumnas y la otra la de alumnos, así en el eje vertical indica la frecuencia de los datos para cada una de ellas.
La información del histograma de las edades del grupo muestra que hay más alumnos de 13 y 14 años en comparación con los quienes tienen 15 y 16 años.
En el histograma de alumnas y alumnos se denota una diferencia muy marcada entre ellos y, por con siguiente hay más alumnos en el grupo tercero “D”.
Esta es una forma de representar los datos sobre el grupo tercero “D”.
Estas gráficas permiten representar datos de variables cualitativas y cuantitativas, como es en este caso.
Existe otra forma de representar las cantidades y es mediante una gráfica circular. Observa cómo construir una que represente los datos de los alumnos de este grupo. Observa el siguiente video del minuto 01:35 a 04:10. - Elementos de una gráfica circular
En el video, observaste que la gráfica circular se utiliza para representar el porcentaje o proporción correspondiente a cada categoría de un conjunto de datos, esto a través de sectores.
Con los datos del grupo tercero “D”, calcula el porcentaje que representan las edades y el número de alumnas y alumnos en el grupo.
Para ello se utiliza una tabla como la siguiente.
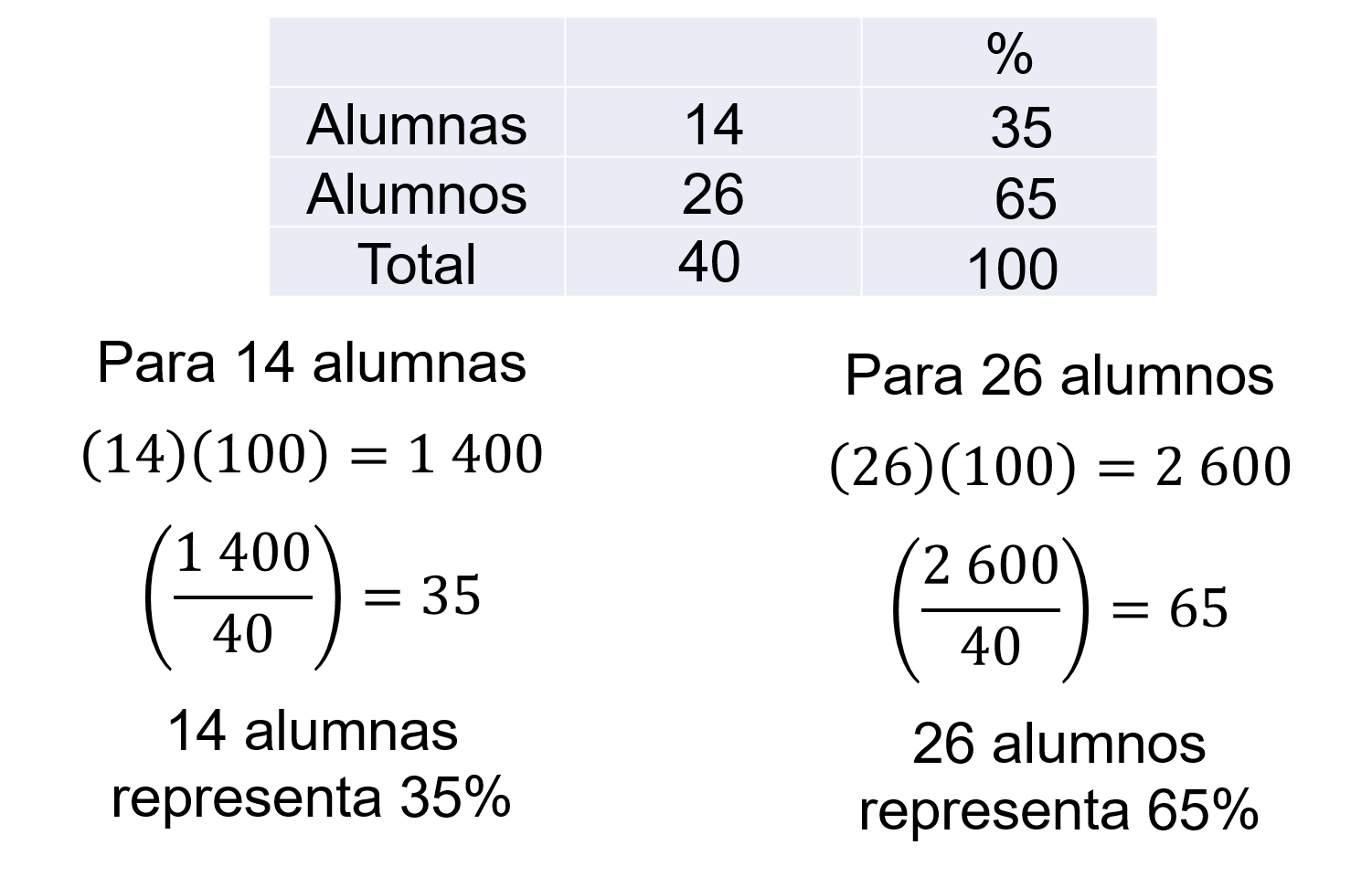
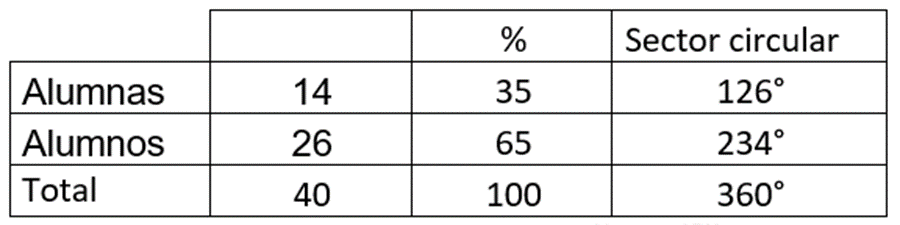
Para calcular el porcentaje de las 14 alumnas, se toma en cuenta el total de estudiantes, es decir, 40. Esta cantidad representa el 100 por ciento de alumnos del grupo.
Por tanto, se multiplica 14 por 100, se obtiene 1400, se divide entre 40, el resultado es 35. Así, 14 alumnas representan el 35 por ciento del grupo.
Para calcular el porcentaje de los 26 alumnos, se multiplica 26 por 100, se obtiene 2600, al dividirlo entre 40 el resultado es 65. 26 alumnos son el 65 por ciento del grupo.
Ya se tienen los porcentajes de cada categoría, pero ¿cómo se calcula el tamaño de cada sector para la gráfica circular?
La unidad de medida de un sector circular son los grados.
Un círculo comprende 360° y con un transportador es posible medir sectores de diversos tamaños.
La proporción que representa cada categoría respecto al total debe de guardar la misma proporción cada sector circular correspondiente respecto al círculo completo.
Es decir, al total de datos le corresponde el área que abarcan los 360 grados.
El ángulo que corresponde a cada categoría debe de cumplir con la siguiente proporción.
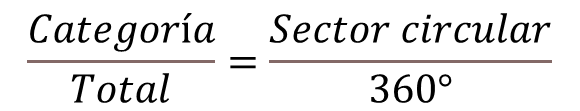
Por tanto, el ángulo para cada categoría es dado por:
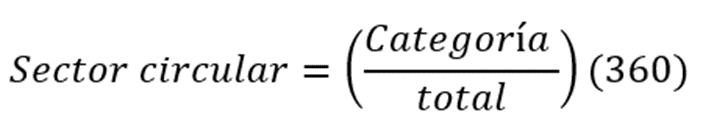
Con esta expresión calcula los sectores para los datos del grupo tercero “D”.
Al sustituir los valores en la expresión sector circular es igual a categoría entre el total, todo por 360 grados, se tiene:
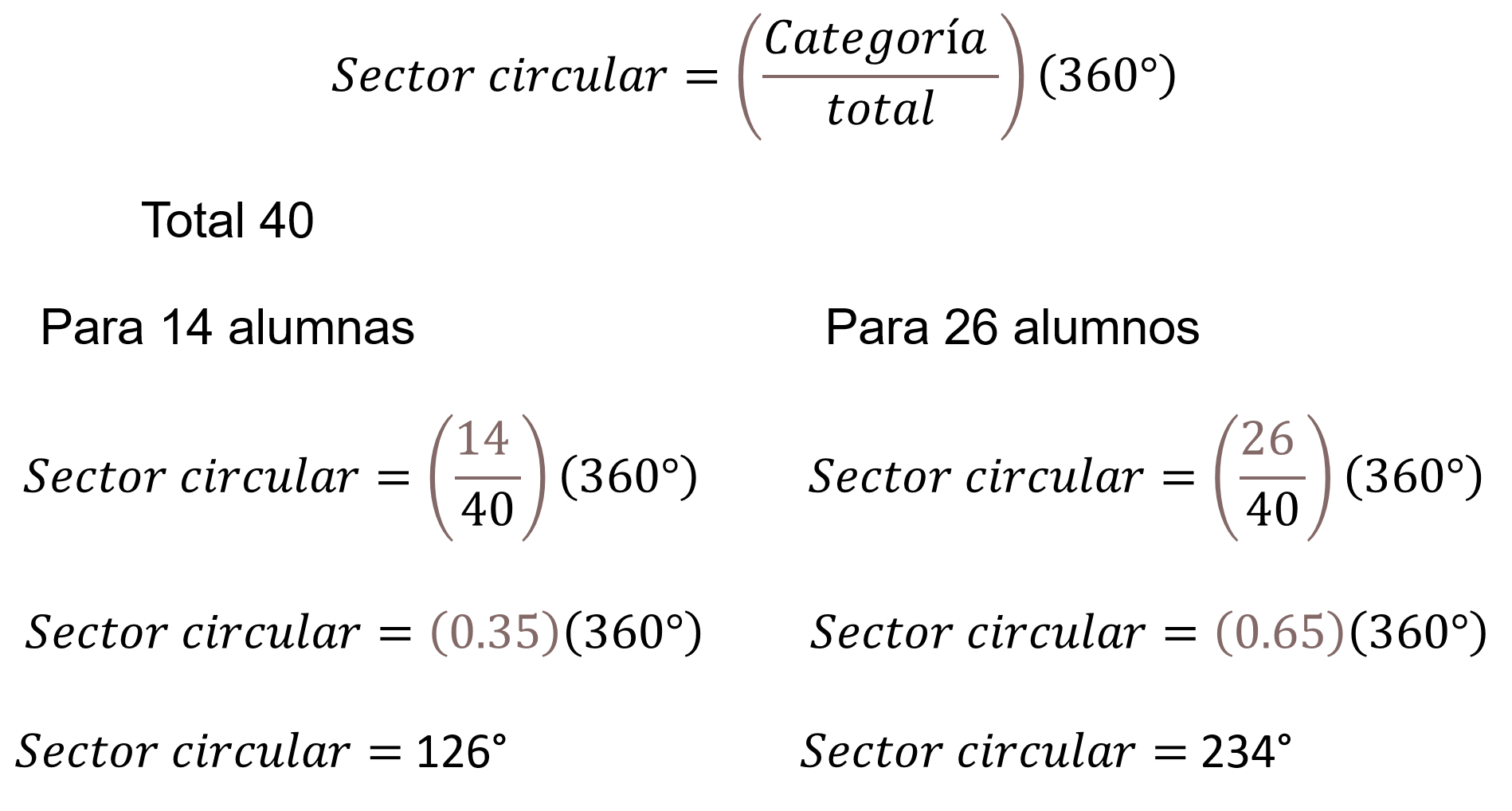
La categoría de alumnas su valor es 14.
El total es igual a 40.
El sector circular es igual a 14 por 40, por 360.
Al realizar las operaciones, es igual a 0.35 por 360, por lo tanto, el sector circular debe de medir 126 grados.
Para la categoría de 26 alumnos, el sector circular es igual a 26 entre 40, por 360, igual a 0.65 por 360, así el sector circular debe de medir 234 grados.
Los resultados obtenidos 126 grados y 234 grados, éstos representan la abertura del sector circular para cada categoría dentro de la gráfica.
Para realizar la gráfica circular, se traza una circunferencia de 10 cm de diámetro con el compás y con un transportador se marcan los ángulos obtenidos (126 y 234 grados), y para diferenciarlos, se sugiere utilizar un color distinto para cada uno.
Después de trazar la circunferencia, se coloca el transportador sobre la misma tomando como referencia el centro de la circunferencia, se mide y se traza un ángulo de 126 grados, posteriormente se colorea.
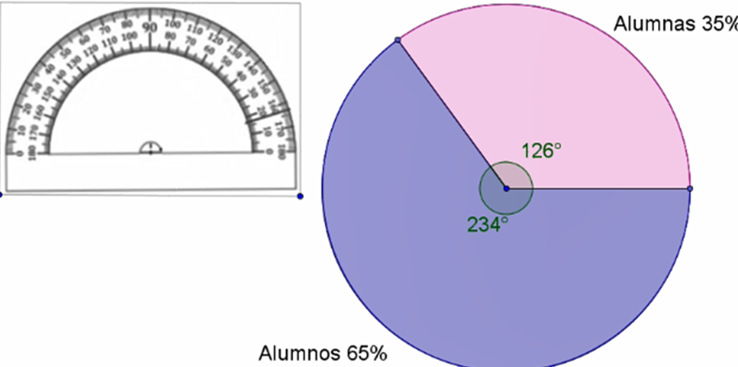
Como sólo son dos ángulos, el segundo automáticamente se traza pues si a 360 grados se le restan 126 grados, el resultado es 234 grados, se utiliza un color diferente para indicarlo.
Así quedan marcados los dos sectores de la gráfica, para terminar, se identifican al escribir el porcentaje correspondiente a la categoría que representa cada uno.
Los datos sobre el grupo tercero “D” son cuantitativos.
Con ellos se construyó un histograma.
Se trazó una gráfica circular utilizando los porcentajes correspondientes a cada dato o categoría del grupo.
En las dos gráficas se aprecian las diferencias entre los datos empleados.
Como es el caso del número de alumnas y alumnos del grupo.
Con base en ellas, si no se conocieran los datos específicos y sólo se tuviera la gráfica, al leerlas, en el caso del histograma sólo es posible decir el número de alumnas y alumnos del grupo tercero “D”.
Y en el caso de la gráfica circular es posible decir que, en el grupo tercero “D”, el 65% de los alumnos representa a los 26 alumnos varones en comparación con las alumnas, quienes representan el 35% del grupo.
Realiza la gráfica circular de las edades, calcula los porcentajes y apóyate en la tabla de frecuencia.
Para calcular el porcentaje de 22 alumnos de edades entre 13-14 años, se toma en cuenta el total de estudiantes 40.
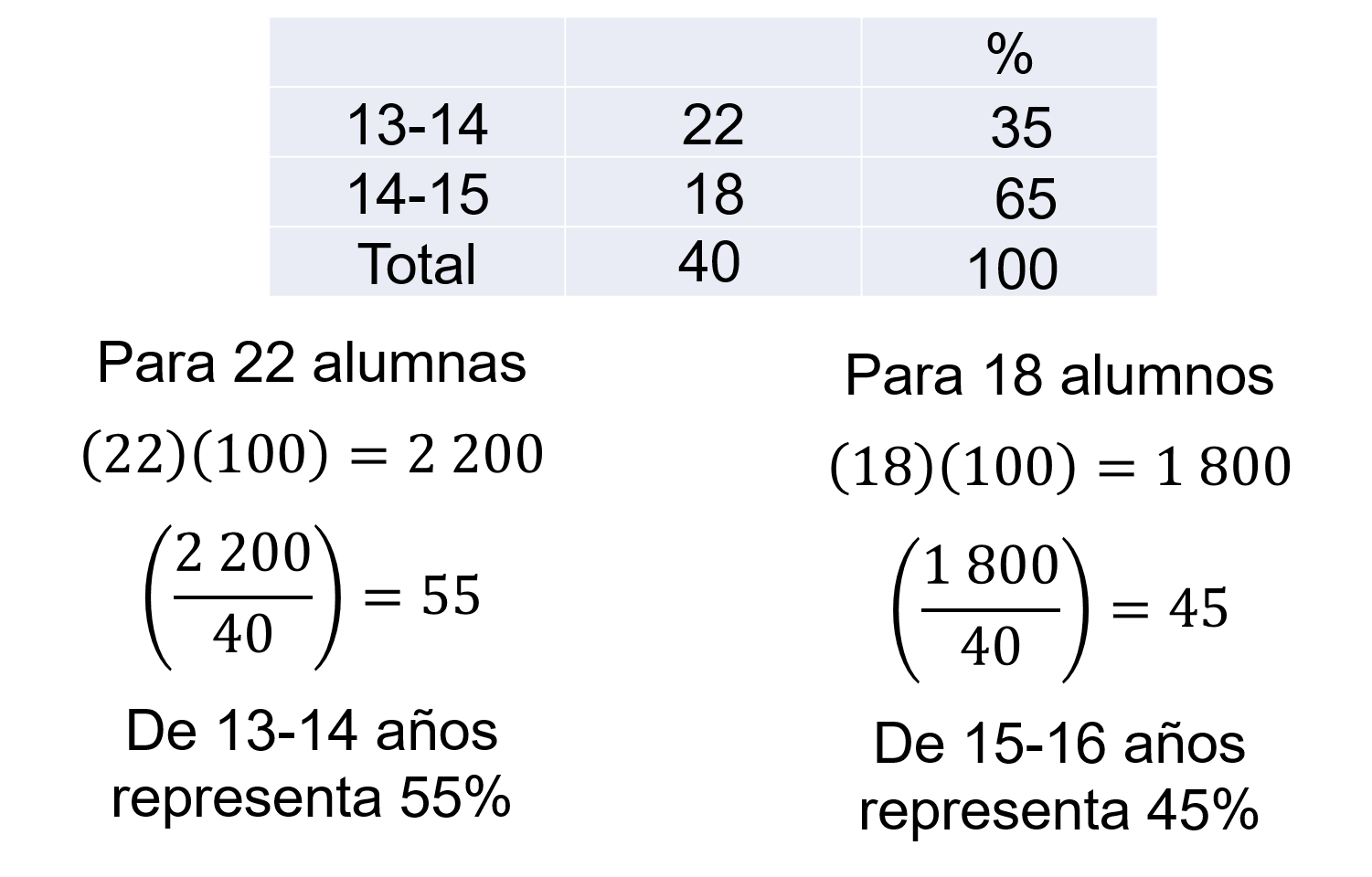
Esta cantidad representa el 100 por ciento de alumnos del grupo.
Por tanto, se multiplica 22 por 100, se obtiene 2200, se divide entre 40, el resultado es 55 por ciento.
Para calcular el porcentaje de 18 alumnos de edades entre 15-16 años se multiplica 18 por 100, se obtiene 1800, entre 40, el resultado es 45 por ciento.
Para calcular el sector circular de 22 alumnas es igual a 22 entre 40, igual a 0.55, multiplicado por 360, el ángulo es de 198°.
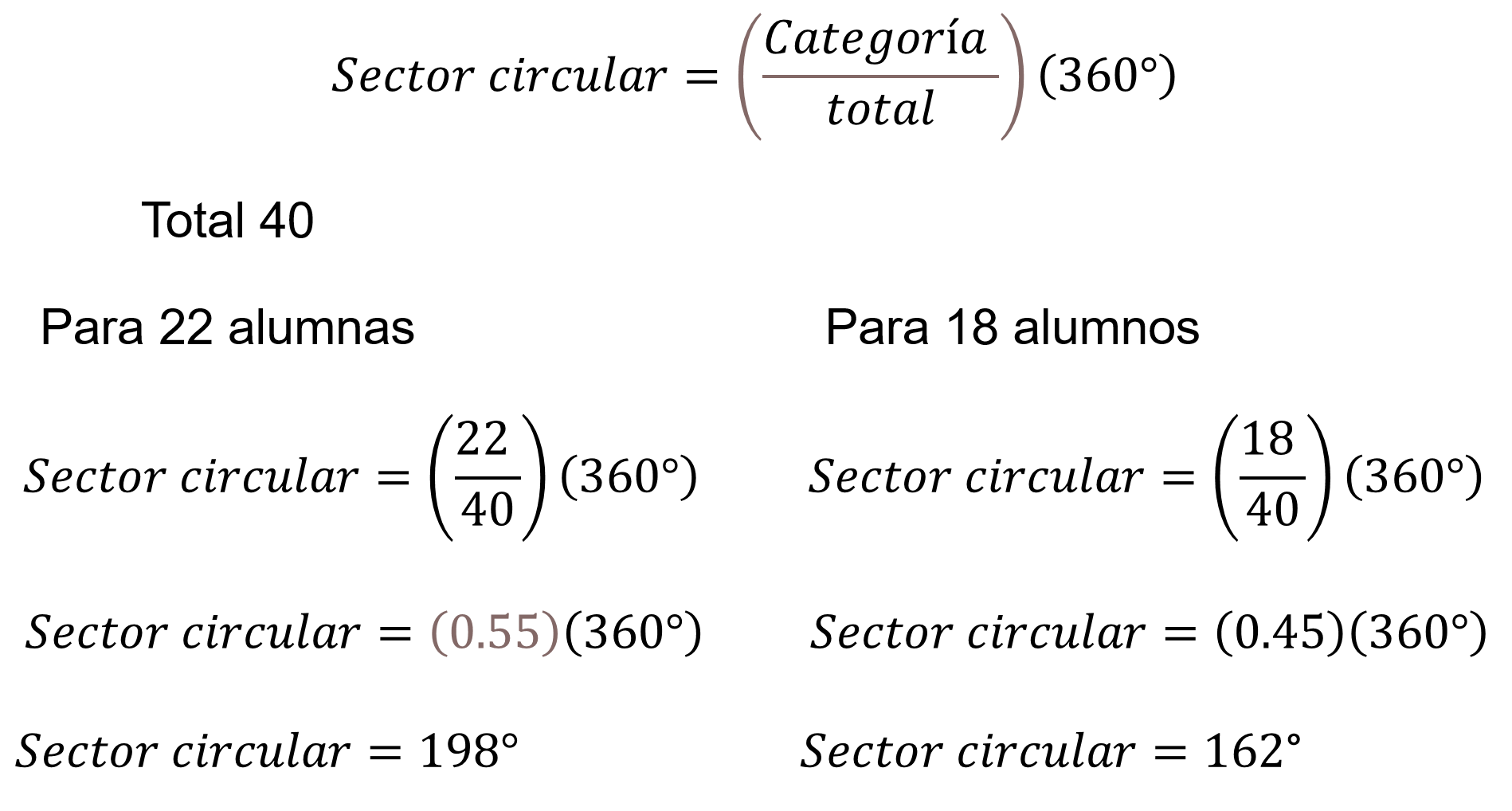
Para la categoría de 18 alumnos, el sector circular es igual a 18 entre 40, el cociente es 0.45 que, multiplicado por 360, da 162 grados.
Al trazar la gráfica circular, para 18 alumnos, se traza un ángulo de 162 grados el cual representa el 35 por ciento.
Para 22 alumnos, el ángulo que corresponde a es de 192 grados.
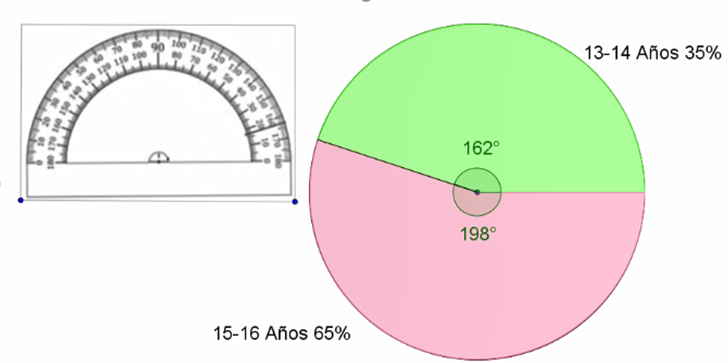
Como se puede observar en la gráfica circular y en el histograma, hay más alumnos con edades de 13 y 14 años que representan el 55% del grupo.
Las gráficas son una herramienta visual para distinguir características de un conjunto de datos permiten tener un mejor panorama de lo que representa cada sector.
Pero antes de construir las gráficas, se deben de organizar los datos para facilitar la apreciación de la información contenida.
Analiza el siguiente ejemplo. Ayuda a Bernardo, él es entrenador de fútbol y tiene que tomar una decisión.
Bernardo es entrenador de fútbol y acaba de terminar una temporada.
Bernardo debe de elegir a uno de sus tres mejores jugadores con el fin de darle el premio de “mejor jugador de la temporada”.
Para tomar una decisión de quién se lo merece, concentró varios datos de cada uno de los jugadores.
Revisa los datos; analízalos para ayudar a Bernardo a tomar la decisión.
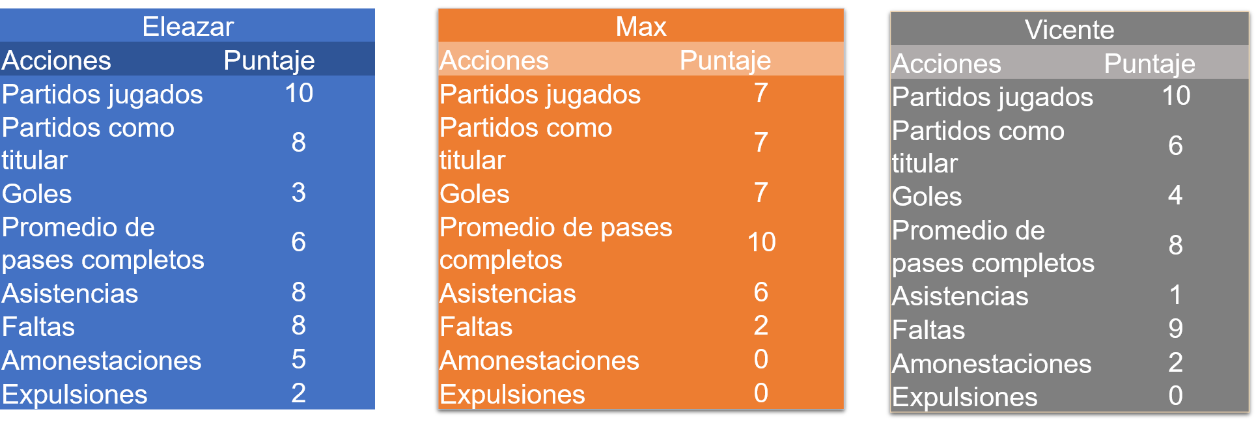
Dando un vistazo rápido a los datos de los tres jugadores, todos tienen muy distintas puntuaciones, en las diferentes acciones y es difícil decidir quién de ellos se merece el premio con estos datos.
Con los datos proporcionados por Bernardo no es posible aún tomar una decisión con facilidad.
Por ejemplo, Eleazar y Vicente han jugado diez partidos y Max sólo siete.
Pero Max anotó más goles en comparación a sus compañeros.
Además, Eleazar ha sido expulsado 2 veces y sus otros compañeros ninguna vez.
Formula cómo podrías ayudar a Bernardo a tomar una decisión a partir de los datos proporcionados.
Puedes representar los datos mediante un histograma y una gráfica circular.
Y con la información proporcionada por las gráficas, le ayudarás a Bernardo a tomar una decisión.
Para el histograma, las categorías son las acciones, y la frecuencia, son los puntajes de cada una de ellas.
A partir del análisis del histograma, se verá si es posible tomar la decisión a quién darle el premio.
Analiza el histograma, ¿es posible tomar la decisión?
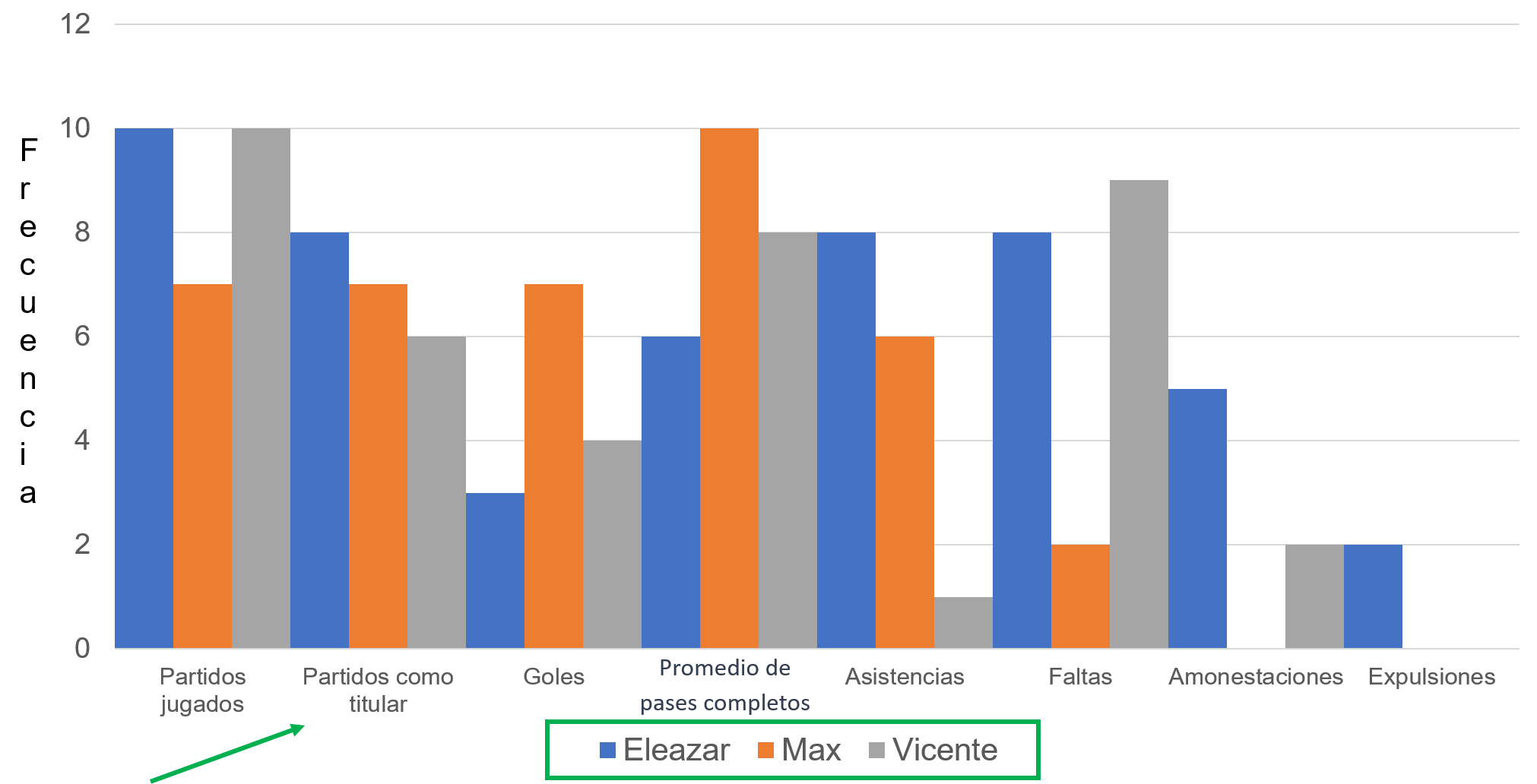
Observa que la información del histograma aun cuando están ordenados los datos a partir de las categorías con sus respectivas frecuencias, no está del todo claro.
El histograma permite tener una comparativa de cada jugador, pero aún no es suficiente para dar una opinión que ayude a tomar una decisión de quien se merece el premio.
Realiza una gráfica circular y observa si, con ella, es posible decidir a quién de los jugadores se le debe de dar el premio.
Pero antes, en la tabla agrupa las categorías en:
Acciones positivas. Partidos jugados, partidos como titular, goles, promedio de pases completos y asistencias.
Acciones negativas. Faltas, amonestaciones y expulsiones.
Observa si al estar agrupados en sólo dos categorías se tenga suficiente información del desempeño de los jugadores.
Al sumar el puntaje total de cada jugador, se obtuvo:
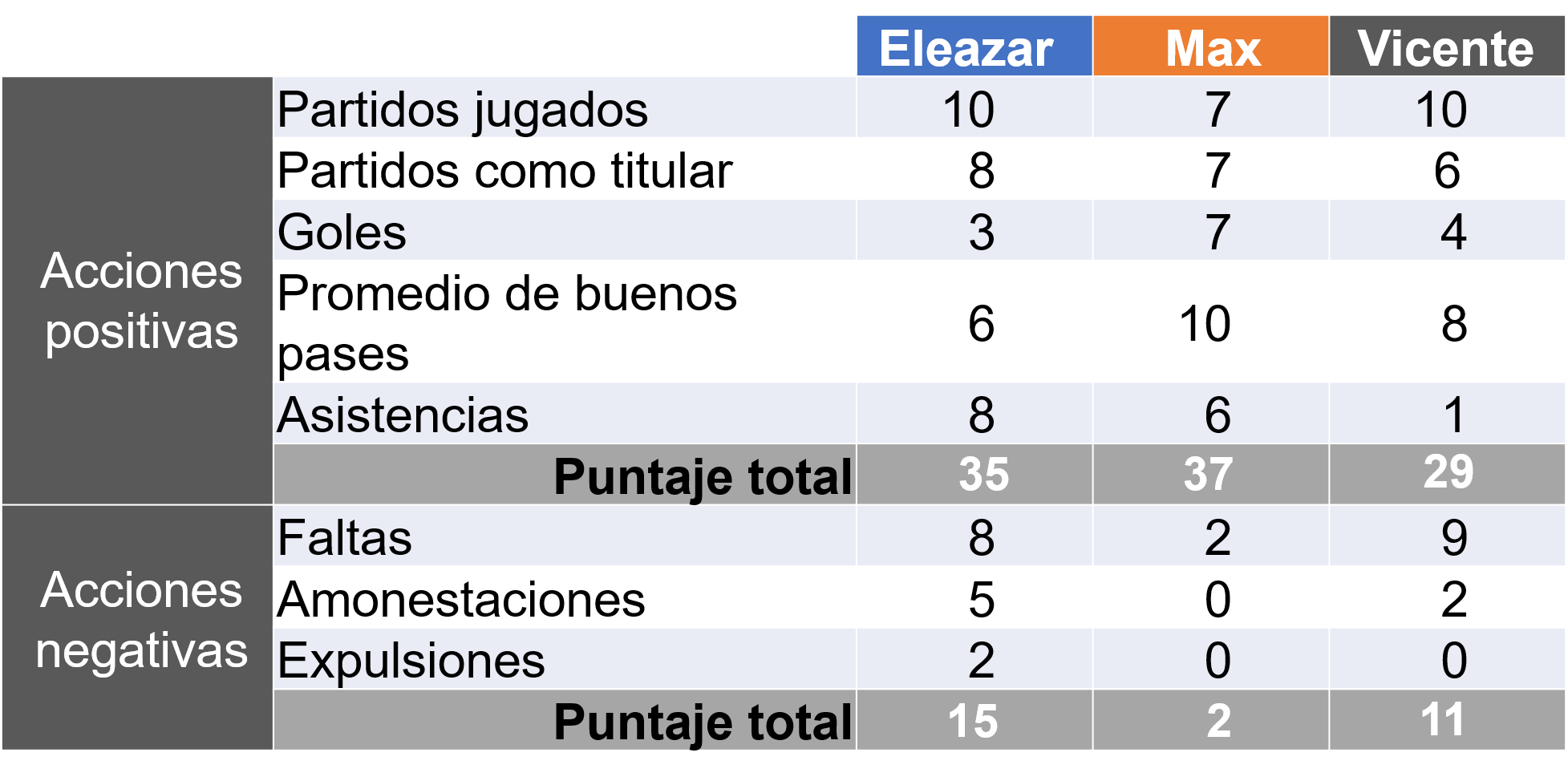
En otra tabla se organizan los resultados anteriores de cada jugador para calcular los porcentajes correspondientes a cada categoría, así como el ángulo para cada sección de la gráfica circular.
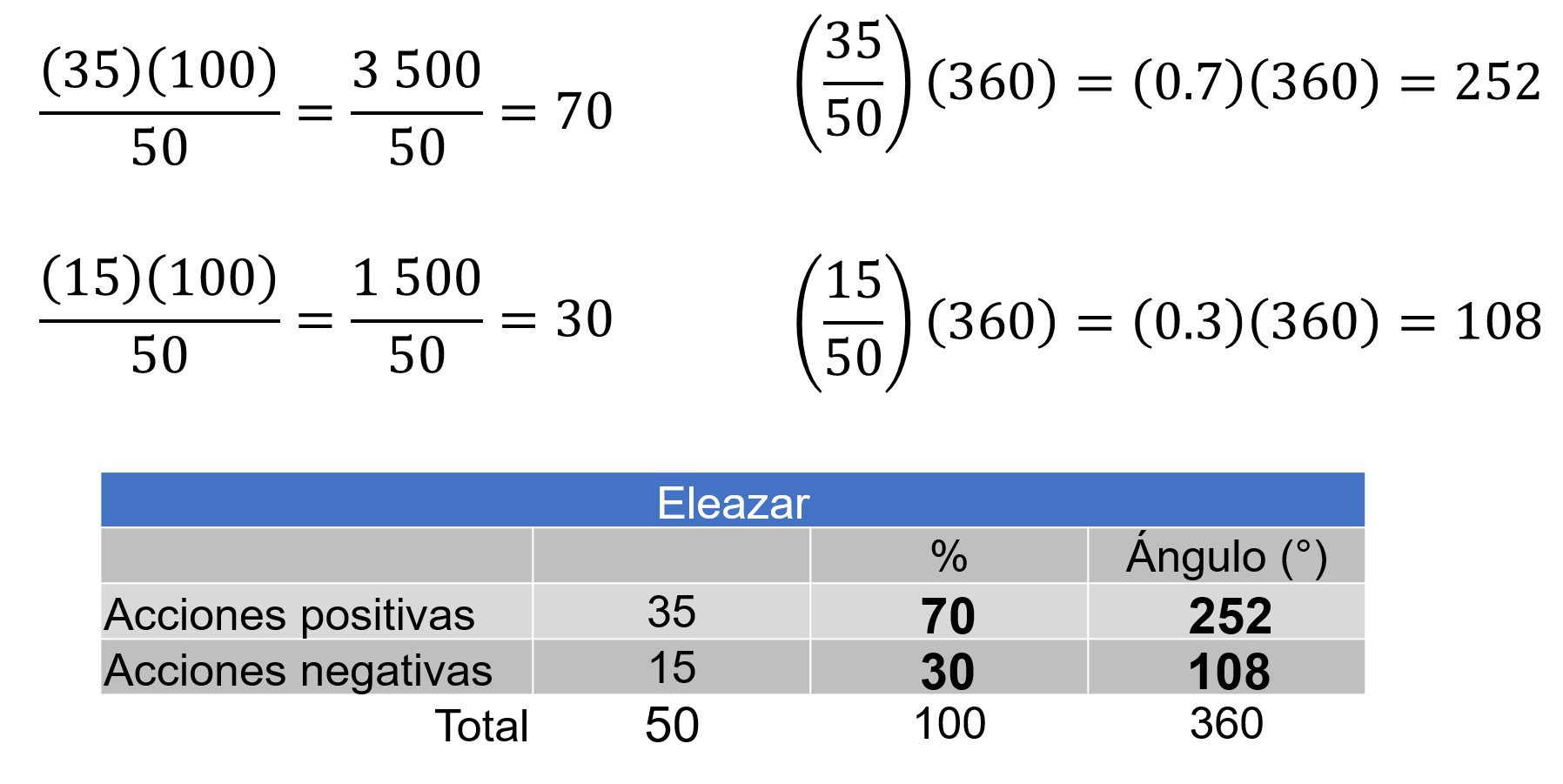
Para Eleazar, el total que es 50 puntos, para calcular el promedio.
Se multiplica 35 por 100, igual a 3500, se divide entre 50, el resultado es 70 por ciento.
Para las acciones negativas es 15 por 100, se obtiene 1500, se divide entre 50 y el porcentaje es 30 por ciento.
Para calcular la abertura del ángulo. El sector circular es igual a 35 entre el total 50, se obtiene 0.7, se multiplica por 360 grados y la abertura del ángulo es de 252 grados.
Para calcular el sector circular correspondiente a 15, se divide entre 50, el resultado es 0.3 que, al multiplicarlo por 360 grados, el ángulo resultante es de 108 grados.
Para calcular los porcentajes de Max, se toma en cuenta su total igual a 40.
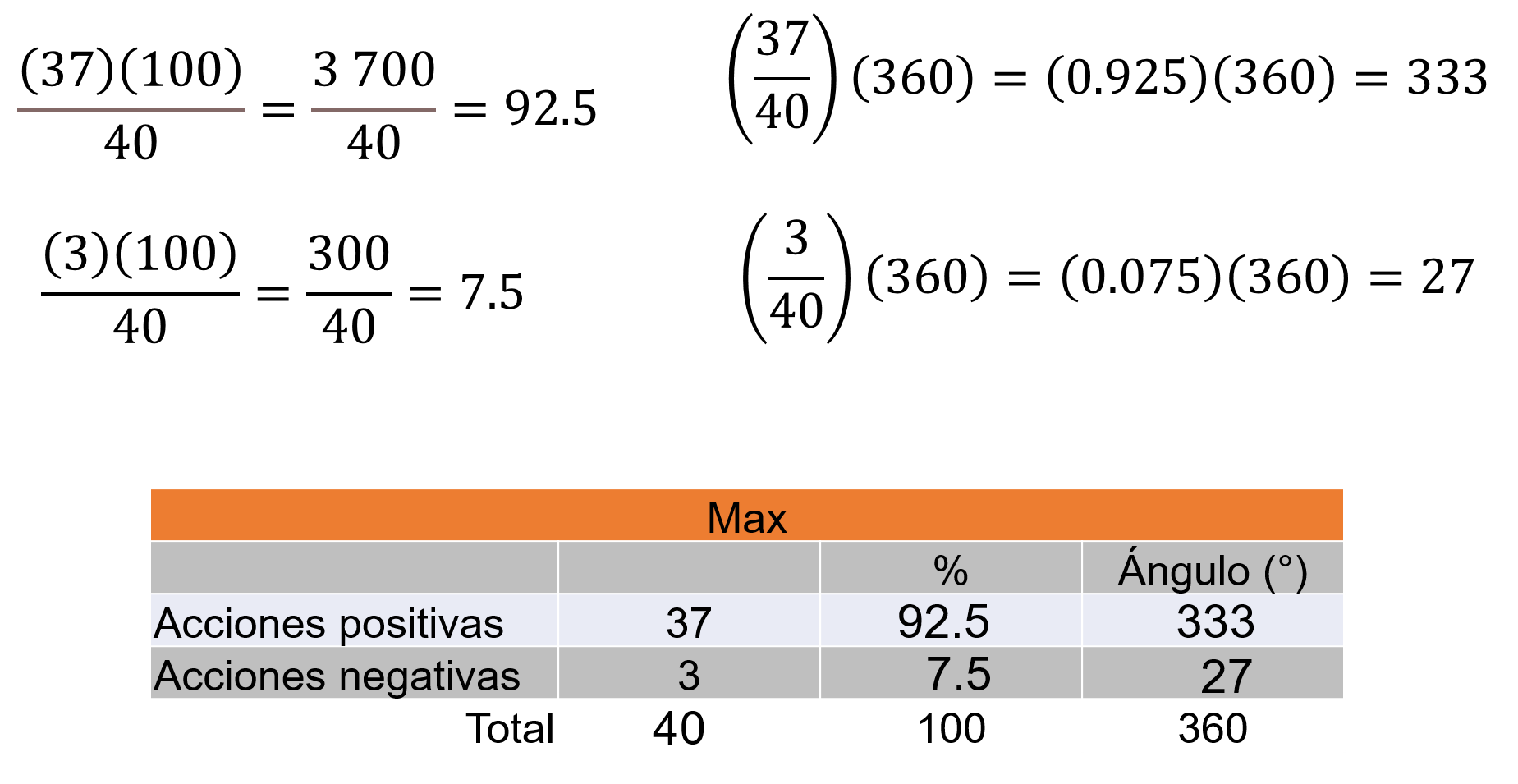
37 se multiplica por 100, igual a 3700, se divide entre 40 y el resultado es 92.5 por ciento.
Para 3, se multiplica por 100, se obtiene 300, se divide entre 40 y, el porcentaje es de 7.5 por ciento.
Para calcular los sectores circulares. De 37, se divide entre 40, su cociente es 0.925, multiplicado por 360 grados, el resultado es 333 grados.
Para 3, al dividirlo entre 40, el resultado es 0.075, al multiplicarlo por 360 grados el ángulo es 27 grados.
Es el turno de Vicente; calcula sus porcentajes y ángulos.
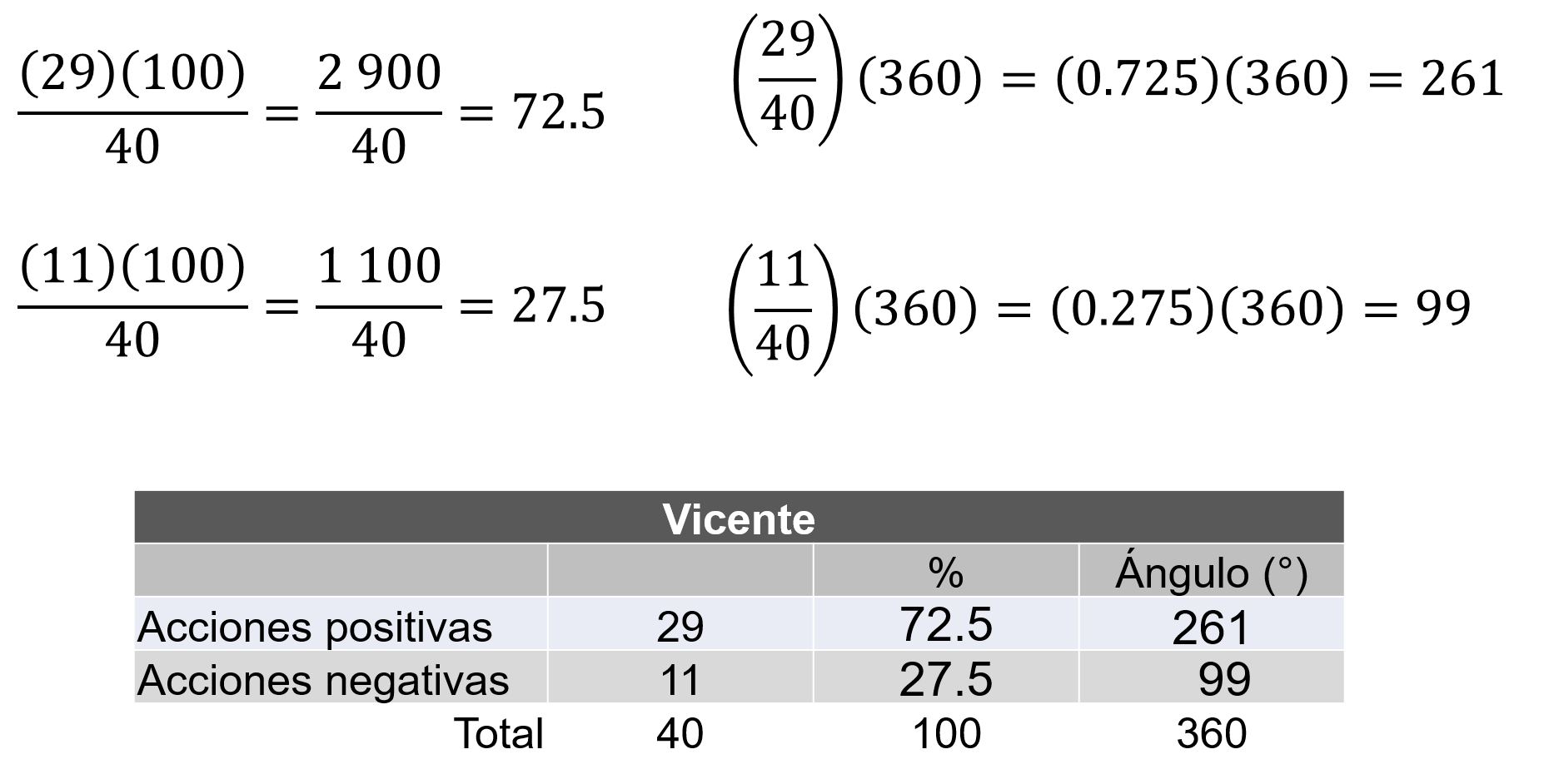
Acciones positivas 29, se multiplica por 100 y el resultado 2900, se divide entre 40, el porcentaje es 72.5 por ciento.
Acciones negativas 11, lo multiplicamos por 100, el resultado es 1100, se divide entre 40, por tanto, representa el 27.5 por ciento.
Para calcular los sectores circulares se divide 29 entre 40, se obtiene 0.725 y al multiplicarlo por 360 el resultado es 261 grados.
Por último, 11 entre 40, resulta 0.275 multiplicado por 360 dan 99 grados.
Para trazar las tres gráficas circulares, utiliza un transportador para marcar los ángulos y coloréalos del color que te guste para diferenciarlos.
Comienza con los trazos.
Para la gráfica circular de los datos de Eleazar.
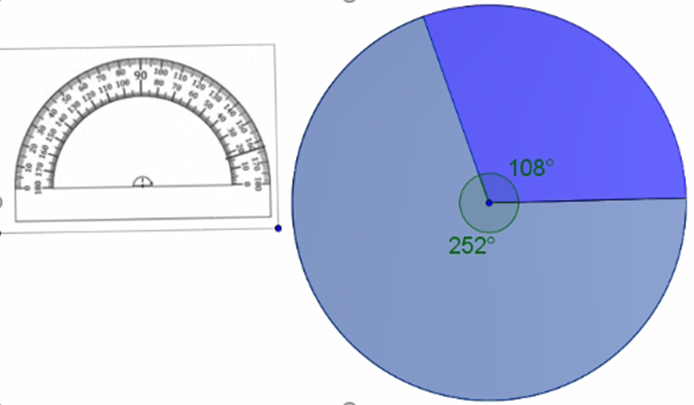
Traza una circunferencia de 5 cm de radio y el radio.
Ubica el transportador al centro de la circunferencia, alinea la graduación con respecto al radio.
Para facilitar los trazos midan el ángulo de 108 grados, y coloréalo a tu gusto.
Como son sólo dos ángulos, el ángulo de 252 grados es el sector que sobra, coloréalo de distinto color.
Para la gráfica circular de Max se ocupa el ángulo de 27 grados.
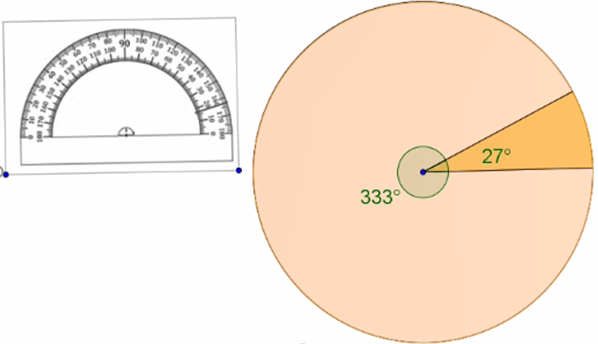
A partir de una circunferencia de 5 cm de radio, ubica el transportador al centro de la circunferencia, alinea la graduación con respecto al radio.
Mide el ángulo de 27 grados, y coloréalo a tu gusto.
Como son sólo dos ángulos, el ángulo de 333 grados es el sector que sobra, coloréalo de distinto color.
Por último, con los datos de Vicente, traza la gráfica circular.
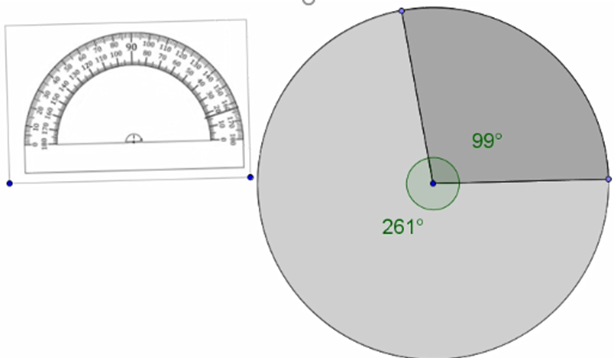
A partir de trazar una circunferencia de 5 cm de radio y el radio.
Ubica el transportador al centro de la circunferencia, alinea la graduación con respecto al radio.
Para facilitar los trazos midan el ángulo de 99 grados y coloréalo a tu gusto.
Como sólo son dos ángulos, el ángulo de 261 grados es el sector que sobra, coloréalo de distinto color.
Alumnas y alumnos, se tiene el histograma y las tres gráficas circulares que representan el desempeño de los tres jugadores.
A partir de la información mostrada por las gráficas, en tu cuaderno responde las siguientes preguntas.
¿Con cuál de las gráficas se facilita más la lectura para tomar la decisión sobre “el mejor jugador de la temporada”?
De acuerdo con las gráficas, ¿qué jugador consideran es el mejor?
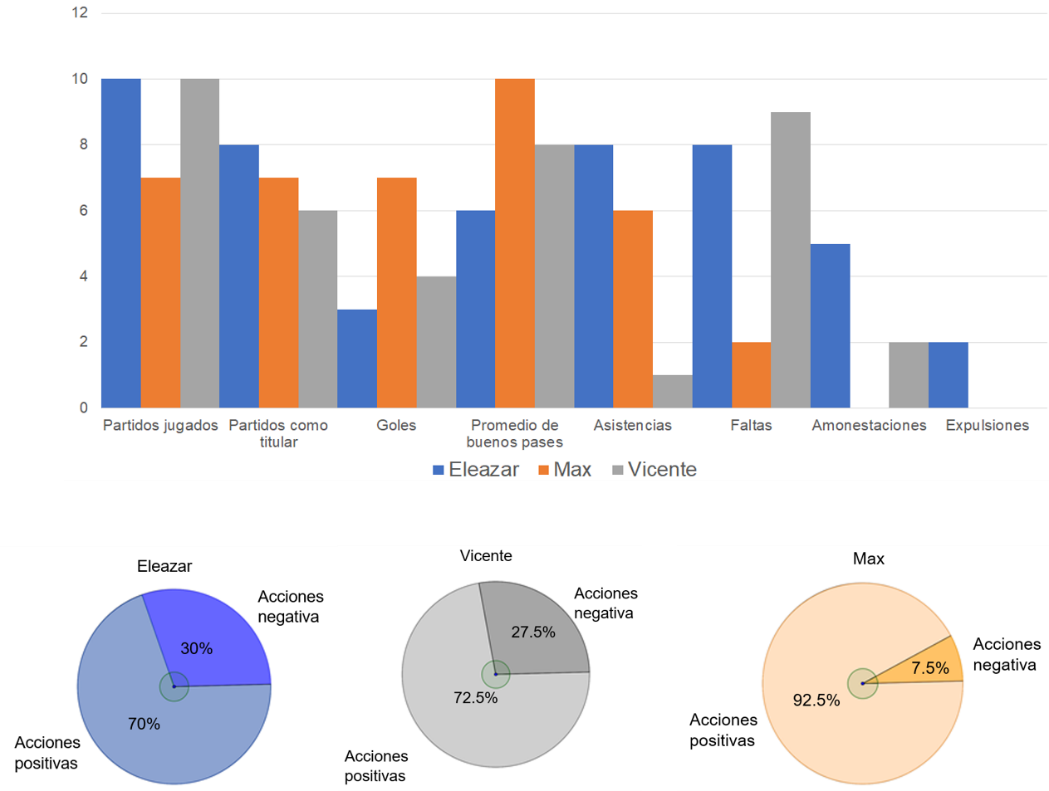
La gráfica que facilita observar la información del desempeño de los tres jugadores es la gráfica circular y así tomar una decisión.
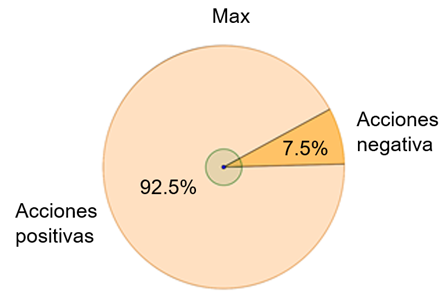
Así que ya puedes ayudar a Bernardo. El jugador que tiene mejor desempeño es Max.
El reto de hoy:
Si tienes dudas o quieres ejercitar lo aprendido, te puedes apoyar en tu libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.
