Estadística
Estadística
Aprendizaje esperado: compara la tendencia central (media, mediana y moda) y la dispersión (rango y desviación media) de dos conjuntos de datos.
Énfasis: conocer el desarrollo de la estadística.
¿Qué vamos a aprender?
Se te pide tener a la mano tu cuaderno, lápiz y una goma.
Anota en tu cuaderno cualquier idea o inquietud que surja al resolver las situaciones que aprenderás.
¿Qué hacemos?
¿Sabías qué? La práctica de la estadística se ejerce desde los grandes imperios del mundo antiguo. Por ejemplo, se han descubierto tablillas de arcilla de la civilización babilónica, que datan del año 5 000 antes de nuestra era.
Es por esta razón que las tabillas que están escritas en notación sexagesimal, enlistan personas, bienes y cantidades de alimentos traídos como ofrendas.
Después, desde Egipto, en la época de los faraones, se dedicaron a registrar datos con puntual exactitud, listas de familias, soldados, casas, jefes de familia y profesiones.
Asimismo, existen documentos del siglo VI antes de nuestra era del que se tiene registro sobre la obligación para la declaración de impuestos cada año, bajo pena de muerte, y basados en su profesión y sus fuentes de ingreso.
Por otra parte, la civilización china tenía como tradición realizar el censo de tierras y gente, bajo la diligencia del emperador Yu, en el año 2 238 antes de nuestra era.

En India, en el siglo IV antes de nuestra era, se publicó un tratado de ciencia política y economía, el Artha-shastra -que se deriva de las palabras “sastra”, ciencia, y “artha”, ganancia-; su autor, Kautilya, le sugería al rey un método para aumentar su poder y su riqueza, recomendando así un gobierno centralizado del que pudiera distribuir el poder en su reinado.
Mientras que en Grecia fueron famosos los métodos usados por Jerjes para contar a sus soldados, a quienes les ordenaba acomodarse en un recinto muy estrecho, con un total que superaba los 10 000 soldados.
También se sabe que en el año 310 antes de nuestra era, se efectuaba un censo bajo el reinado de Demetrio, contando con una población de 120 000 personas libres y 400 000 esclavos.

Y quienes eran muy buenos administradores y precisaban en los mejores censos cada cinco años, fue la civilización romana.
Todo ciudadano tenía como obligación el declarar su fortuna, y al igual que los egipcios, registraban su edad, nombre de la esposa, hijos, entre otros, para que, finalizado el conteo, se realizara una ceremonia religiosa, el Lustrum Conditum, palabras en latín de las que se deriva el concepto de lustro, un término de 5 años.
En el continente de América, los incas desarrollaron un sistema de estadística muy perfeccionado. Todos los datos relacionados con las actividades económicas y demográficas se conservaban en los “quipus”, unas cuerdas gruesas de las que colgaban varios hilos de distintos colores, según el objeto que representaban, amarillo para las piezas de oro, rojo para los soldados, blanco para las construcciones, entre otras.

En los hilos se hacían nudos para representar distintas cantidades; en la parte inferior, los nudos indicaban unidades, después las decenas, más arriba las centenas, y así sucesivamente, hasta las 10 000 unidades.
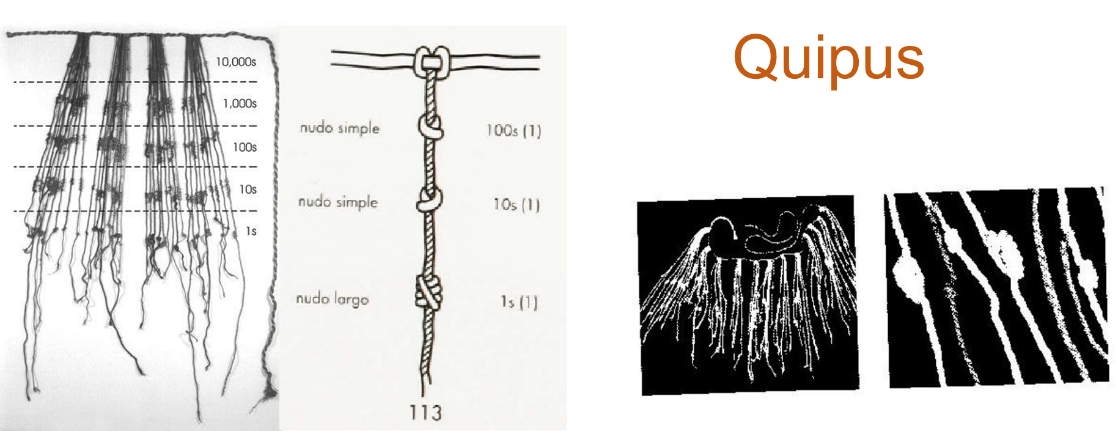
El uso de los quipus estaba reservado a los iniciados y hasta la fecha, no se han aclarado todas sus características.
Pero la estadística da un gran salto cualitativo a mediados del siglo XVII.
Por un lado, los datos estadísticos empiezan a ser empleados por los bancos y las nacientes compañías de seguros, y por otro, se inventa en Inglaterra el concepto de “Aritmética Política” y se empiezan a “matematizar” otras disciplinas que eran, hasta entonces, puramente descriptivas. Ejemplos tales como la demografía, economía y las ciencias sociales, que a su vez se transforman al contacto con las matemáticas.
Otro acontecimiento que dio a la estadística su justificación teórica y sus métodos fue el progreso del cálculo de probabilidades, ya que ambas permiten estudiar problemas donde intervienen fenómenos aleatorios.
Siendo así que, en la actualidad, la estadística junto con el cálculo de probabilidades, constituyen una rama independiente de las matemáticas con aplicaciones en casi todas las actividades humanas, física, astronomía, biología, genética, medicina, agricultura, sociología, entre otras. En cada ciencia se hacen predicciones, encuestas, controles de calidad y otras actividades que favorecen el estudio en cada una.
Y así también se aplican los métodos de la estadística al estudio de fenómenos “no medibles” en disciplinas como la lingüística y la literatura.
Con en el siguiente audiovisual se puede comprobar cómo se utiliza la estadista en la actualidad, incluso sin que te des cuenta.
- La Estadística
Observa los principales resultados de la estadística usados en la educación básica.
Actualmente la probabilidad -incluidos los temas clásicos de la estadística-, tienen una importancia cada vez mayor tanto en las ciencias como en las técnicas.
Porque cada vez más se recurre a la probabilidad y estadística para recolectar, organizar, resumir, presentar y analizar datos, así como para obtener conclusiones válidas, hacer inferencias y tomar decisiones con base en el análisis.
Durante el resumen histórico del surgimiento de la estadística se observa que la sociedad genera a ritmo creciente una gran cantidad de datos presentados por medio de porcentajes, tasas e índices, o bien, en forma de tablas, gráficas e inferencias estadísticas.

Esta información se transforma en conocimiento válido para ser comprendida y permitir una toma de decisiones racional. Para ello, el manejo de cifras, la extracción de información de una tabla, la interpretación de gráficas y la evaluación crítica de argumentos basados en estadísticas, como en los resultados de una encuesta, por mencionar alguno, son habilidades cada vez más necesarias desde temprana edad.
Es decir, las ideas básicas de la estadística son accesibles y pueden dar lugar a actividades interesantes para los estudiantes y, al mismo tiempo, reforzar el aprendizaje de otras partes de las matemáticas.
Y en el caso de la educación secundaria, ¿qué se espera sobre el análisis de datos?
La progresión de los aprendizajes esperados del eje “Análisis de datos” que se rige por cuatro ideas fundamentales.
Uno. Reconocer la importancia de los datos para entender los fenómenos naturales y sociales.
Dos. Hacer uso de las distribuciones y sus representaciones, ya sean tablas o gráficas, como recursos para comprender los datos obtenidos.
Tres. Usar e interpretar las medidas de tendencia central y de dispersión para reducir la complejidad de los conjuntos de datos y así aumentar las posibilidades de operar con ellos.
Y cuatro. Emplear el estudio de la probabilidad como método para tratar con la incertidumbre, que significa contar con métodos para medir la incertidumbre implícita en el uso de la estadística.
Revisa la siguiente situación.
Situación 1. Se realiza un experimento para conocer cuál de dos marcas de pasta dental es la preferida del público. Se tiene que, de un total de 20 personas, decidieron así, 14 eligieron la marca “x” y 6 la marca “y”.

Se deben responder dos cuestiones.
a) Estos resultados, ¿son suficientes para afirmar que las personas prefieren la marca “x”?
b) En un experimento como el anterior, aun siendo igual la preferencia por las dos marcas, ¿cuál es la probabilidad de que haya 14 o más personas que prefieran una marca sobre otra?
¿Qué se debe realizar primero?
Para simular la situación, las alumnas y los alumnos pueden convenir —suponiendo la misma preferencia por ambos productos—, que el experimento es equivalente a lanzar 20 veces una moneda y observar las frecuencias de los resultados entre águila y Sol.
Entonces, al realizar varias veces el experimento, se puede encontrar que alrededor de 25% de las veces se obtienen más de 14 lanzamientos en águila o más de 14 en Sol.
Esto significa que las veces que se repita el experimento, aproximadamente una de cada cuatro se va a encontrar una preferencia acentuada por una de las marcas, sea la “x” o la marca “y”.
Por lo tanto —a pesar de la aparente desproporción entre el número de personas que prefirieron cada marca—, los datos proporcionados constituyen una base muy endeble para asegurar la preferencia de la marca “x”, ya que puede ser el resultado de la casualidad.
Cabe señalar que actividades como esta introducen gradualmente a las alumnas y a alumnos a las nociones de la estadística, y los ayudan a comprender la existencia de problemas que no pueden resolverse mediante una única observación o medición.
Entonces, luego de recopilar y organizar gran cantidad de datos, pueden obtenerse repuestas parciales a cuestiones como:
¿Cuáles son los datos que aparecen con mayor frecuencia y cuáles casi no aparecen?
¿Qué tendencias revelan estos datos?; ¿cuál es su significado y cómo se interpretan?, y ¿hay otras interpretaciones posibles?
O quizás, ¿puede generalizarse a grupos más grandes?, ¿a cuáles otros grupos?
¿Y qué tipo de estudios adicionales pueden hacerse para confirmar o refutar las interpretaciones?
Estos cuestionamientos son acertados, aunque algunas preguntas exigen un grado más alto para resolverse.
Por ello, es importante que los resultados obtenidos a partir de un estudio estadístico puedan estimular la discusión y así, aprender a realizar argumentaciones basadas en datos.
Es decir, que los contenidos de estadística de los programas de educación secundaria, más que intentar abarcar un amplio repertorio de definiciones, fórmulas y procedimientos, están centrados en un conjunto pequeño de ideas fundamentales.
Entonces ¿cuáles son los conceptos sobre estadística para secundaria?
En el caso de la educación secundaria se analizan tanto las medidas de tendencia central como de dispersión.
Las medidas de tendencia central son medidas estadísticas las cuales sintetizan los datos en un valor representativo.
También son un apoyo para calcular otros parámetros estadísticos.
Las medidas de tendencia central más utilizadas son:
– Media aritmética, también conocida como promedio;
– Mediana, y
– Moda.
Las medidas de dispersión en cambio miden el grado de dispersión de los valores de la variable.
Dicho, en otros términos, las medidas de dispersión indican qué tan separados o cercanos están los datos con respecto a la media aritmética, así como la amplitud del conjunto de valores.
Las medidas de dispersión más utilizadas son rango y desviación estándar.
En estadística hay dos tipos de datos con los cuales se trabajan para calcular las medidas estadísticas.
Una vez realizada la recolección de datos, por ejemplo, de una encuesta, los datos en su forma original son considerados datos “no agrupados”, así como cuando se tiene una muestra de menos de 30 datos no es necesario formar clases o agrupaciones, por lo tanto, se trabaja con ellos como datos “no agrupados”.
Pero cuando se tiene un conjunto de datos mayor a 30 es recomendable organizar y clasificar la información bajo ciertas características, es decir, agruparlos para formar “clases”. A éstos se les da un tratamiento como “datos agrupados”.
Pero ¿a qué se refiere la media aritmética o promedio?
La media aritmética o promedio se define como la suma de todos los datos dividida entre el número total de los mismos.
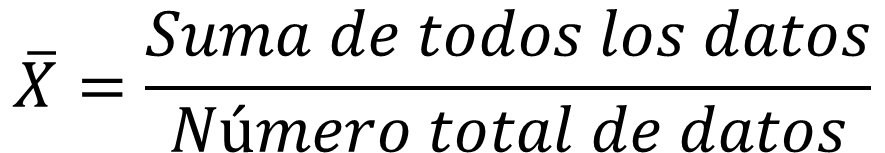
La media aritmética es el valor promedio de las muestras.
Revisa ¿cuál es la media aritmética de los siguientes datos?
6, 7, 8, 8, 10
Al sumar 6 más 7 más 8 más 8 más 10 se obtiene como resultado 39, entre el número total de datos, es decir, 5; por lo tanto, la media aritmética de este conjunto de datos es igual a 7.8.
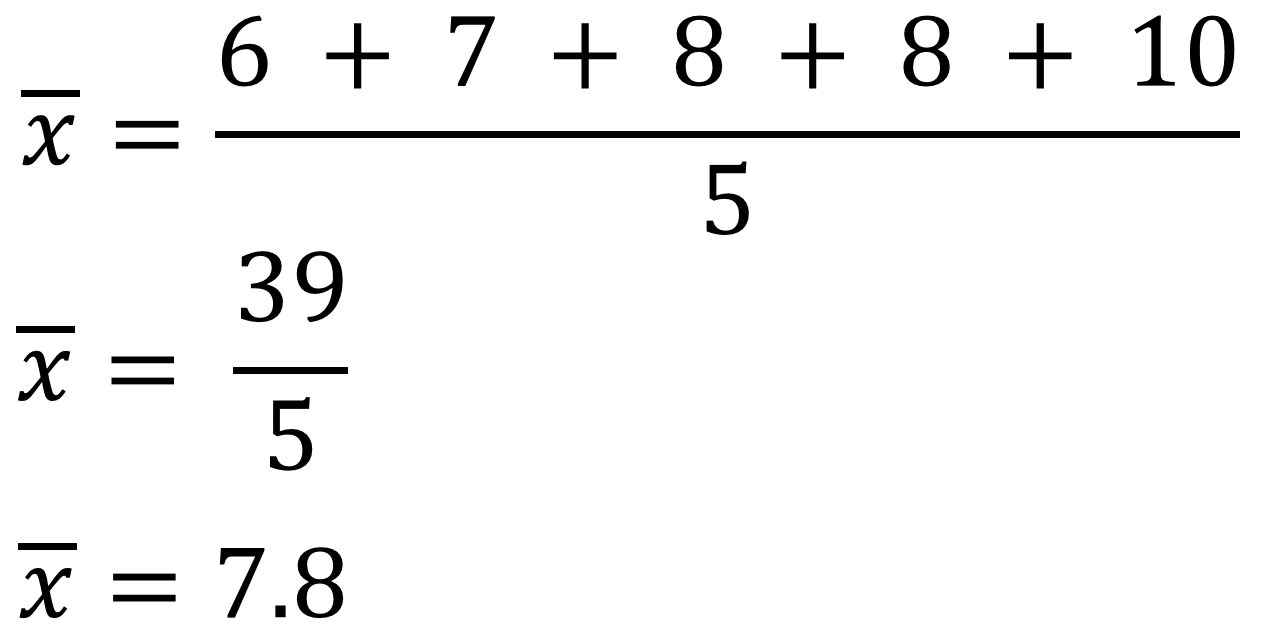
¿Y en cuanto a la mediana?

Es decir, el 50% de los datos tienen valores iguales o inferiores a la mediana y el otro 50% tiene valores iguales o superiores a la mediana.
Si el número de datos en el conjunto es par, la mediana corresponde al promedio de los dos valores centrales.
Por ejemplo, en la muestra 3, 9, 11, 15, la mediana es igual a 9 más 11, entre 2, cuyo resultado es igual a 10.
Cuando el número de datos en el conjunto es impar, la mediana corresponde al dato central.
Por ejemplo, en el caso del conjunto 5, 7, 9, 11, 13, el valor central es 9 dado que hay dos valores a su izquierda y dos valores a su derecha; entonces la mediana es igual a 9.
¿Cuál es la moda?
La moda de una medida de distribución la cual se define como el valor de la variable que más se repite.
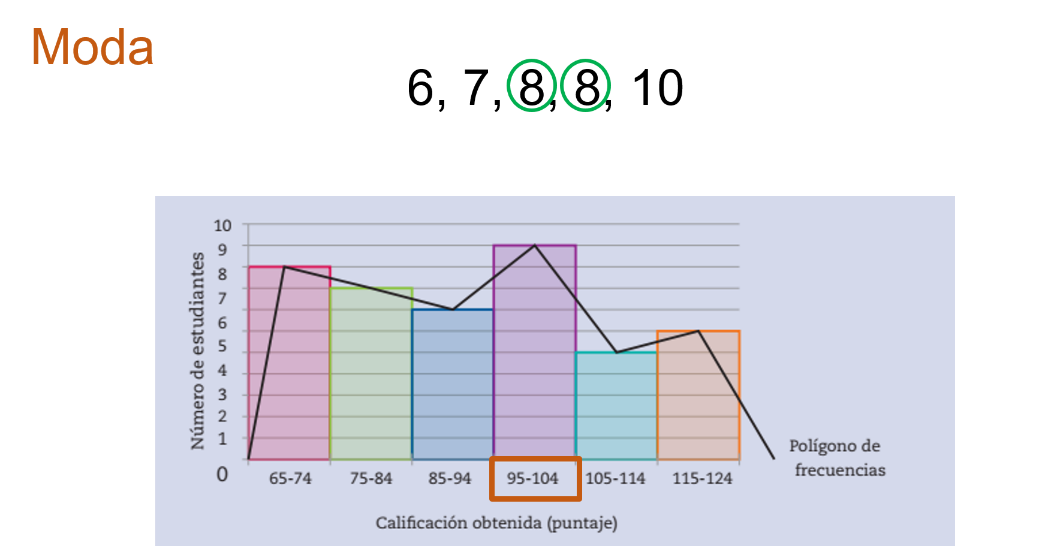
Por ejemplo, para el conjunto de datos 6, 7, 8, 8, 10, la moda es 8.
En este caso en el polígono de frecuencia, la moda corresponde al valor de la variable ubicado debajo del punto más alto de la gráfica.
Cabe señalar que, una muestra puede tener más de una moda, por ejemplo, en la siguiente tabla hay tres clases de edades con la mayor frecuencia.
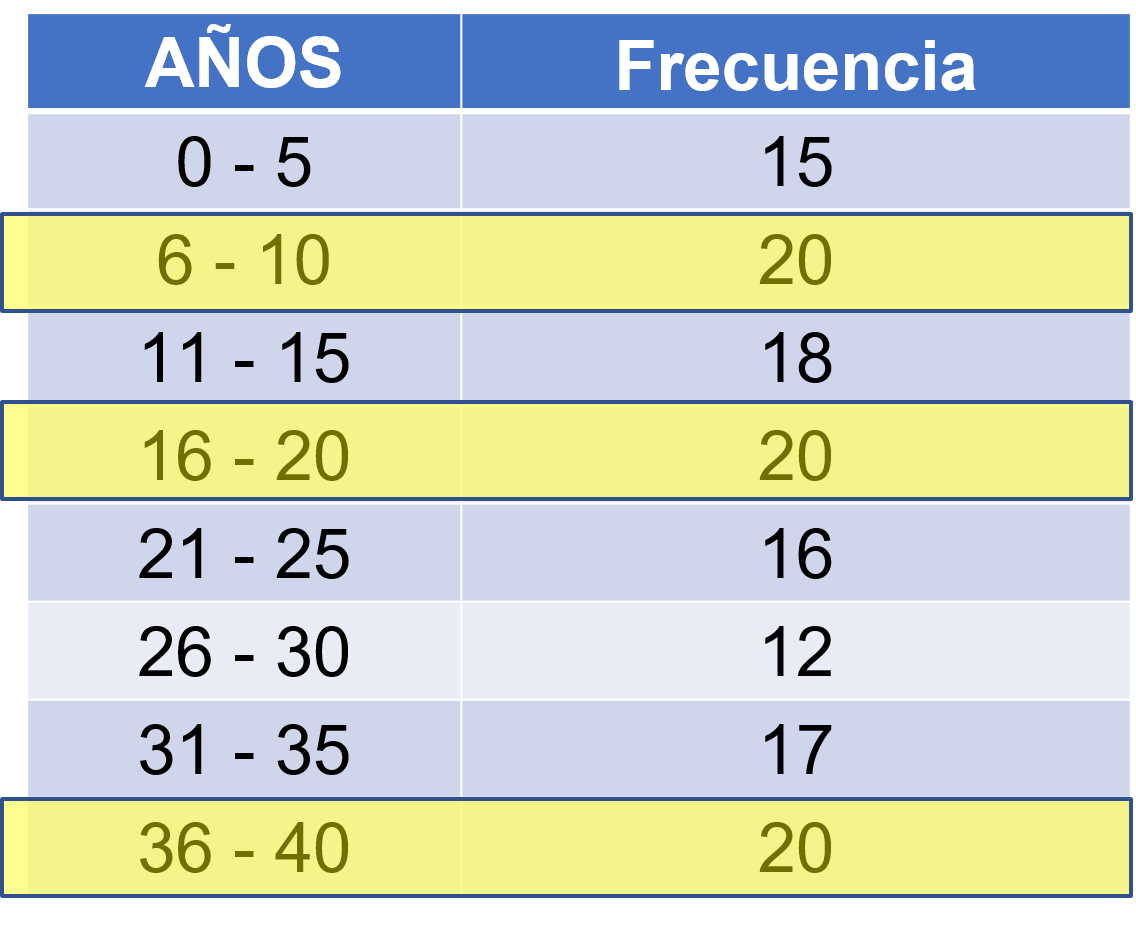
Ahora bien, observa las medidas de dispersión mencionadas con anterioridad.
¿En qué consisten las medidas de dispersión?
Las medidas de dispersión miden el grado de dispersión de los valores de la variable.
¿En qué consiste el rango?
El rango se define como la diferencia entre el dato mayor y el dato menor.

Un ejemplo son los siguientes datos.
Como el dato de mayor valor es 45 y el dato de menor valor es 16, al realizar la resta, el rango es 29.

¿En qué consiste la desviación estándar?
La desviación estándar es la medida de dispersión más común. Ésta indica qué tan dispersos están los datos con respecto a la media aritmética.
Mientras mayor sea la desviación estándar, mayor será la dispersión de los datos.
Recapitula.
Al trabajar con el aprendizaje esperado “Calcula y explica el significado del rango y la desviación media”.
Analizaste el resumen histórico del surgimiento del estudio de la estadística.
Y finalmente, analizaste las medias de tendencia central y las principales medidas de dispersión estudiadas en la educación básica.
El reto de hoy:
Reflexiona sobre el resumen histórico del surgimiento del estudio de la estadística hasta cómo es en la actualidad.
Tu libro de texto de Matemáticas de tercer grado tiene ejercicios similares para analizar los principales resultados de la estadística. Es importante que practiques lo aprendido.
Leonardo Da Vinci dijo: “Ninguna investigación humana puede ser denominada ciencia si no pasa a través de pruebas matemáticas”.
¡Buen trabajo!
Gracias por tu esfuerzo.
