Medidas de tendencia central y de dispersión
Medidas de tendencia central y de dispersión
Aprendizaje esperado: compara la tendencia central (media, mediana y moda) y la dispersión (rango y desviación media) de dos conjuntos de datos.
Énfasis: dar sentido y significado a las medidas de tendencia central y de dispersión.
¿Qué vamos a aprender?
Los materiales que utilizarás son tu cuaderno de apuntes, bolígrafo, lápiz y goma.
Elabora tus propias notas o resumen con los datos importantes. También anota en tu cuaderno cualquier duda o inquietud que surja al resolver las situaciones de la sesión.
¿Qué hacemos?
La estadística es una rama de las matemáticas, la cual se encarga de recolectar, organizar, resumir, analizar, generalizar, presentar y comparar los resultados de estudios reales en la vida cotidiana para la toma de decisiones en las distintas áreas como la economía, los deportes, la salud, entre otras disciplinas.
Has calculado en diferentes situaciones las medidas de tendencia central, es decir, la media aritmética o promedio, moda y mediana.
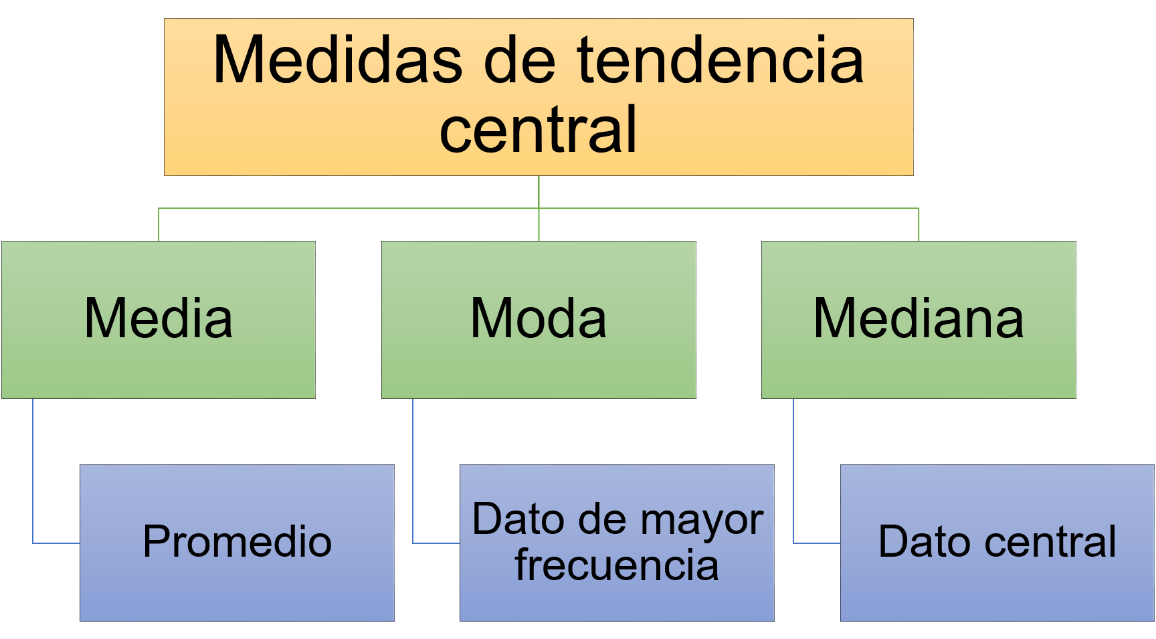
La media aritmética o promedio es la suma de un conjunto de datos dividido entre el número total de datos del conjunto.
La moda es el valor de mayor frecuencia en un conjunto de datos.
La mediana es el valor del elemento central de un conjunto de datos ordenados de menor a mayor, o en su defecto, el promedio de los dos valores centrales en el caso de un conjunto con número de datos par.
Pon en práctica las medidas de tendencia central en el siguiente ejercicio.
En una escuela secundaria, el maestro Juan, de matemáticas, aplicó un examen; las calificaciones obtenidas por los alumnos se muestran en el siguiente audiovisual, observa cómo se calculan las tres medidas de tendencia central y determina cuál de ellas representa mejor al conjunto de datos.
- Las medidas de tendencia central
https://www.youtube.com/watch?v=nmZhbUSvMfc
La medida de tendencia central más representativa, en este caso de las calificaciones, fue la mediana igual 7, porque más del 50% de los estudiantes obtuvieron 7 o más de calificación.
En el caso de las medidas de dispersión, éstas permiten conocer otras características sobre un conjunto de datos, como lo es la distancia entre los valores o la separación que existe entre ellos.
Las medidas de dispersión son:
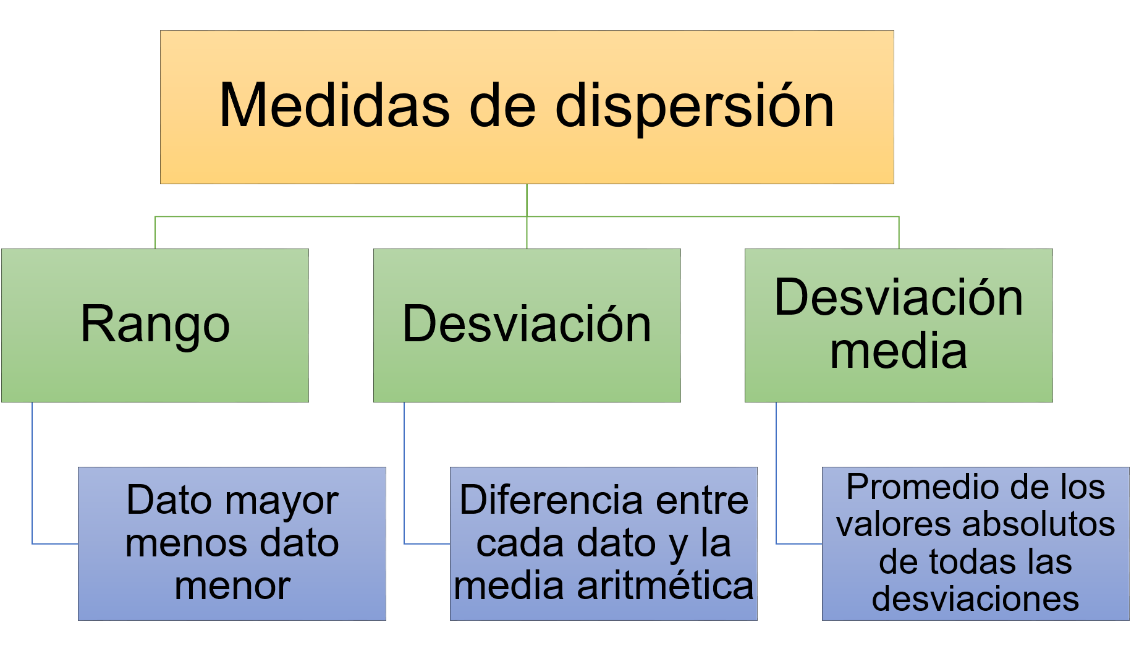
El rango, el cual se obtiene restando el dato de mayor valor al dato de menor valor en un conjunto de datos.
Desviación, es la diferencia entre cada dato y la media aritmética.
La desviación media, es el promedio de los valores absolutos de todas las desviaciones.
Pero surge una duda, sabes en qué consisten las medidas de dispersión, pero ¿cómo se aplican para interpretar los datos de un estudio estadístico?
Observa la siguiente situación es un estudio estadístico del petróleo en México.
En el año de 1972, un pescador, Rudesindo Cantarell, descubrió una mancha de aceite que brotaba de las profundidades del mar en la zona conocida como la Sonda de Campeche.

Poco tiempo después, quedó al descubierto que México había localizado un yacimiento petrolero gigante.
El apellido del descubridor le dio nombre al lugar, Cantarell.
Los primeros barriles de petróleo de Cantarell se produjeron en junio de 1979, con un promedio diario de 4 290 barriles.
El efecto Cantarell se hizo sentir rápidamente. Con base en los datos proporcionados por Pemex se sabe que:
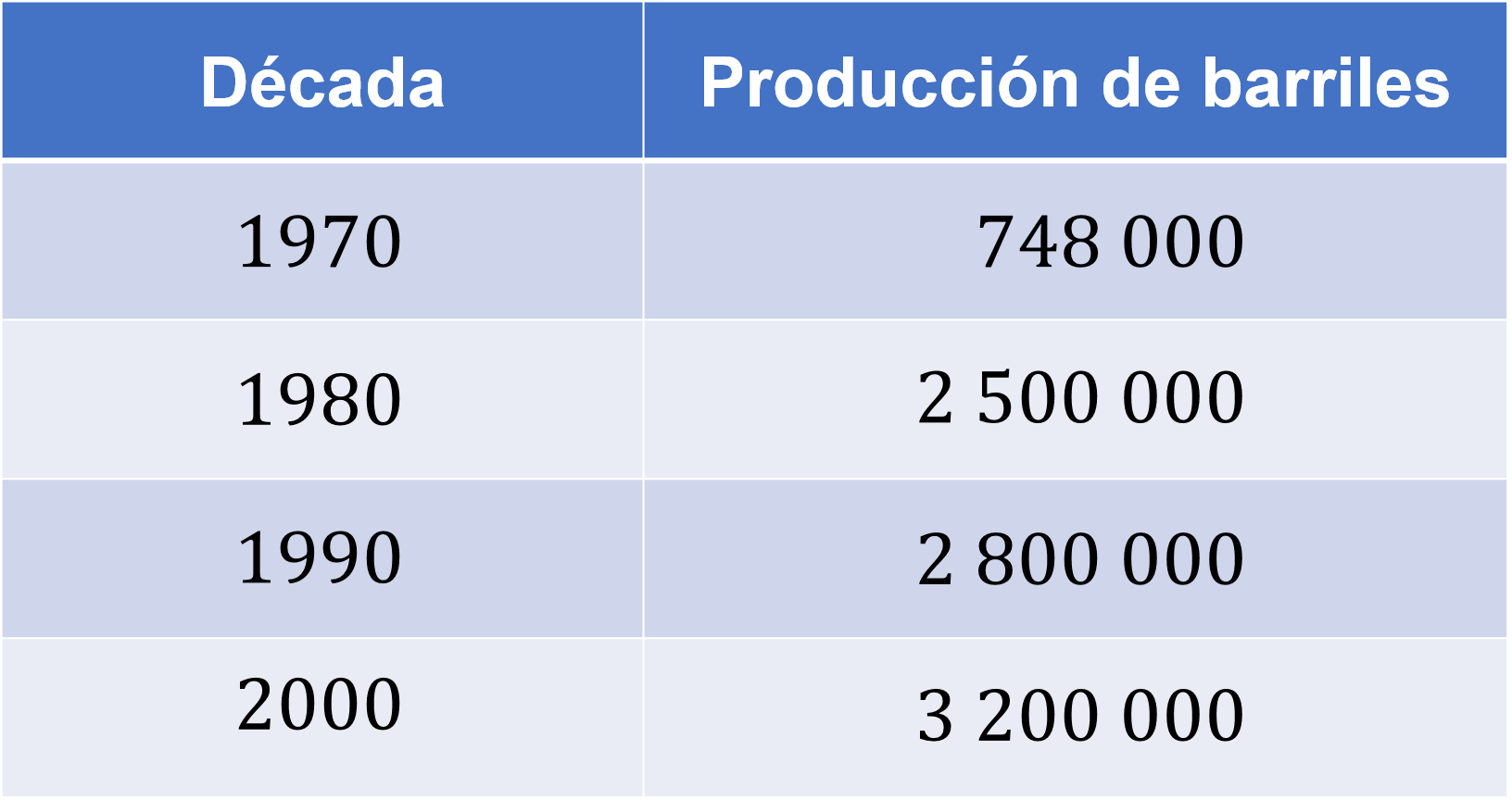
De producir 748 000 barriles diarios durante la década de 1970, el promedio de producción diaria del país creció hasta alcanzar 2.5 millones de barriles en la década de 1980, 2.8 millones en los noventa y 3.2 millones en los datos disponibles de la década correspondiente al año 2000.
Con base en la información presentada, ¿cuál es la media de producción de 1970 a los datos de la década de los 2000?
La media permite conocer el promedio de producción de petróleo entre la década de los 70 hasta la de los 2000.
Es decir, si se suman las producciones de barriles de los cuatro periodos, setecientos cuarenta y ocho mil, más dos millones quinientos mil, más dos millones ochocientos mil, más tres millones doscientos mil; todo dividido entre cuatro.
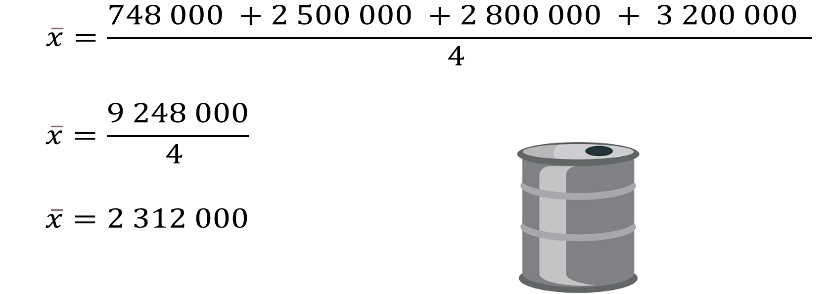
Al realizar las operaciones se tiene igual a nueve millones doscientos cuarenta y ocho mil, entre 4.
Por lo tanto, la media aproximada de producción de barriles entre las 4 décadas fue de dos millones trescientos doce mil barriles.
¿Qué dato muestra una desviación mayor respecto del promedio?
Para saber qué dato está más alejado de la media aritmética, se puede representar la información por medio de una tabla donde se muestre el año y la desviación de cada uno.
Esta medida de dispersión permite saber cuán alejados o cerca están los datos en relación con un valor central.
Para la década de los 70, la desviación es igual a la cantidad de barriles producidos menos el promedio de barriles.
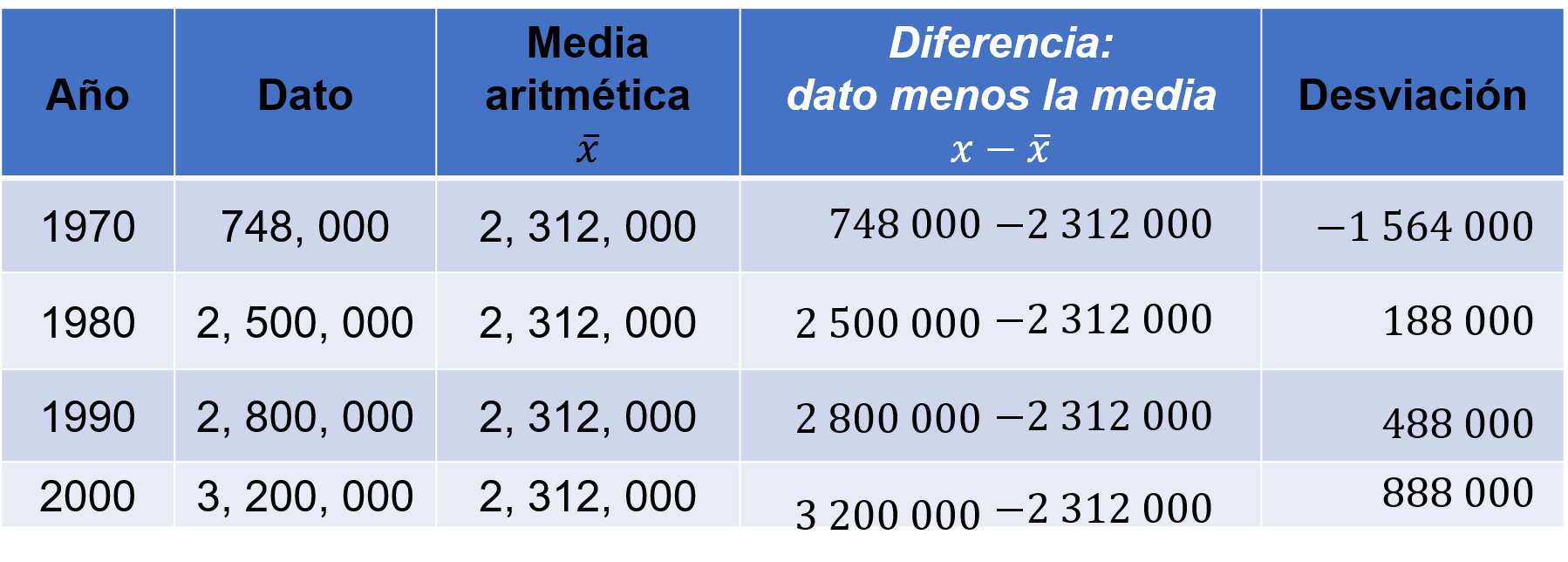
Es decir, setecientos cuarenta y ocho mil menos dos millones trescientos doce mil, es igual a un millón quinientos sesenta y cuatro mil negativo.
En los 80, la producción fue de dos millones quinientos mil menos la media de dos millones trescientos doce mil, entonces la desviación es igual a ciento ochenta y ocho mil.
En los 90, es igual a dos millones ochocientos mil barriles menos dos millones trescientos doce mil, es igual a cuatrocientos ochenta y ocho mil.
Y en la primera década del 2000, es igual a tres millones doscientos mil barriles, menos la media, es igual a ochocientos ochenta y ocho mil.
Se tiene un dato con una desviación negativa, ¿qué significa esto?
Imagina que se colocan los datos en una recta numérica, al centro está la media aritmética y las cantidades de producción de barriles cuya desviación es positiva están a la derecha de la media y, en el caso de la producción cuya desviación es negativa, está a la izquierda de la media.
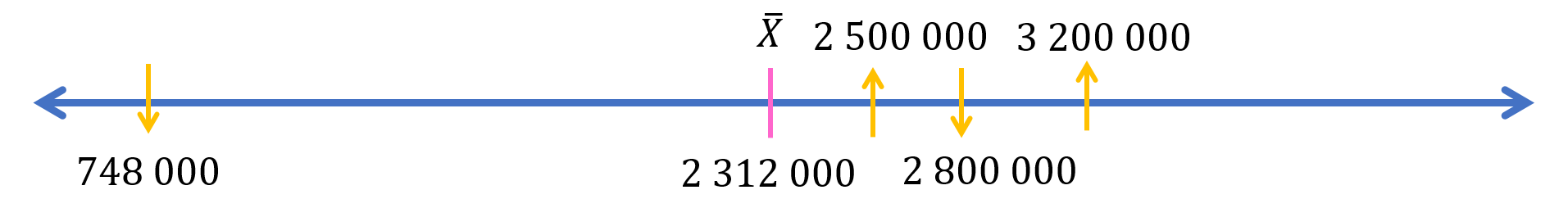
Por lo tanto, ¿qué dato muestra una desviación mayor respecto del promedio?
La producción de la década de los 70 es el dato con una desviación mayor respecto del promedio.
Ahora, analiza las siguientes preguntas.
¿Cuál es la media de producción de los 80 a la primera década del 2000? y ¿cuál es la desviación media de estos datos?
La media aritmética de la producción de los 80 a la primera década del 2000 es igual a dos millones quinientos mil, más dos millones ochocientos mil, más tres millones doscientos mil, todo entre 3. Igual a ocho millones quinientos mil entre tres.
Por lo tanto, la media de producción de 1980 a 2007 es igual a dos millones ochocientos treinta y tres mil trescientos treinta y tres, punto treinta y tres.

Ahora, la desviación media es igual a la suma de los valores absolutos de cada la desviación, todo entre tres, es decir, el total de datos.
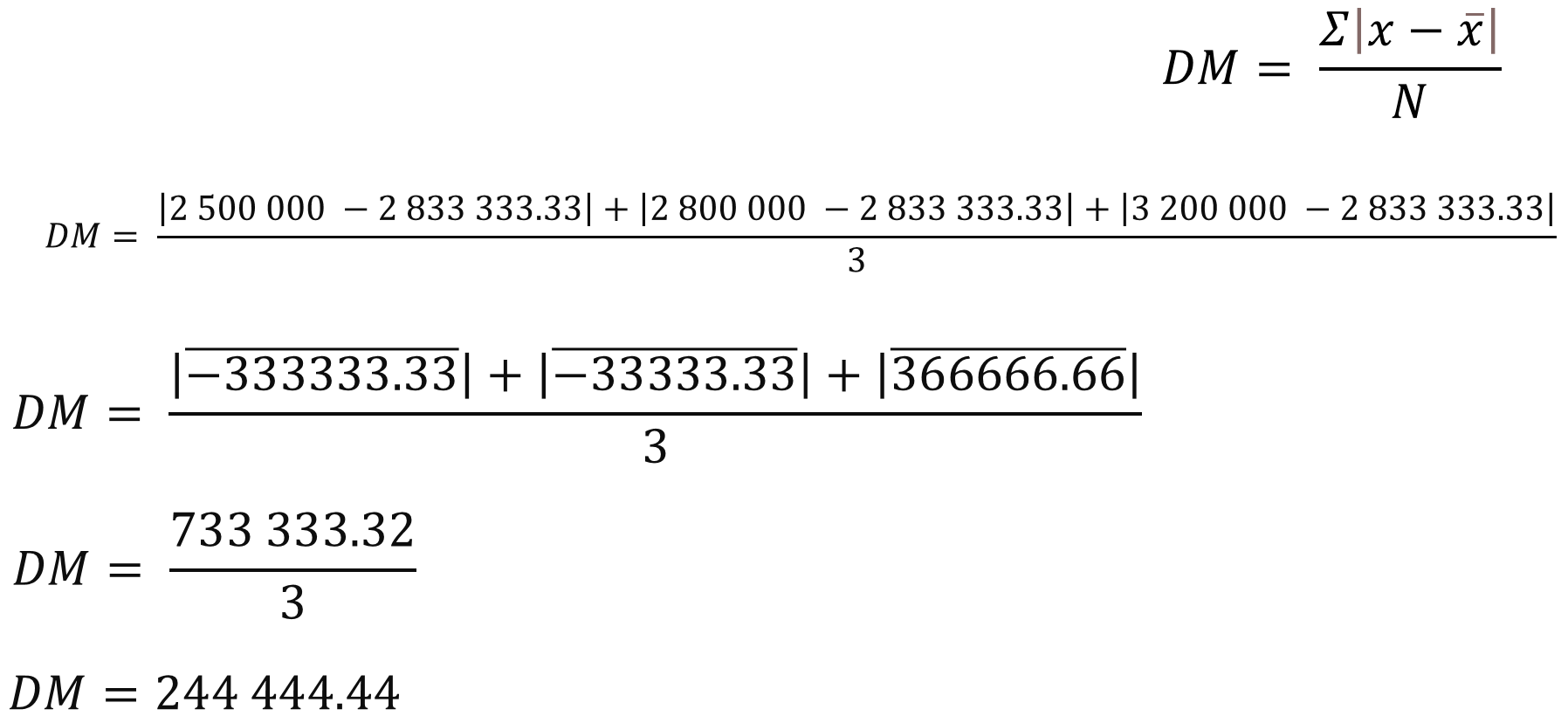
La cual es igual setecientos treinta y tres mil trescientos treinta y tres, punto treinta y dos, todo entre 3.
Por lo tanto, la desviación media es de doscientos cuarenta y cuatro mil cuatrocientos cuarenta y cuatro barriles de petróleo de la década de 1980 a la década del 2000.
¿Por qué varía tanto la media y la desviación media obtenidas?
Porque para la media aritmética recién calculada sólo se consideró el conjunto de datos de la producción en las décadas de 1980, 1990 y del 2000.
Faltando la cantidad de producción de barriles de petróleo de la década de 1970.
Observa y analiza la siguiente gráfica para responder algunas preguntas.
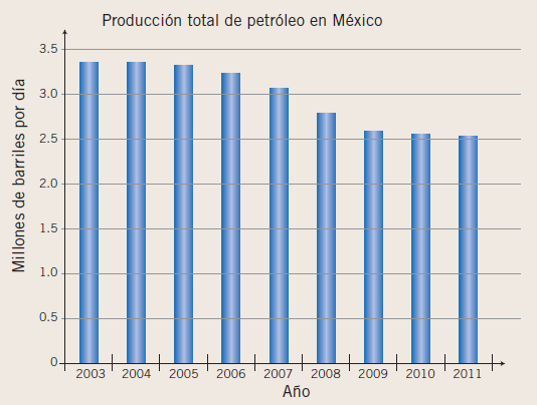
- ¿Qué información muestra la gráfica?
- ¿Cuál fue la media en la producción de petróleo en los años que muestra la gráfica?
- ¿En qué año la desviación respecto del promedio es mayor? ¿En cuál es menor?
e) ¿Cuál es la desviación media de los datos de la gráfica?
En la gráfica se muestra la producción anual de petróleo en México del año 2003 al año 2011 en millones de barriles por día.
¿Cuál es la media de esta producción?
La media es el promedio de los datos de producción de petróleo.
Es decir, 3.3 millones, más 3.3. millones, más 3. 3 millones, más 3.2 millones, más 3.1 millones, más 2.7 millones, más 2.6 millones, más 2.5 millones, más 2.5 millones, todo entre 9 que es el total de datos.
Igual a 26.5 entre 9, por lo tanto, el promedio de los datos de producción de petróleo por día es igual a 2.94 millones de barriles por día.
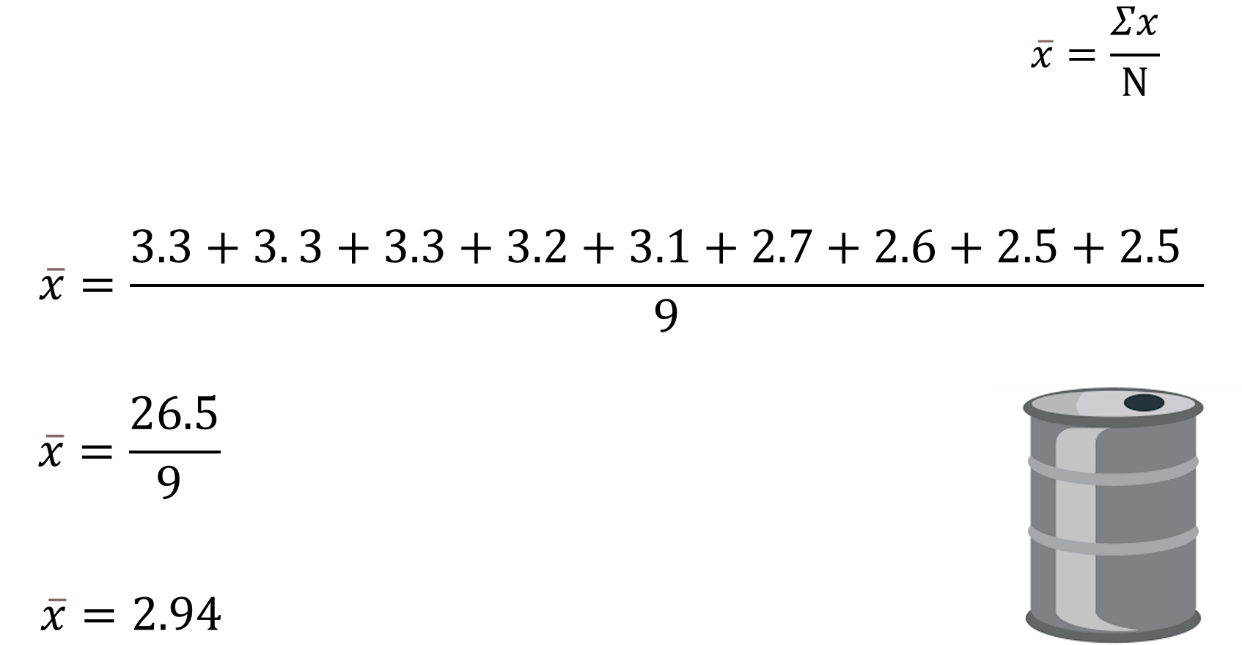
Con los datos de la gráfica y la media aritmética calculada es posible determinar la desviación y la desviación media de los datos de la producción de petróleo en México del año 2003 al año 2011.
Para conocer en qué año es mayor y menor la desviación, se organiza una tabla con el año, la producción de barriles de petróleo, la diferencia del dato menos la media y la desviación de cada dato con respecto a la media.
Observa y analiza la siguiente tabla.
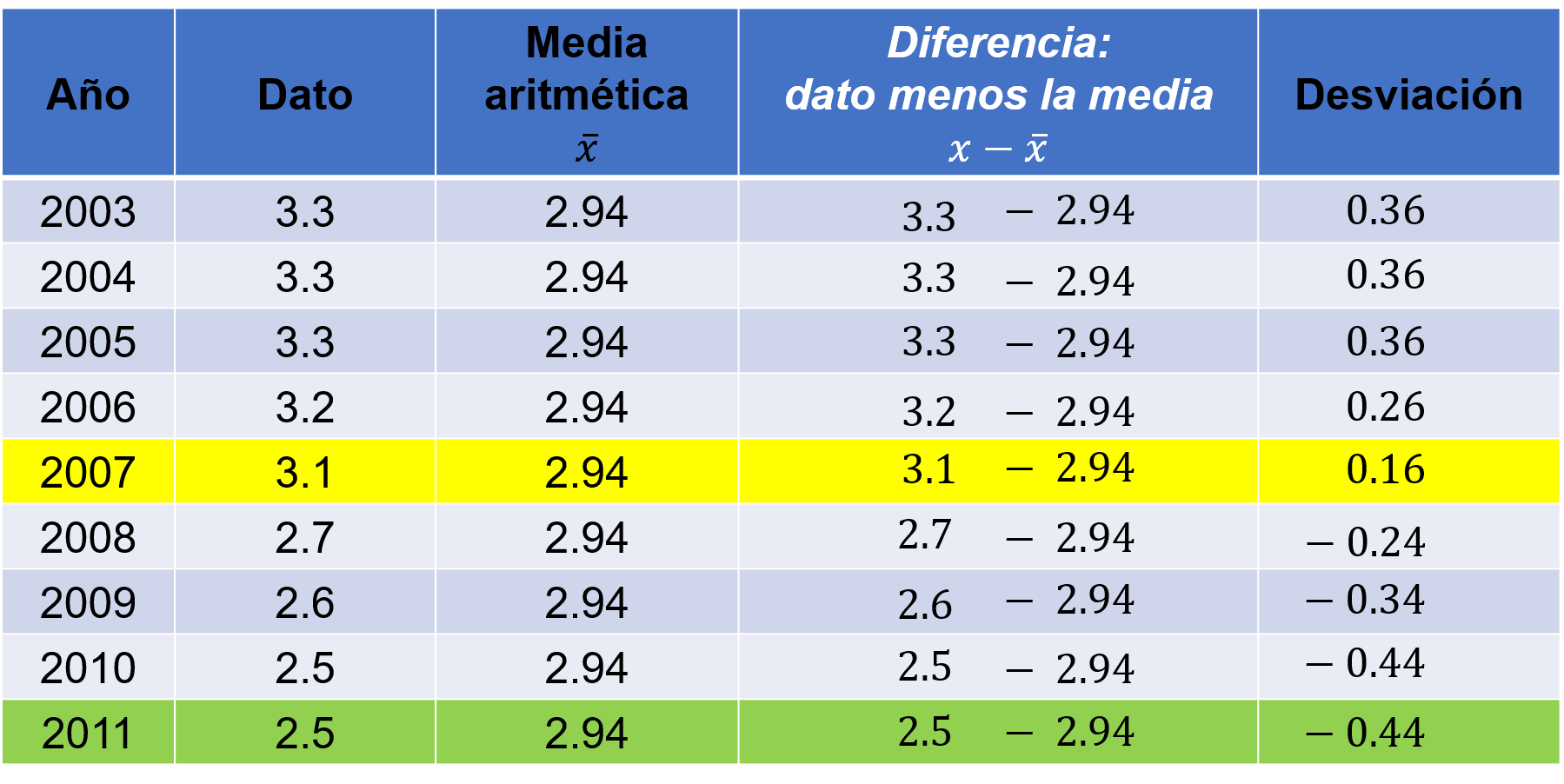
Para determinar la desviación realiza la resta de cada dato con el promedio y lo anotas en la quinta columna.
Con el análisis de los datos de la desviación en la tabla, se observa que el año con mayor desviación absoluta es el año 2011 y el 2007 es el año con menor desviación absoluta.
Ahora observa que, para determinar la desviación media, obtienes los valores absolutos de las desviaciones, en la cuarta columna, después obtienes la suma de los valores absolutos de las desviaciones y determinas su promedio, dividiendo esta suma entre el número de datos, que es 9, y entonces, encuentras la desviación media de los datos de la producción de petróleo del año 2003 al 2011, que fue de 0.33 millones de barriles al día.
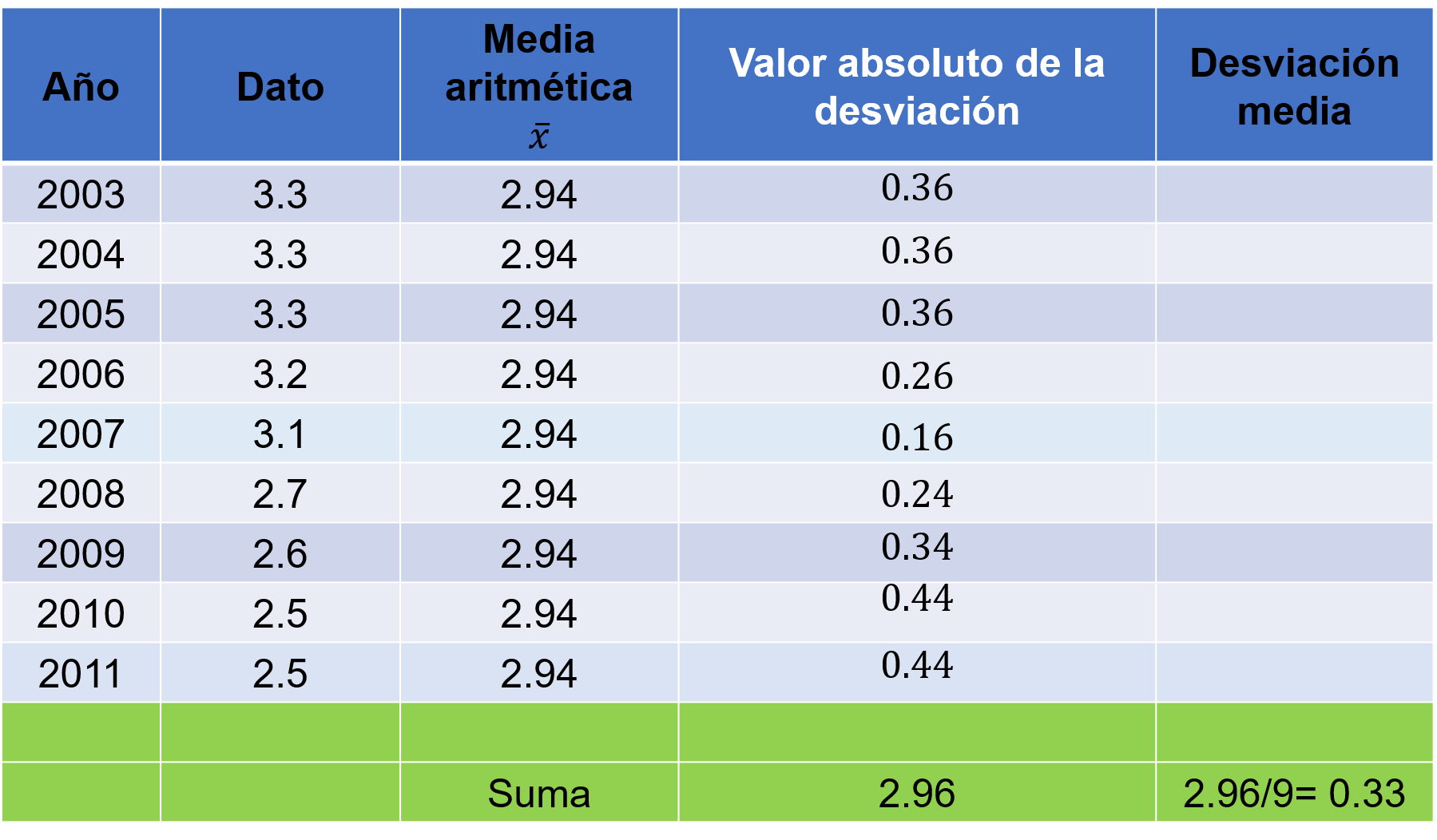
Lo que quiere decir que la mayoría de los datos se encuentran dentro de la desviación media.
El promedio es de 2.94 millones de barriles y la desviación media es de 0.33, entonces la mayoría de los datos están entre 2.94 – 0.33 y 2.94 + 0.33, esto es entre 2.61 y 2.67 millones de barriles.
Analiza otra situación.
Observa y analiza la siguiente gráfica para responder algunas preguntas.
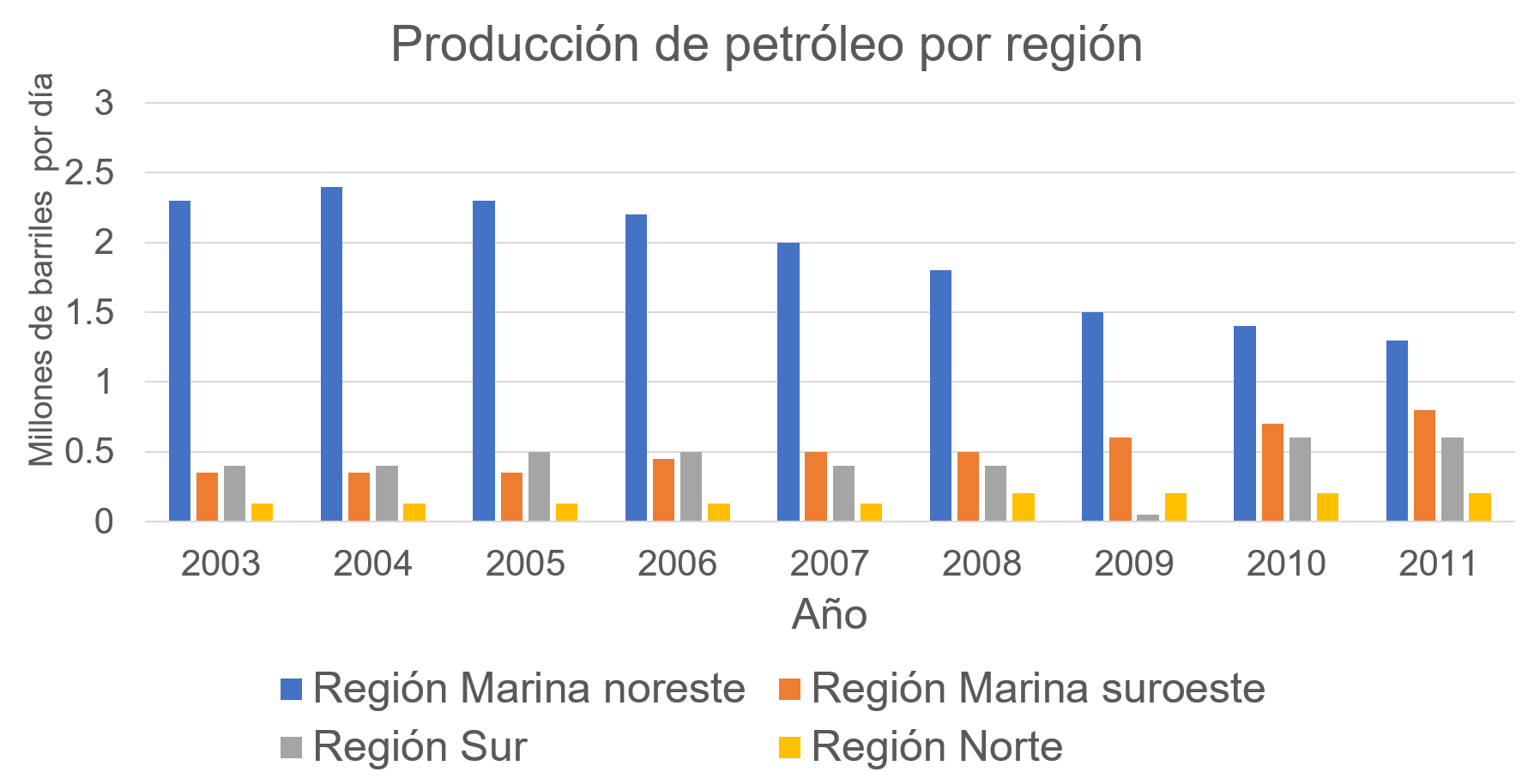
¿Qué región del país aporta mayor cantidad de petróleo?
¿Qué región del país produce menor cantidad de petróleo?
Observa que la región de país que genera mayor cantidad de petróleo es la Región Marina Noreste y la región que genera menor cantidad es la Región Norte.
Ahora, con base en los datos de la gráfica, obtén las medidas estadísticas de promedio, desviación y media y rango, de la Región Marina Noreste y la Región Norte.
Para la Región Marina Noreste la media es igual a la suma de 2.3 millones más, 2.4 millones más, 2.3 millones más, 2.2 millones, más 2 millones, 1.8 millones más 1.5 millones más, 1.4 millones más, 1.3 millones, todo entre 9, que es el total de datos.
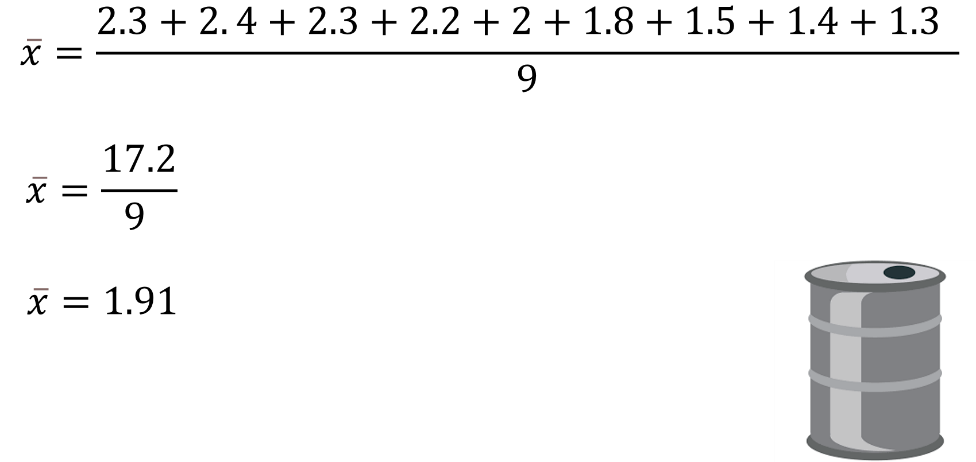
Igual a 0.38 más, 0.48, más 0.38, más 0.28, más 0.08, más 0.12, más 0.42, más 0.52, más 0.62, todo entre 9.
Igual a 17. 3 entre 9, por lo tanto, el promedio de los datos de producción de barriles petróleo por día es igual a 1.92 millones.
La desviación media es igual a la suma de la diferencia del valor absoluto de 2.3 menos 1.92, más el valor absoluto de 2.4 menos 1.92, más el valor absoluto 2. 3 menos 1.92, más el valor absoluto de 2.2 menos 1.92, más el valor absoluto de 2 menos 1.92, más el valor absoluto de 1.8 menos 1.92, más el valor absoluto de 1.5 menos 1.92, más el valor absoluto de 1. 4 menos 1. 92, más el valor absoluto de 1.3 menos 1.92, todo entre 9, que es el total de datos.

Igual a 0.38 más, 0.48, más 0.38, más 0.28, más 0.08, más 0.12, más 0.42, más 0.52, más 0.62, todo entre 9.
Igual a 3.2 entre 9, igual 0.35
Por lo tanto, la desviación media es igual a 0.35 millones de barriles de petróleo.
El rango es igual a la diferencia de 2.4 millones menos 1.3 millones, es igual a 1.1 millones.
Para la Región Norte, la media es igual a la suma de 0.13 millones más, 0.13 millones más, 0.13 millones más, 0.13 millones, más 0.13 millones, 0. 2 millones más 0. 2 millones más, 0. 2 millones más, 0. 2 millones, todo entre 9, que es el total de datos.

Igual a 1.45 entre 9, por lo tanto, el promedio de los datos de producción de barriles petróleo por día es igual a 0.16 millones.
La desviación media es igual a la suma de la diferencia del valor absoluto de 0.13 menos 0.16, más el valor absoluto de 0.13 menos 0.16, más el valor absoluto 0.13 menos 0.16, más el valor absoluto de 0.13 menos 0.16, más el valor absoluto de 0.13 menos 0.16, más el valor absoluto de 0.2 menos 0.16, más el valor absoluto de 0.2 menos 0.16, más el valor absoluto de 0.2 menos 0.16, más el valor absoluto de 0.2 menos 0.16, todo entre 9 que es el total de datos.

Igual a 0.03 más, 0.03, más 0.03, más 0.03, más 0.03, más 0.04, más 0.04, más 0.04, más 0.04, todo entre 9.
Igual a 0.31 entre 9, igual 0.034
Por lo tanto, la desviación media es igual a 0.034 millones de barriles de petróleo.
El rango es igual a la diferencia de 0.2 millones menos 0.13 millones, es igual a 0.07 millones.
Las medidas de dispersión o de variabilidad expresan cómo se distribuyen los datos en torno a alguna de las medidas de tendencia central, son un complemento a estas últimas para describir más fielmente un conjunto de datos.
El reto de hoy:
En la historia de las matemáticas existe un matemático, historiador y pensador británico, quien estableció la disciplina de la estadística matemática; también fue que el fundador de la bioestadística, que es la aplicación de la estadística a la biología, él es: Karl Pearson.
El reto es investigar más sobre este matemático.
Busca y resuelve en tu libro de texto, los problemas relacionados con el tema y fortalecer tu proceso de aprendizaje a distancia.
¡Buen trabajo!
Gracias por tu esfuerzo.