Teselados III
Teselados III
Aprendizaje esperado: deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.
Énfasis: analizar las características de los teselados para su construcción I.
¿Qué vamos a aprender?
En esta sesión analizarás las características de los teselados para su construcción. La construcción la harás con ayuda de una aplicación de geometría dinámica: GeoGebra.
También, analizarás las propiedades de los polígonos regulares e irregulares para construir teselados o mosaicos que cubren el plano sin dejar espacio entre
sus piezas.
¿Qué hacemos?
Los teselados son algo que está presente en la vida cotidiana, aunque algunas veces no nos damos cuenta de ello.
La palabra teselados proviene de “tessellae”. Así era como llamaban los romanos a las construcciones y pavimentos de su ciudad. En las antiguas civilizaciones utilizaban teselados para las construcciones de sus casas y templos, esto ya se hacía cerca del año 4,000 antes de nuestra era.

Un teselado es un mosaico formado por la repetición de una figura geométrica que puede ser regular o irregular, y que cubre dentro de una superficie plana sin dejar espacios o sobreponerse.
Las características principales de los teselados son:
- Se hacen partiendo del uso de polígonos regulares o irregulares.
- No pueden tener espacios entre ellas o estar sobrepuestas.
- Las figuras se unen en un vértice común, donde se forma un ángulo de 360 grados.
- Consta de partes iguales que son divisibles por la mitad desde diferentes ángulos, para formar partes simétricas.
Ahora conocerás los tipos de teselados.
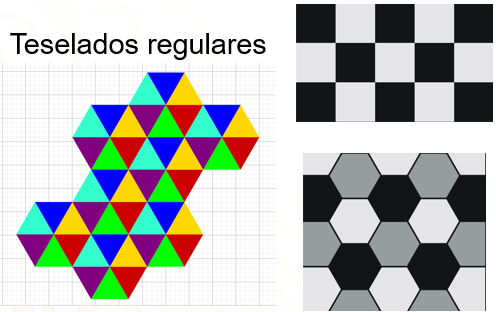
Teselados regulares
Se logran mediante la repetición de polígonos regulares. No cualquier polígono regular puede ser teselar en plano. Sólo existen tres teselaciones regulares.
- Triangulares
- Cuadrangulares
- Hexagonales
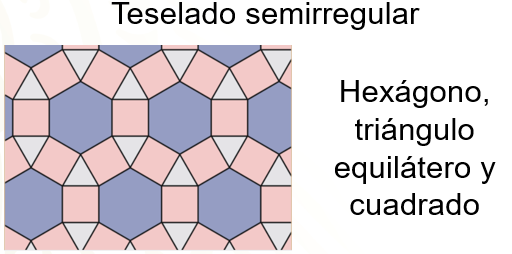
Teselados semirregulares
Están hechos con la combinación de dos o más polígonos regulares. En este tipo de teselados, el patrón utilizado debe de ser el mismo en cada vértice.
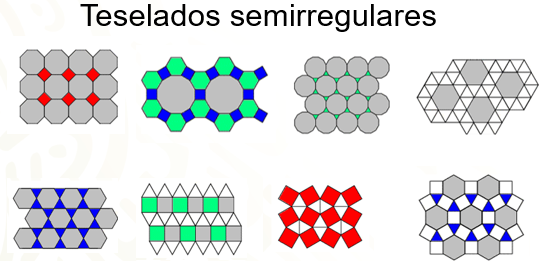
Existen 8 teselaciones semirregulares, que están formados por las siguientes figuras:
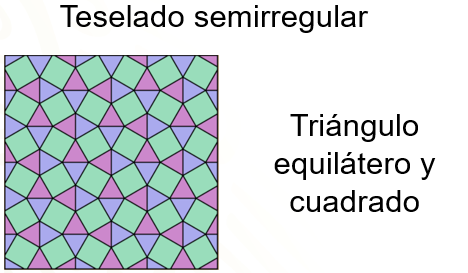
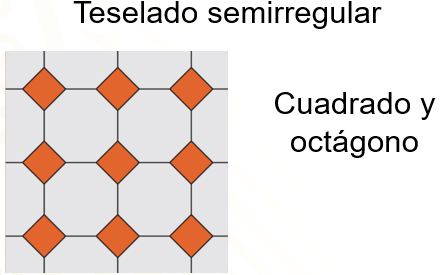
Cuadrados y octágonos; cuadrados, dodecágonos y hexágonos; triángulos equiláteros y dodecágonos; 2 compuestos por triángulos equiláteros y hexágonos; 2 formados por triángulos equiláteros y cuadrados; y uno más integrado por triángulos equiláteros, cuadrados y hexágonos. Observa algunos ejemplos de teselados semirregulares.
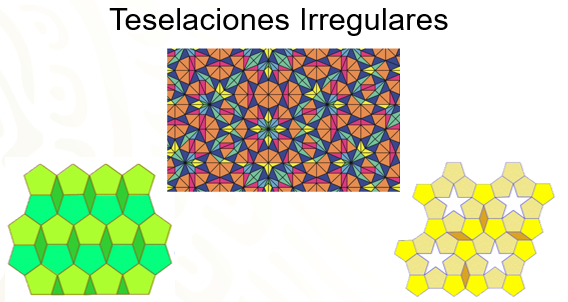
Teselaciones Irregulares.
Los teselados irregulares están construidos a partir de polígonos regulares e irregulares que, al igual que todas las teselaciones, cubren toda la superficie sin sobreponerse ni dejar espacios vacíos. La distribución de los polígonos en los distintos vértices es cíclica; pueden darse 3, 4, 5 y más distribuciones que harán que la periodicidad sea más espaciada, requiriendo dibujar una gran porción de la tesela para poder ver un ciclo completo. Para ver tal efecto, observa dos ejemplos de la distribución del pentágono:
Teselaciones en la vida cotidiana.
Las teselaciones se encuentran en todo el mundo natural.
¿Dónde podemos encontrar teselaciones naturales?
Ellos se encuentran, por ejemplo, en los prismas basálticos, en la piel de las serpientes, en el caparazón de una tortuga, así como en el panal que construyen las abejas.

¿En dónde más puedes encontrar ejemplos de teselados en el mundo natural?
Registra tus respuestas en el cuaderno.
A continuación, llevarás a cabo algunas construcciones de teselaciones con la aplicación de la geometría dinámica GeoGebra. Antes de comenzar, debes configurar ciertas condiciones en la hoja de GeoGebra.
Cuando se abre la aplicación de GeoGebra Clásico se muestra una hoja como la siguiente:
Lo primero que harás es cerrar una ventana que se encuentra en la parte superior derecha de esa hoja.
La configuración que te conviene para la construcción de las teselaciones es tener una vista gráfica que tenga la cuadrícula. Presiona el botón de ocultar los ejes “x” y “y”, ya que necesitas que la vista gráfica ordene por tipo de objeto.
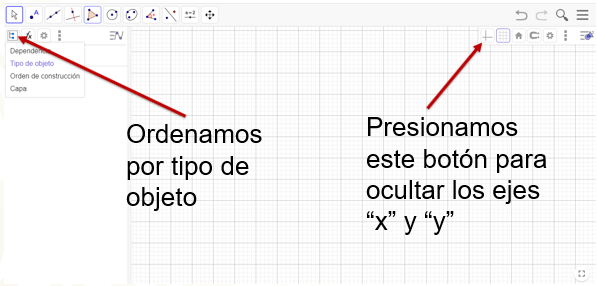
A continuación, presiona el botón de menú que se encuentra en la parte superior derecha, y selecciona la opción Propiedades.
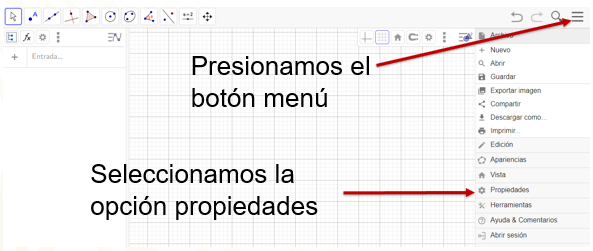
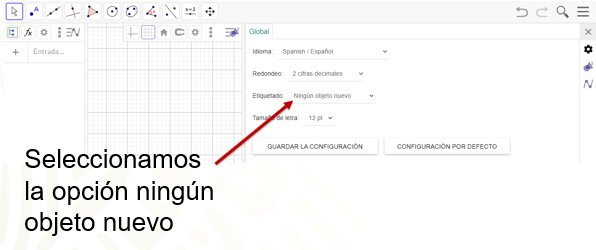
En la ventana que se despliega, selecciona la opción Ningún
objeto nuevo. Guarda la configuración, si quieres seguir construyendo teselaciones.
Llevarás a cabo tus primeras construcciones en GeoGebra.
En este reto 1 construirás tu primera teselación regular a partir de un triángulo equilátero. Debes tener presente que cada ángulo interior de un triángulo equilátero mide 60 grados. Entonces, si se une un vértice de cada uno de 6 triángulos equiláteros en un mismo punto, de forma que cada lado de un triángulo coincida con el del otro, la suma de los 6 ángulos interiores que se juntan es de 360 grados.
Esta es una de las características de los teselados.
- Video: teselados 1.080321
https://youtu.be/6pOVrvGHP8Y
(del min. 3.20 al 6.23) )
Una manera de comprobar que un triángulo equilátero llena toda la superficie de un plano en GeoGebra es la siguiente.
Selecciona la opción Polígono regular que se encuentra en la barra de herramientas. Traza un polígono regular con una longitud de cuatros cuadros. Escribe el número 3, que es el número de lados del polígono.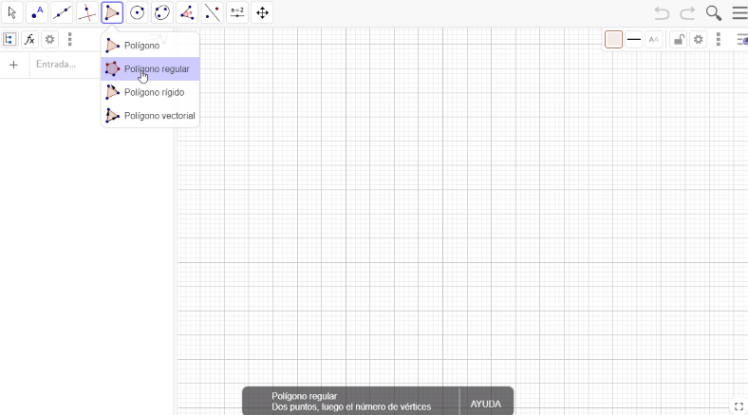
Ubícate dentro de la superficie del triángulo, presiona el botón derecho del mouse y selecciona la opción Propiedades. Posteriormente, ingresa a la pestaña con el nombre de Color, en este caso selecciona el color verde con una opacidad del 100 y en la pestaña con el nombre de Estilo, el grosor del trazo lo dejarás en cero.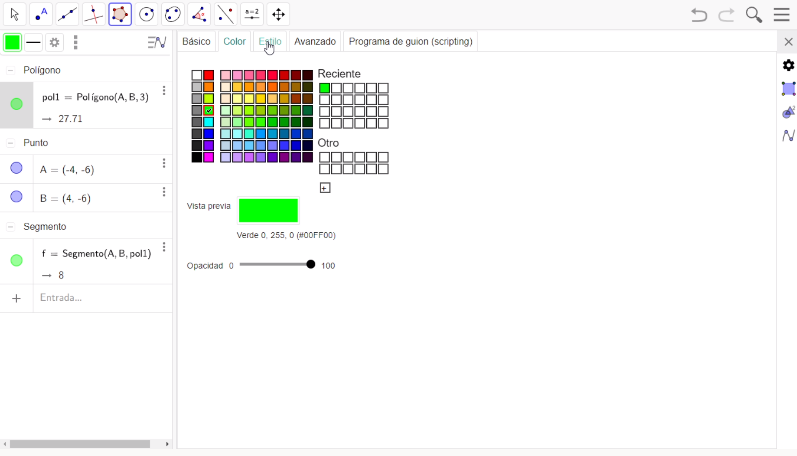
En la barra de herramientas, selecciona la opción Rotación, para ubicar un nuevo triángulo del lado derecho al original. El punto de rotación será el vértice superior del triángulo. Lleva a cabo una rotación de 60° con un sentido antihorario.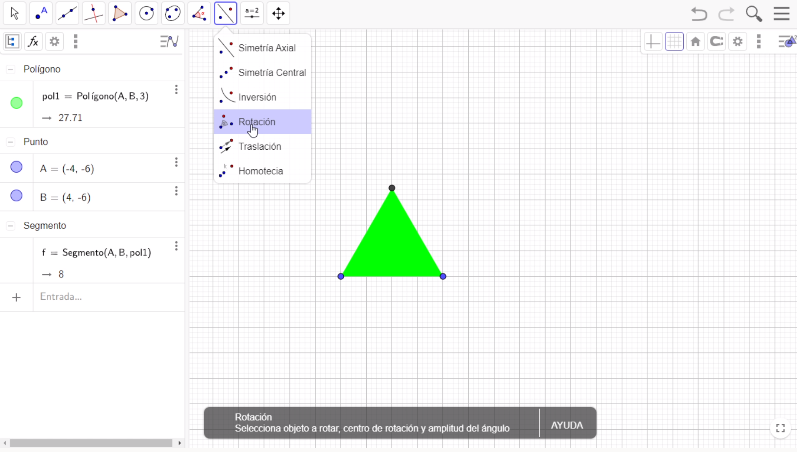
Ubícate dentro de la superficie del nuevo triángulo, presiona el botón del lado derecho del mouse. En el menú que así aparece, selecciona la opción Propiedades para entrar a la pestaña con el nombre de Color y escoger el color rojo.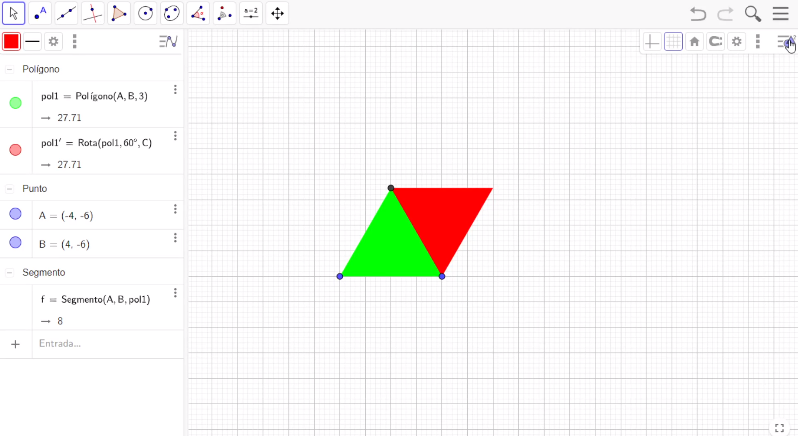
Este proceso de rotación y color del triángulo lo llevarás a cabo cuatro veces más, con los siguientes colores, azul, morado, amarillo y naranja.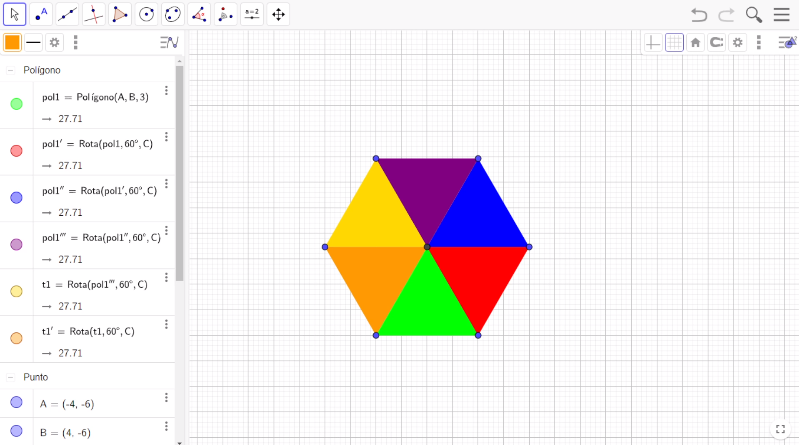
De esta manera, has unido 6 triángulos equiláteros del mismo tamaño alrededor de un punto, sin sobreponerse ni dejar huecos, es decir, has comenzado a teselar el plano.
Ahora, continua con esta teselación trasladando toda la configuración anterior. Una forma de trasladar estos 6 triángulos equiláteros es seleccionar en la barra de herramientas la opción Recta y escoger la opción Vector. Luego, traza un vector del vértice inferior izquierdo del triángulo amarillo al vértice superior derecho del triángulo morado y otro vector del vértice inferior izquierdo del triángulo amarillo al vértice inferior derecho del triángulo verde.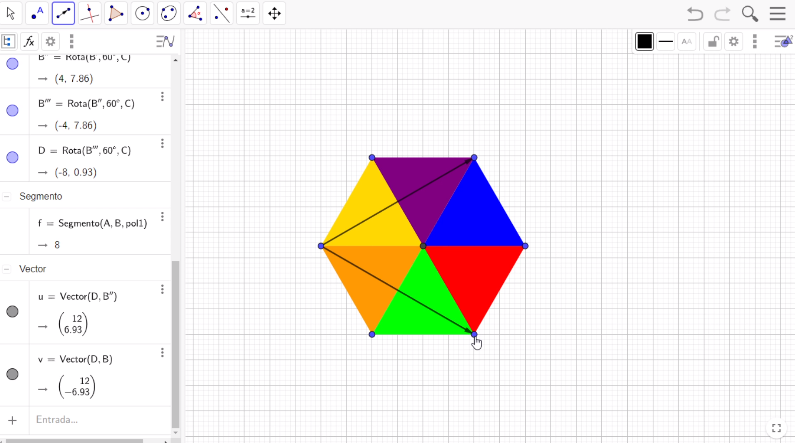
En la barra de herramientas, abre la ventana de Simetría Axial y ahí elige la opción Traslación. Luego, presiona el botón izquierdo del mouse, y construye un cuadrilátero encerrando los 6 triángulos equiláteros. Después, selecciona y presiona el vector con el sentido hacia arriba.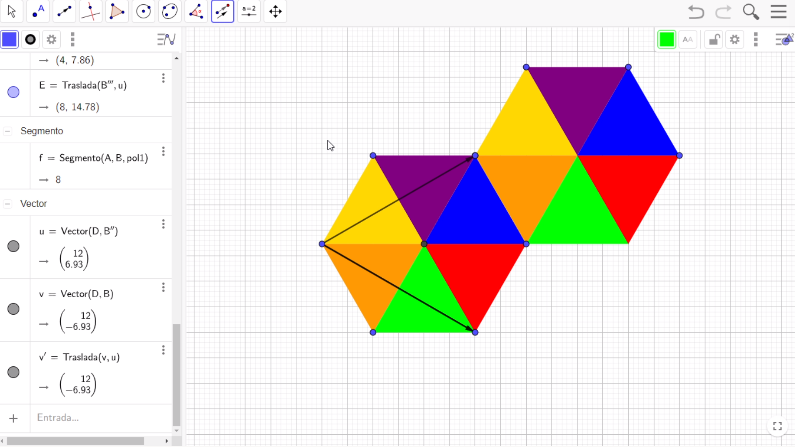
Llevarás a cabo este proceso 3 veces, encerrando todos los triángulos con un cuadrilátero y presionando el vector con sentido hacia arriba. De la misma forma lo harás con el vector del sentido hacía abajo.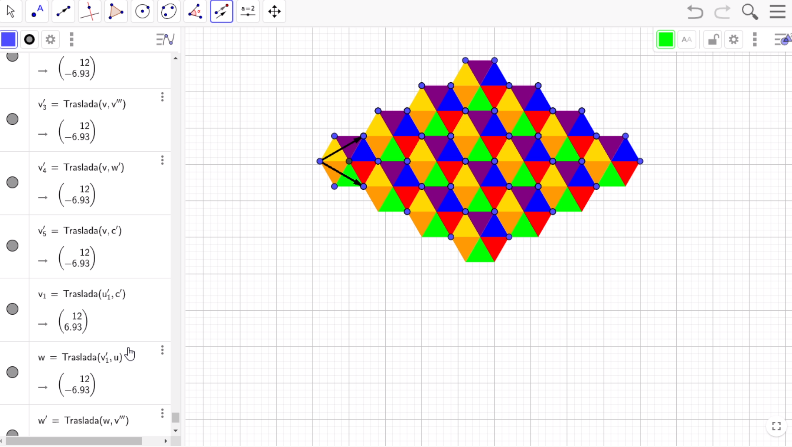
Una forma de quitar los puntos y los vectores en el teselado, es mover la barra de desplazamiento vertical hasta arriba en el espacio de elementos de entrada, ubícate en el botón izquierdo de polígono y presiónalo. Después, selecciona la palabra Punto y con el botón derecho del mouse toca la parte sombreada y presiona la opción Objeto visible. Haz el mismo proceso con los vectores. Por último, selecciona el vértice superior del primer triángulo con el botón derecho del mouse y presiona la opción Objeto visible.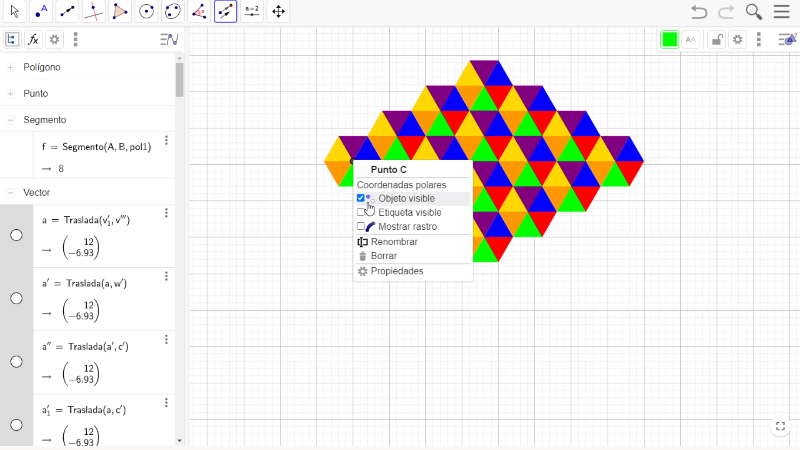
Realiza una segunda construcción. - Video: teselados 2.080321
https://youtu.be/6pOVrvGHP8Y
(del min. 8.23 al 13.22)
Construirás esta segunda teselación regular a partir de un cuadrado. Cada ángulo interior de un cuadrado mide 90 grados. Se debe unir un vértice de cada uno de 4 cuadrados en un mismo punto, para que juntos, formen un ángulo de 360 grados.
Recuerda que ésta es una de las características de los teselados.
Una forma de comprobar que un cuadrado llena toda la superficie de un plano en GeoGebra es la siguiente:
Selecciona la opción Polígono regular en la barra de herramientas. Traza un polígono regular de cuatro lados con una longitud de cuatros cuadros.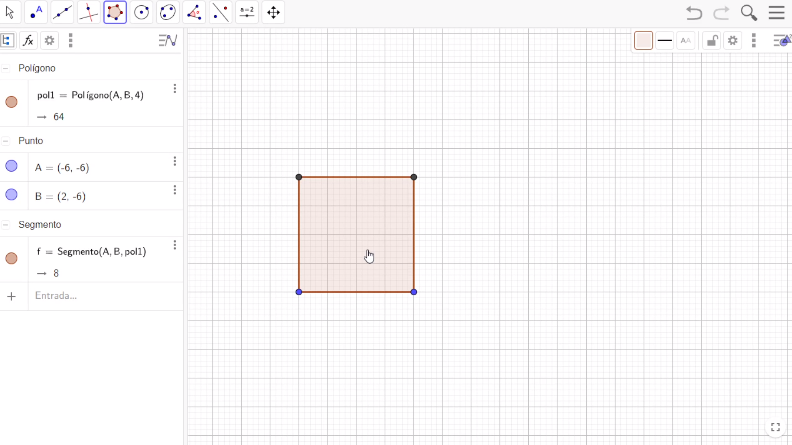
Ubícate dentro de la superficie del cuadrado, presiona el botón derecho del mouse y selecciona la opción Propiedades. Posteriormente, entra a la pestaña con el nombre de Color; en este caso selecciona el color verde con una opacidad del 100 y en la pestaña con el nombre de Estilo, el grosor del trazo lo dejarás en cero.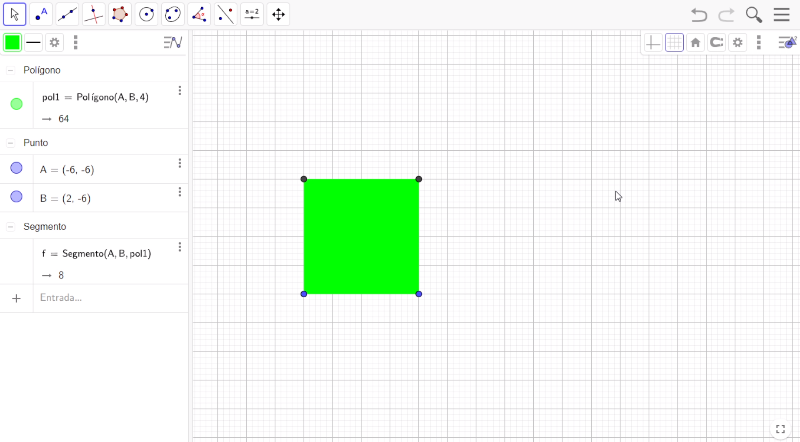
A continuación, selecciona la herramienta de Rotación; encierra en un cuadrilátero el primer cuadrado, para ubicar un nuevo cuadrado en la parte superior al original. El punto de rotación será el vértice superior del lado izquierdo y llevarás a cabo una rotación de 90 grados con un sentido antihorario.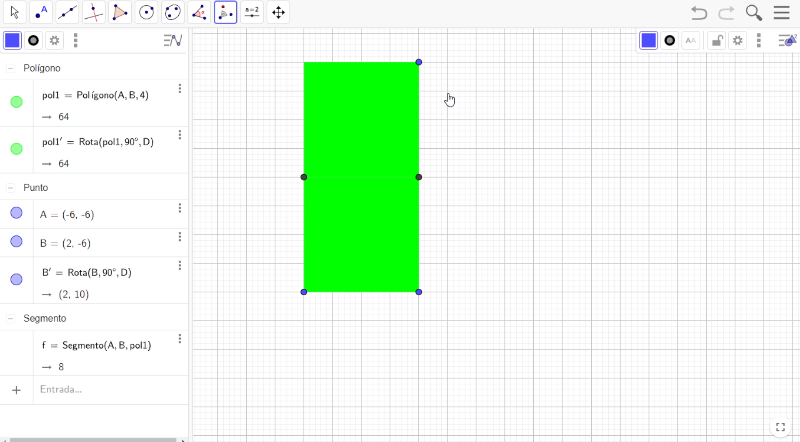
Te diste cuenta de que el vértice que se encontraba en la parte inferior derecha no se rotó. Ahora selecciona el segundo cuadrado y rótalo 90 grados en un sentido antihorario con respecto al vértice superior izquierdo del cuadrado original.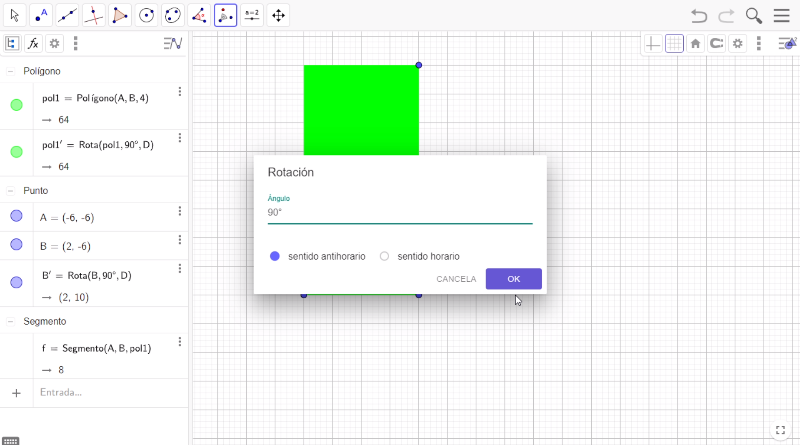
Nuevamente selecciona la herramienta de Rotación, encierra en un cuadrilátero el segundo cuadrado. Para ubicar un nuevo cuadrado en la parte superior del lado izquierdo con respecto al segundo, nuestro punto de rotación será el vértice superior del lado izquierdo del cuadrado original. Lleva a cabo una rotación de 90 grados con un sentido antihorario.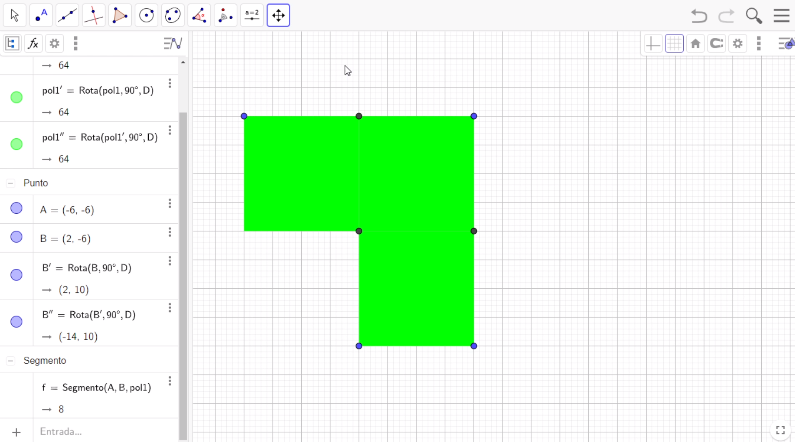
Por último, encierra en un cuadrilátero el tercer cuadrado, para ubicar un nuevo cuadrado en la parte inferior con respecto al tercer cuadrado. El punto de rotación será el vértice superior del lado izquierdo del cuadrado original. Lleva a cabo una rotación de 90 grados con un sentido antihorario.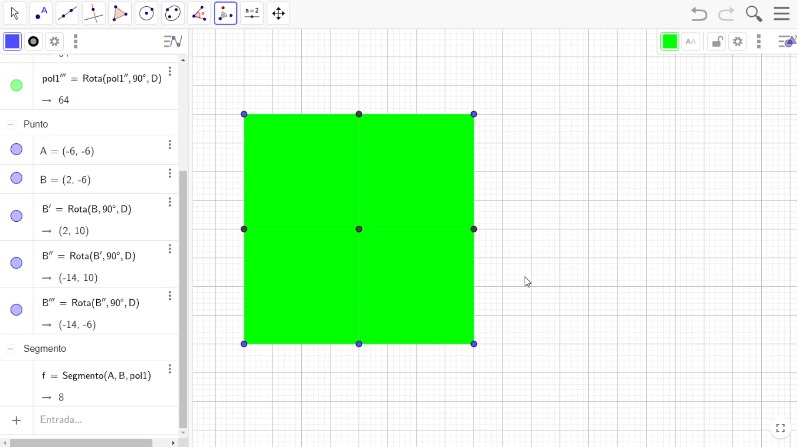
Ahora, ubícate dentro de la superficie del segundo cuadrado. Presiona el botón del lado derecho del mouse y selecciona la opción “Propiedades” para entrar a la pestaña con el nombre de Color y escoger el color rojo. Posteriormente, ubícate dentro del tercer cuadrado, presiona el botón del lado derecho del mouse, selecciona la opción “Propiedades” para entrar a la pestaña con el nombre de Color y escoger el color amarillo y, finalmente, haz lo mismo con el cuarto cuadrado escogiendo el color azul.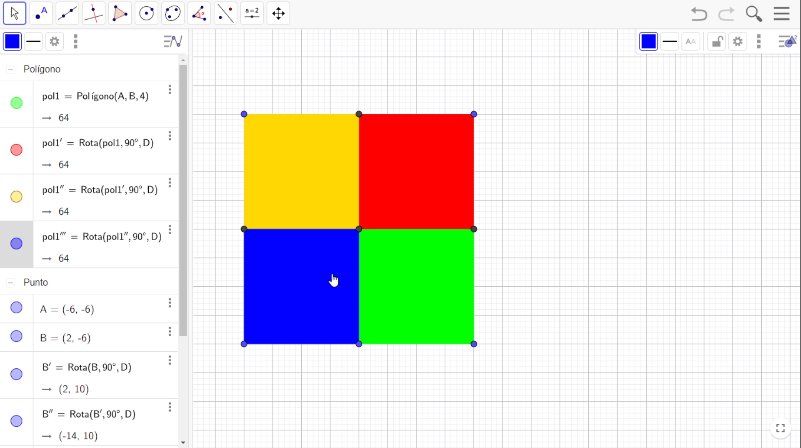
Elimina los puntos medios y el central de la figura.
Una forma de trasladar estos 4 cuadrados es seleccionar la opción Rectas en la barra de herramientas y escoge la opción Vector. Traza un vector del vértice inferior izquierdo del cuadrado azul al vértice inferior derecho del cuadrado verde y otro vector del vértice inferior izquierdo del cuadrado azul al vértice superior izquierdo del cuadrado amarillo. Ahora, elige la opción “Traslación” en la barra de herramientas y presiona el botón izquierdo del mouse. Construiste un cuadrilátero encerrando los 4 cuadrados, después selecciona y presiona el vector con el sentido hacia la derecha. Lleva a cabo este proceso 2 veces, encerrando todos los cuadrados con un cuadrilátero y presionando el vector con sentido hacia derecha, de la misma forma lo harás con el vector con el sentido hacia arriba.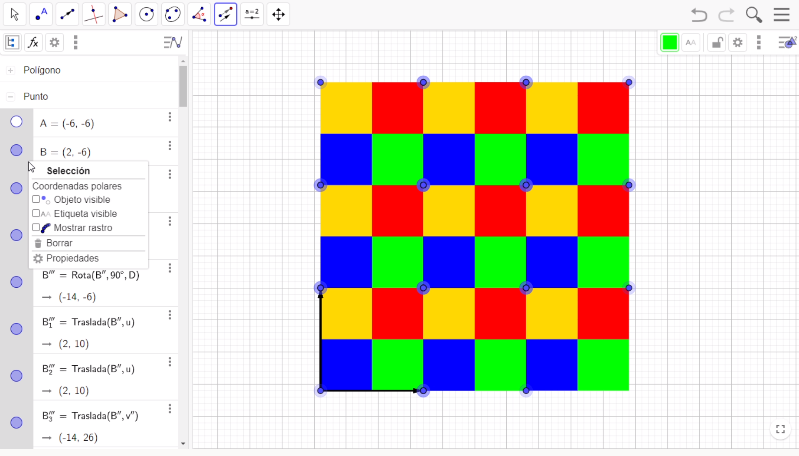
Una forma de quitar los puntos y los vectores en el teselado, es mover la barra de desplazamiento vertical hasta arriba en el espacio de elementos de entrada, ubícate en el botón izquierdo de Polígono y presiónalo; después, selecciona “Punto” y con el botón derecho del mouse toca la parte sombreada y presiona la opción “objeto Visible”, haz el mismo proceso con los vectores. Por último, selecciona el vértice superior del primer cuadrado con el botón derecho del mouse y presiona la opción “Objeto visible”. Así, has construido un teselado regular con cuadrados.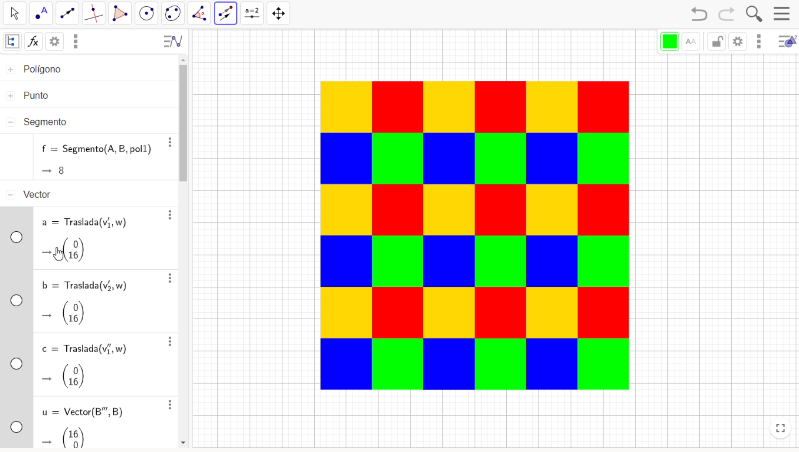
Varios artistas son conocidos por sus obras que contienen teselados, cada una de ellas se adaptó a su estilo, tanto artístico, como al uso de materiales. Uno de ellos fue Maurits Cornelis Escher, artista holandés, nacido en 1898. Conocido por sus grabados, teselados y figuras llamadas “imposibles”.
Continua con otra actividad para construir teselados.
Emmanuel debe elaborar cenefas para decorar las paredes de su aula. Él encontró en internet los mosaicos nazaríes que llamaron su atención y eligió uno que se elabora a partir de la figura de un avión, como el que se muestra en la imagen.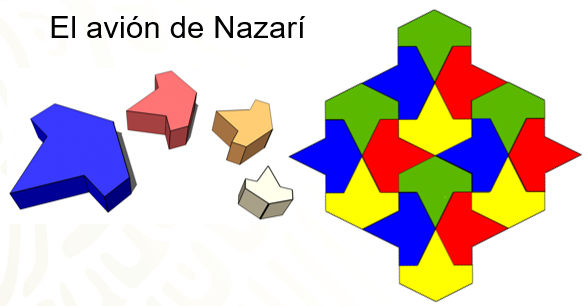
¿Qué transformaciones deberá aplicar Emmanuel al avión de Nazarí para elaborar la cenefa que colocará en las paredes de su aula? - Video: Avión de Nazarí
(del min. 13.34 al 23.52)
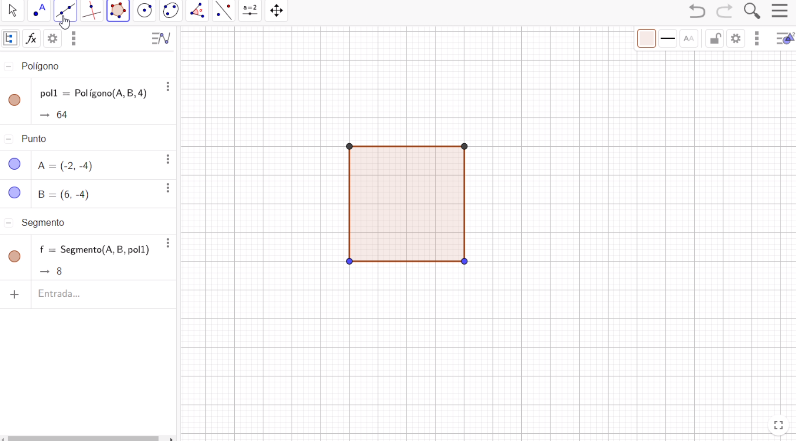
Traza un polígono regular de cuatro lados con una longitud de cuatros cuadros, escribimos el número 4.
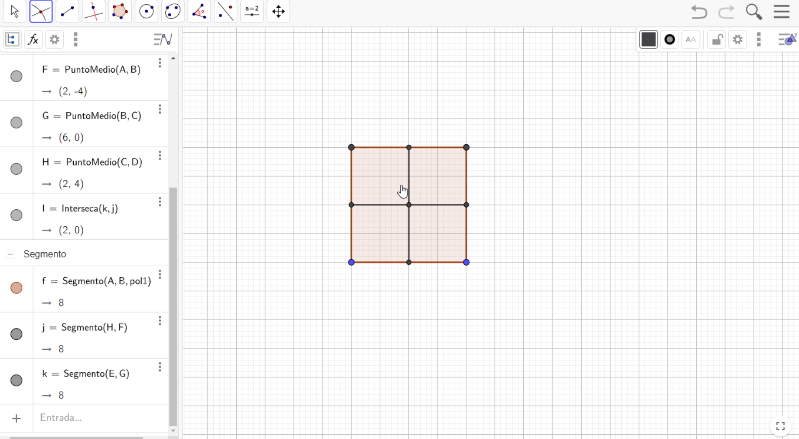
El siguiente paso es trazar dos segmentos perpendiculares. Los harás usando el punto medio de cada lado, así que, en la barra de herramientas elige la opción Punto medio y ve marcando los vértices del cuadrado para que se vayan ubicando los puntos medios de sus lados. Puedes empezar con cualquier vértice. Una vez que tienes los 4 puntos medios, vas a trazar dos segmentos; así que en la barra de herramientas selecciona la opción Segmento y une los puntos medios con dos rectas perpendiculares. Ahora, el siguiente paso es ubicar la intersección de estos dos segmentos; para ello, en la barra de herramientas, busca la opción Intersección y selecciona las dos rectas centrales. De esta manera, aparece la intersección en la figura.
Ubica el punto medio en la base inferior del cuadrado superior izquierdo, ve a la barra de herramientas y selecciona la opción Medio o Centro y localiza el punto medio.
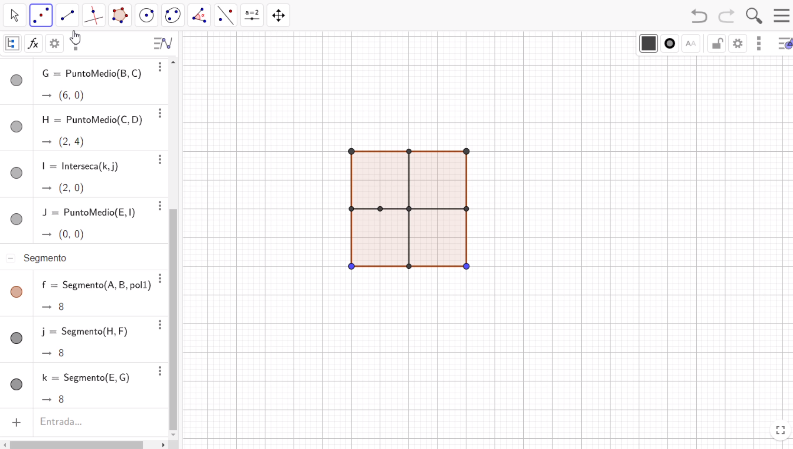
Une con un segmento el nuevo punto medio con el punto medio del lado superior del cuadrado original.
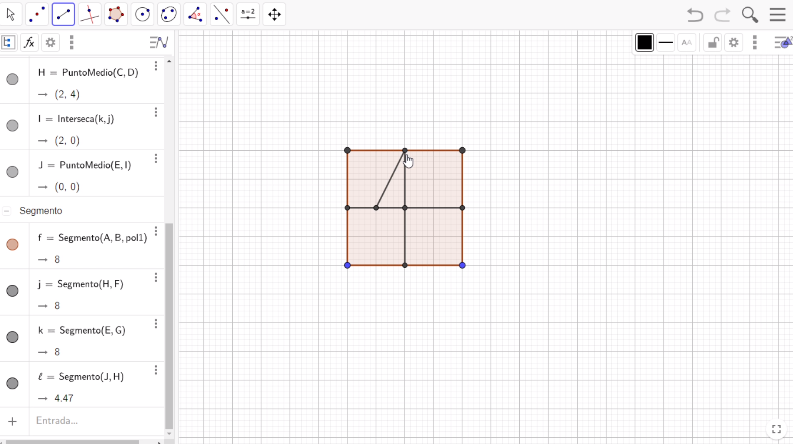
El siguiente paso es hacer una rotación, es decir, un giro del segmento que pueda pasar por el punto medio del lado izquierdo del cuadrado original y el punto medio de la base del cuadrado original. Selecciona la herramienta de “Rotación”; se rota alrededor del punto medio del lado izquierdo del cuadrado original, con un giro de 90
grados en sentido horario.
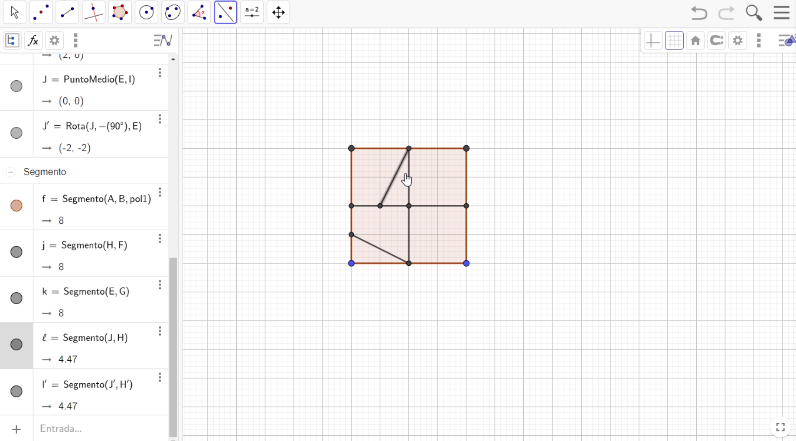
Ahora, utiliza la simetría axial. Ve a la barra de herramientas y selecciona “Simetría axial” para reflejar los dos segmentos que se encuentran en forma diagonal. Presiona el botón izquierdo del mouse tocando la diagonal y posteriormente el eje de simetría donde se reflejará ésta. Haz esto con las dos diagonales.
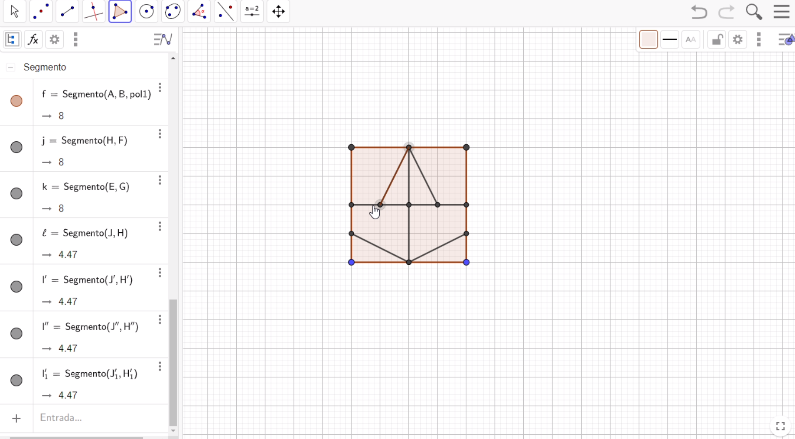
Ya tienes marcada la estructura del Avión. Ahora, lo tienes que dibujar para tenerlo como un objeto independiente. Eso lo harás con la herramienta Polígono, procede a seleccionar algunos de los puntos que conforman la estructura del avión y que lo determinan completamente. Empezarás con el punto medio del lado superior del cuadrado original. Aquí puedes elegir el color, así que le vas a dar otro color para poder diferenciar la estructura del avión de Nazarí.
Ubícate dentro de la superficie del avión; presiona el botón derecho del mouse y selecciona la opción Propiedades. Posteriormente, entra a la pestaña con el nombre de Color y selecciona el color Amarillo con una opacidad del 100 y en la pestaña con el nombre de estilo, el grosor del trazo déjalo en cero.
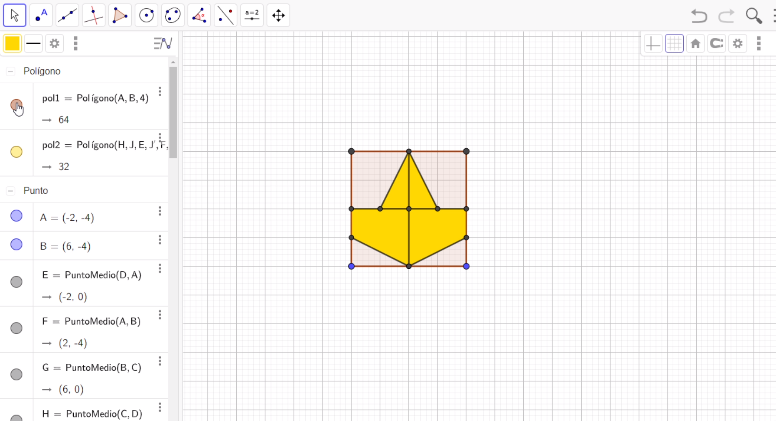
El siguiente paso es dejar de forma más sencilla la estructura del avión, para ello ocultarás el cuadrado, los segmentos y los puntos que no necesitas.
Oculta el cuadrado de la siguiente manera: pasa a la Vista algebraica y selecciona “Polígonos”; después, presiona el botón del lado izquierdo del polígono 1, desapareciendo así el cuadrado de la vista gráfica. Después presiona los botones del lado izquierdo de los puntos A y B.
Posteriormente, quita los segmentos de la vista gráfica. Para lograrlo, basta con presionar una vez el botón izquierdo sobre los siguientes segmentos J, K, L, L prima, L biprima, L1 prima.
Luego, regresa a la vista algebraica para quitar el punto I de la vista gráfica presionando el botón que se encuentra del lado izquierdo del punto I. Los puntos C y D los quitarás de forma manual; selecciona con el botón derecho del mouse el vértice superior derecho y presiona con el botón izquierdo Objeto visible; haz lo mismo con el vértice superior izquierdo.
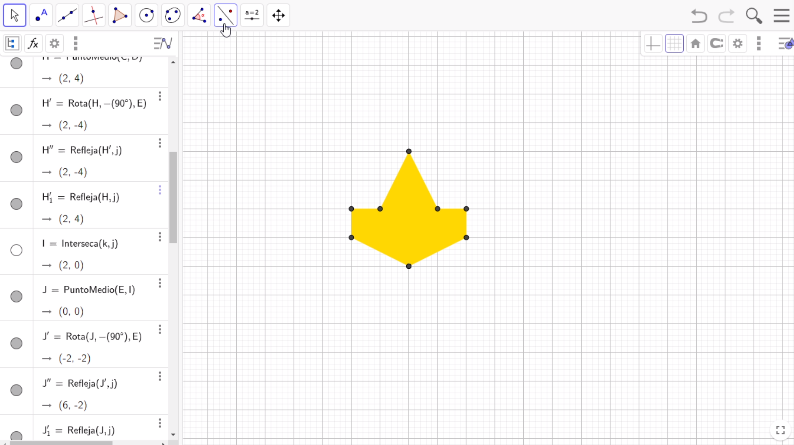
El siguiente paso es rotar el avión respecto al vértice superior de su ala derecha. Selecciona “Rotación” en la barra de herramientas y encierra en un cuadrilátero todo el avión. Luego, selecciona el vértice mencionado y rótalo 90 grados en el sentido horario.
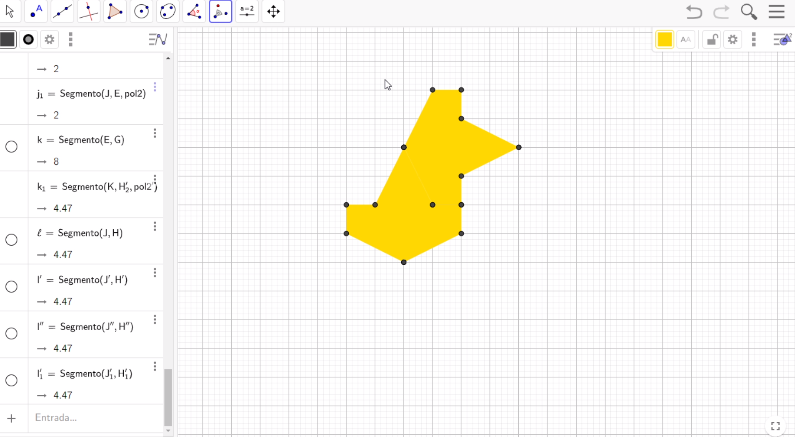
Este procedimiento lo repetirás otras dos veces más para tener cuatro aviones juntos, recordando que las rotaciones serán de 90 grados en sentido horario.
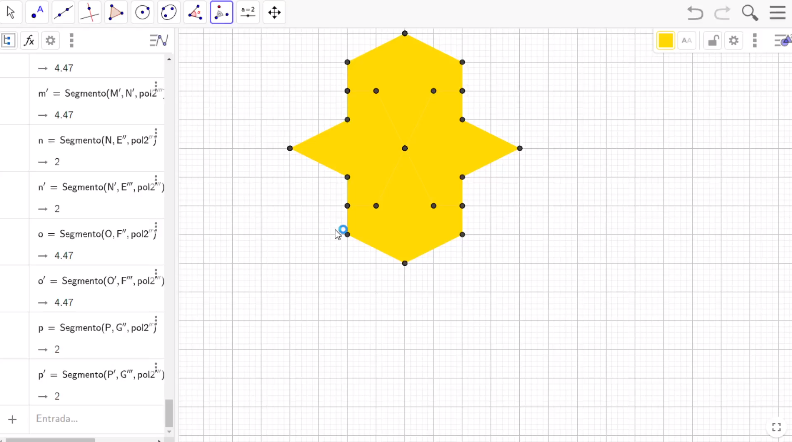
Una vez que terminaste con los cuatro aviones, cambia el color para apreciar de mejor manera el progreso del teselado.
Una manera de elegir los colores es ubicarte dentro de la superficie del segundo avión, presiona el botón del lado derecho del mouse, selecciona la opción “Propiedades” con el botón izquierdo del mouse, y accede a la pestaña Color. En este caso escoge el color rojo. Lleva este proceso dos veces más escogiendo los colores verde y azul.
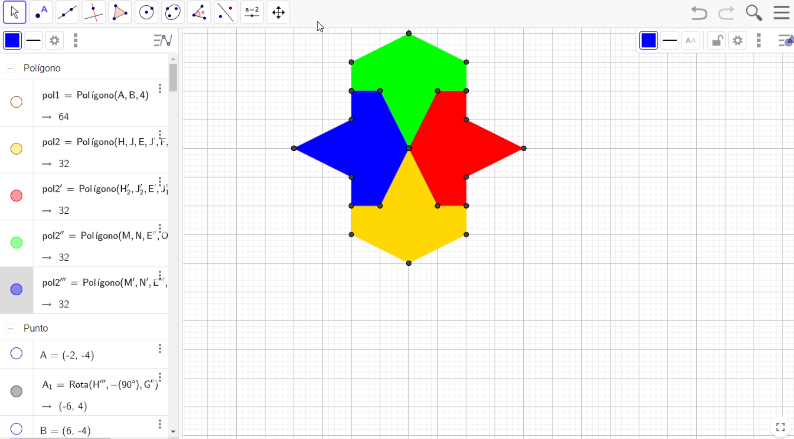
Ya tienes construido el patrón, lo que podemos llamar figura mínima para llenar el plano. Ahora, selecciona “Desplaza vista gráfica” en la barra de herramientas para acercar o alejar la figura. En este caso, lo alejarás de tal forma que puedas trasladarlo hacia arriba.
Vas a hacer la traslación de la figura mínima. Para ello, utilizarás el método del vector. Selecciona Vector en la barra de herramientas; posteriormente, ubicate en el vértice izquierdo del avión azul y proyecta el vector hasta el vértice superior del avión verde. Haz lo mismo, pero hacia abajo; ubícate en el vértice izquierdo del avión azul y proyecta el vector hasta el vértice inferior del avión amarillo. Luego, proyecta un tercer vector horizontal desde el vértice izquierdo del avión verde hasta el vértice derecho del avión rojo. Ahora, selecciona la opción traslación en la barra de herramientas, para, posteriormente, encerrar toda la figura inicial y presionar con el botón izquierdo del mouse el vector horizontal.
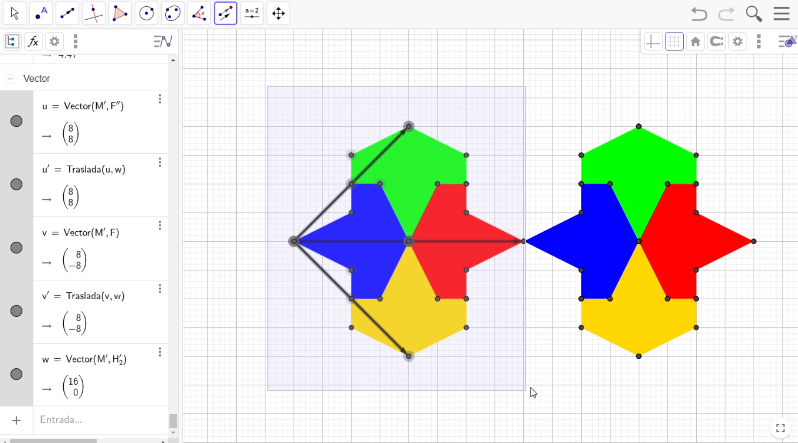
Haz este proceso dos veces más con los dos vectores restantes, recordando que debes encerrar la figura mínima para realizar las traslaciones.
Para finalizar, quita los puntos y los vectores. Para ello, ve a la parte superior de la vista algebraica, presiona el botón “Polígono”; después, presiona con el botón izquierdo del mouse donde está escrita la palabra “Punto”. ¿Te fijaste que todos los puntos se sombrearon de gris? Bien, ubicate en ese sombreado y con el botón derecho del mouse selecciona “Objeto visible” dos veces. Así, no tienes ningún punto en la vista gráfica. Presiona el botón de menos en Punto y en Segmento para cerrar todos los objetos; después, selecciona Vector con el botón izquierdo del mouse, ubícate en la parte sombreada y con el botón derecho del mouse selecciona “Objeto visible”. Hemos quitado los vectores de la vista gráfica.
Por último, selecciona “Desplaza vista gráfica” en la barra de herramientas para acercar el teselado.
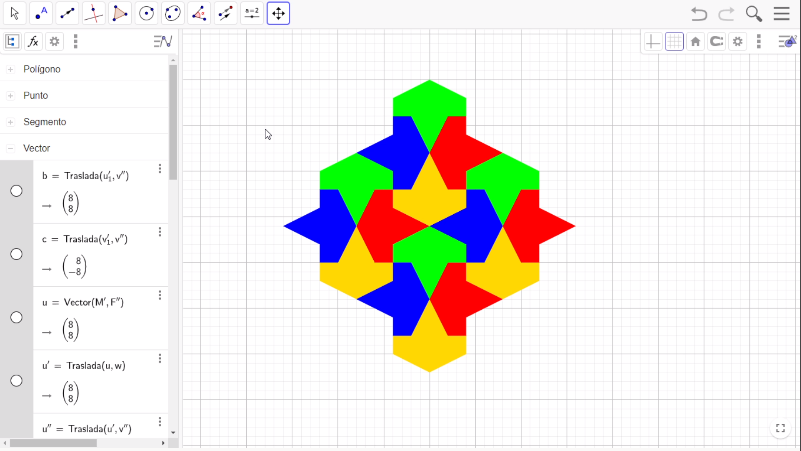
¡Listo! Concluiste el avión de Nazarí.
En esta sesión construiste teselados con ayuda de GeoGebra.
El reto de hoy:
Te invitamos a construir y crear tus propias teselaciones con ayuda de GeoGebra.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas