Proporcionalidad inversa VII
Proporcionalidad inversa VII
Aprendizaje esperado: analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: interpretar y resolver problemas que se modelan con este tipo de variación en diferentes contextos.
¿Qué vamos a aprender?
Hoy continuarás con el análisis y resolución de problemas de variación proporcional inversa. En esta ocasión resolverás problemas que se presentan en diversos contextos y que se modelan con este tipo de variación.
Ten a la mano tu cuaderno u hojas para tomar notas y tú lápiz o bolígrafo y una goma.
¿Qué hacemos?
Para iniciar, lee y analiza cuidadosamente el enunciado de cada uno de los problemas que se presentarán y piensa en una estrategia para resolverlos. Antes de aplicar un procedimiento, también es importante reflexionar sobre cuál es la propiedad o propiedades que se están usando para resolverlo.
Seguramente has escuchado acerca de las carreras de autos de la Fórmula 1. El primer problema que analizarás se ubica en ese contexto.

Una forma de iniciar la resolución del problema es reflexionar sobre las siguientes preguntas. Tú en casa, toma un tiempo para contestarlas.
¿La revisión la harán más o menos de 15 mecánicos?
Bien como vez, la revisión la harán menos de 15 mecánicos.
Los 5 mecánicos ¿deberían tardar más o menos de 600 segundos?
Los 5 mecánicos tardarán más de 600 segundos, que es lo que tardan 15 mecánicos.
¿La consigna y la pregunta se refieren a las mismas unidades de tiempo?
No. En los datos del problema se refiere a segundos y se pregunta por minutos.
¿Qué procedimiento pueden seguir para resolver el problema?
Anota lo que harían en tu cuaderno y resuelve el problema.
Ahora se revisarán dos maneras de resolver este problema.
Uno de los procedimientos es utilizar la constante de proporcionalidad inversa. Sin embargo, para estar en posibilidad de utilizarla es preciso que primero recuerdes qué es la constante de proporcionalidad inversa y cómo se obtiene.
El otro procedimiento es utilizar una proporción inversa. En este caso, debes saber lo que es una proporción de este tipo y cómo plantearla correctamente, incluso debes recordar qué es una proporción directa, porque se puede partir de ésta para facilitar el planteamiento de la inversa.

Se te invita a que reflexiones en lo que has aprendido a lo largo de este tema para responder las preguntas que se te plantean. Una vez que hayas reflexionado al respecto hay que aplicar ambos procedimientos.
En toda proporción inversa, al multiplicar los valores de la primera magnitud por su correspondiente de los de la segunda, se obtiene una constante, que se simboliza con la letra “k”.
En la siguiente tabla se muestran los valores de “x” y “y” de una proporción inversa. Ahí puedes ver que los productos de los valores correspondientes de cualquier fila, es 180; por ejemplo, 90 por 2, 30 por 6 y 10 por 18. Entonces 180 es la constante de proporcionalidad inversa para estos valores.
De manera general, la constante “k” es igual a “x” por “y”.
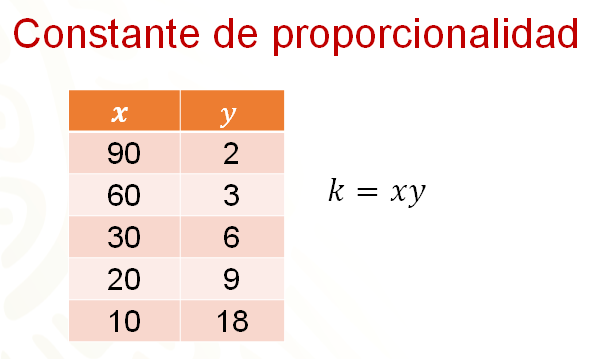
Primero se presentará el procedimiento utilizando la constante de proporcionalidad inversa. Hay que organizar los datos en una tabla, en donde anotas en la primera columna el número de mecánicos, que será la variable independiente, o sea “x”; en la segunda columna anotas el tiempo en segundos que tardan los mecánicos en hacer el trabajo; ésta será la variable dependiente, es decir, “y”.
Como la fórmula de la constante de proporcionalidad inversa es “k” igual a “x” por “y”, se sustituyen en ella los valores conocidos de “x” y “y”, por lo que “k” es igual a 15 por 600, lo que arroja como producto 9 000, que será el valor de la constante en este caso.
De la fórmula de la constante “k” igual a “x” por “y” se obtiene que “y” es igual a “k” entre “x”. Al sustituir en esta igualdad la constante y el valor de “x” igual a 5, se tiene que “y” es igual a 9000 entre 5, cuyo cociente es 1 800.
Con esto se puede afirmar que 5 mecánicos tardarían 1 800 segundos en hacer el mismo trabajo que 15 mecánicos realizan en 600 segundos.

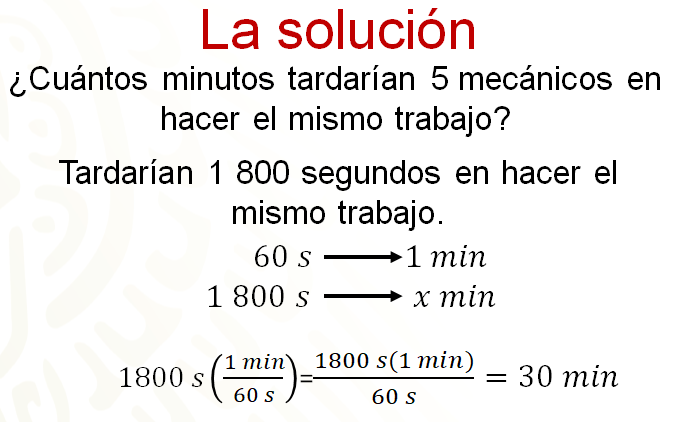
Ahora se pude dar solución al problema, es decir, contestar la pregunta ¿cuántos minutos tardarían 5 mecánicos en hacer el mismo trabajo?
Anteriormente se encontró que los 5 mecánicos tardarían 1 800 segundos en hacer el mismo trabajo.
Sin embargo, se pregunta por el tiempo en minutos, por lo tanto, se deben convertir los segundos en minutos. Sabes que 60 segundos equivalen a un minuto y quieres saber cuántos minutos son 1 800 segundos. Al resolver esta proporción directa, se multiplica 1 por 1 800 y el resultado se divide entre 60. Este último resultado es el número de minutos equivalentes a 1 800 segundos. Entonces, ¿cuántos minutos tardarían 5 mecánicos en hacer el mismo trabajo?
La respuesta es que tardarían 30 minutos.
Otro procedimiento que puedes usar es el que consiste en plantear dos razones para conformar una proporción inversa. Para facilitar formar la proporción inversa se puede partir de formar la proporción como si fuera directa. Así que, 15 es a 5 como 600 es a “y”, pero enseguida debes proceder a dejar la primera razón tal como está y se invierte la segunda, en lugar de escribir 600 es a “y”, escribes “y” es a 600. De esta manera se forma la proporción 15 es a 5 como “y” es a 600.
Para encontrar el valor de “y” se multiplica 15 por 600, entre 5. El resultado es 1 800, que es el mismo resultado al que se llega con el procedimiento anterior.

Es común cometer errores a la hora de plantear la proporción inversa. Para evitar confundirte, se puede plantear la proporción como si se tratara de una proporcionalidad directa, esto sólo con la finalidad de facilitar formar la proporción.

Revisa el caso de este problema. En la expresión del inciso “A” está planteada la proporción como si se tratara de proporcionalidad directa; luego, en el inciso “B” está formada la proporción inversa de forma correcta, ya que se mantuvo la primera razón y se invirtió la segunda.
Sin embargo, en el inciso “C”, aunque la proporción planteada es equivalente a la del inciso “A”, en el inciso “D” al invertir correctamente la segunda razón del inciso “C” la proporción inversa está mal planteada. El error surge porque en el inciso “C”, al plantear la proporción directa, no se respetó el colocar la misma clase de magnitud en la primera razón, en este caso, el número de mecánicos, sino que se formó con mecánicos y tiempo, por consecuencia, la proporción inversa planteada es incorrecta.
Dadas dos magnitudes inversamente proporcionales, la razón entre dos cantidades de la primera magnitud es igual a la razón inversa de las cantidades correspondientes de la otra. En la proporción del inciso “B” se observa que mientras una magnitud disminuye, la otra debe aumentar, por eso una flecha va hacia abajo y la otra hacia arriba.

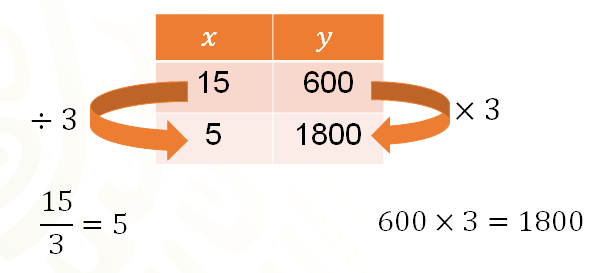
Otra propiedad de la variación proporcional inversa es que la razón entre dos cantidades de la primera magnitud es igual a la razón inversa de las cantidades correspondientes de la otra.
La siguiente tabla muestra cantidades que varían de manera inversamente proporcional. En ella se puede ejemplificar la propiedad enunciada anteriormente, ya que si “x” es igual a 15 y se divide entre 3 se obtiene “x” igual a 5, entonces a “y” igual a 600, que corresponde a “x” igual a 15, se multiplica por 3 para obtener el valor de “y” correspondiente a “x” igual a 1 800, como lo indican las flechas anaranjadas.
La razón inversa de 3 es , que es lo mismo que dividir entre 3 o viceversa.
Al resolver el problema de carreras de la Fórmula 1, se obtuvo que 5 mecánicos tardarían 30 minutos en hacer la revisión completa de uno de sus automóviles. Ahora se quiere saber ¿cuántos minutos tardarían 4, 8, 10 y 12 mecánicos en realizar el mismo trabajo?
Una forma de resolver el problema es construir una tabla donde, en la primera columna, se escriba el número de mecánicos que trabajarán en la revisión del automóvil y en la segunda, el tiempo (en minutos) que tardarán en hacer ese trabajo.
En el problema dice que 15 mecánicos realizan el trabajo en 600 segundos, que equivalen a 10 minutos, por eso, en la tabla se registró 10.

Se usa la fórmula de la constante “k” igual a “x” por “y” y si multiplicas cualquiera o las dos parejas de valores conocidos para “x” y “y”, es decir, 5 por 30 y 15 por 10, se obtiene que “k” es igual a 150.
Por otro lado, de la fórmula de la constante se obtiene que “y” es igual a “k” entre “x” se tiene que “y” igual a 150 sobre “x”. Entonces se utiliza esta expresión para obtener los valores correspondientes de “y” dividiendo 150 entre el valor de “x”, es decir, entre el número de mecánicos.
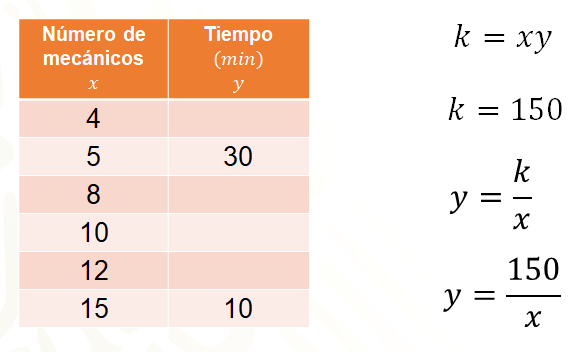
De esta forma se puede completar la tabla. Para 4 mecánicos “y” es igual a 150 entre 4, cuyo cociente es 37 punto cinco. Es decir, 4 mecánicos tardarían 37 punto 5 minutos en realizar el mismo trabajo.
En casa completa los datos que faltan en la tabla.
Ahora, compara tus resultados con los mostrados aquí y, en caso necesario, corrígelos.

- 8 mecánicos realizarían ese trabajo en 18 punto 75 minutos.
- 10 mecánicos realizarían ese trabajo en 15 minutos.
- 12 mecánicos realizarían ese trabajo en 12 punto 5 minutos.
Te puedes preguntar ¿qué procedimiento elegir?
Al resolver un problema de proporcionalidad inversa, utilizar la constante de proporcionalidad “y” igual a “k” entre “x”, o bien plantear una proporción inversa como la equivalencia de dos razones.
De hecho, es indistinto aplicar cualquiera de esos procedimientos, sin embargo, se debe notar que el problema inicial de las carreras de la Fórmula 1 se pedía un sólo valor, el correspondiente a la cantidad de tiempo que tardarían en la revisión 5 mecánicos, así que usar cualquier procedimiento es indistinto; sin embargo, en la segunda versión del problema, se pedían varios valores de la cantidad de tiempo, en esta última situación se vuelve más ágil utilizar la constante de proporcionalidad, ya que sólo se divide el valor de “k” entre los valores de “x” para encontrar los valores requeridos para “y”. Sería menos ágil formar proporciones inversas para cada valor.

Has revisado dos procedimientos con los cuales es posible resolver problemas de proporcionalidad inversa.
A continuación, se analizará y resolverá otro problema de este tipo de proporcionalidad a través de otro procedimiento.

Piensa en una estrategia para resolver este problema.
¿Ya la tienes?
Este problema puede resolverse con alguno de los dos procedimientos que ya se han utilizado, sin embargo, se revisará otra manera de resolver este tipo de situaciones.
En el problema que se está resolviendo, puede extraerse sólo lo matemático del enunciado, o sea, repartir 590 300 en partes inversamente proporcionales a 6, 8, 12 y 18. Ahora bien, recuerda una de las propiedades de la proporcionalidad inversa que dice: “dadas dos magnitudes inversamente proporcionales, la razón entre dos cantidades de la primera magnitud es igual a la razón inversa de las cantidades correspondientes a la otra”.
Utilizando esta propiedad sabes que repartir 590 300 en partes inversamente proporcionales a 6, 8, 12 y 18, equivale a repartir 590 300 en partes directamente proporcionales a un sexto, un octavo, un doceavo y un dieciochoavo.

Para resolver las proporciones directas se deben convertir las fracciones un sexto, un octavo, un doceavo y un dieciochoavo en sus equivalentes con igual denominador, éstas pueden ser, un sexto igual a 12, 72avos; un octavo igual a 9, 72avos; un doceavo igual a 6, 72avos, y un dieciochoavo igual a 4, 72avos.
Al sumar las fracciones, se obtiene 31/72, que es el total que hay que repartir entre los 4 hijos de forma directamente proporcional a las fracciones obtenidas. De ahí se forma la razón 590 300 es a 31/72, con las que se va a calcular la proporción directa.

Usando la primera fracción, 12, 72avos para plantear la proporción directa 590 300 es a 31/72 como “x” es a 12/72. Al resolver esta proporción directa, se obtendrá la cantidad que le corresponde a la primera fracción, es decir al hijo de 6 años.
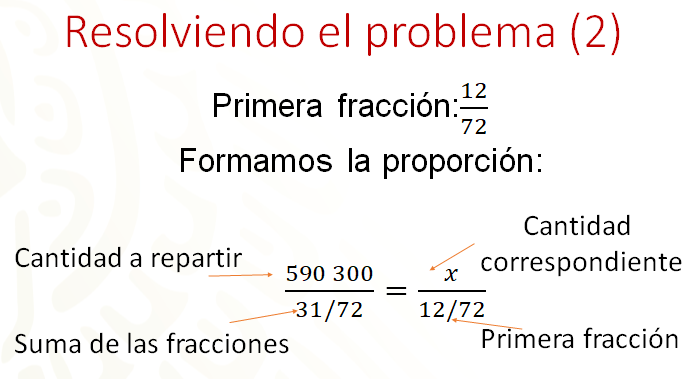
Para resolver la proporción directa que se ha planteado, en la siguiente imagen se tiene del lado izquierdo el procedimiento que conoces como regla de tres y que se basa en los productos cruzados, es decir, multiplicar 590 300 por 12/72 y dividirlo entre 31/72, de esa manera se obtiene 228 503 punto 22.
Del lado derecho se han usado los productos cruzados para formar una ecuación lineal, donde, al despejar “x” se encuentra el mismo resultado que en el procedimiento de la izquierda. Comparando ambos procedimientos te puedes dar cuenta que el procedimiento de la regla de tres se basa precisamente en el planteamiento de la ecuación.

Ambos procedimientos tienen su fundamento en una propiedad de las proporciones, el cual dice que el producto de los extremos es igual al producto de los medios, considerando a 590 300 y a 12/72 como los extremos, y a “x” y 31/72 los medios.
De esta manera, se puede decir que al hijo que tiene 6 años, le corresponden 228 503 pesos con 22 centavos.
Pon en práctica el procedimiento que has desarrollado para obtener la cantidad de dinero que le toca a cada uno de los demás hijos.
Recuerda que originalmente se está resolviendo una proporción inversa, pero en este caso se ha convertido en una proporción directa con el inverso de la segunda razón para llegar a la solución.
Ahora, se resolverá un último problema.

Cabe mencionar que se desea colocar toda la pintura en un sólo tipo de envase. En la tabla se muestran las diferentes capacidades que tendrán los envases, la idea es saber cuántos comprar, de acuerdo con la capacidad de los envases.
¿Qué harías para resolver este problema?
Podrías iniciar identificando ¿cuál es la consigna del problema?
Tienes que encontrar el número de recipientes de varias capacidades que se necesitan para envasar toda la pintura.
Por otro lado, ¿qué datos o condiciones se te proporcionan?
Primero, que hay 80 envases, cada uno con 5 litros de pintura. Luego, que se debe repartir toda la pintura en envases de dos, uno, medio o de un cuarto de litro.

Un procedimiento que se puede utilizar para resolver el problema es el uso de la constante “k”, que se obtiene multiplicando dos valores correspondientes conocidos, en este caso 5 por 80. El resultado de esta multiplicación es 400 por lo que se puede afirmar que “k” es igual a 400.
¿Qué representa el valor de “k” en el contexto de este problema?
Es el total de litros de pintura que se ha decidido colocar en envases de menor capacidad que en los que se encuentran.
Por otro lado, también se sabe qué “y” es igual a “k” entre “x”. Entonces sólo queda sustituir los valores que se tienen de “x”, es decir las diferentes capacidades, una por una, en esta expresión de “y”, para encontrar los diferentes valores de “y”, que es el número de envases requeridos. Por ejemplo, para “x” igual a 2 se tiene que “y” es igual 400 entre 2 igual a 200. Con esto, se sabe que se requieren 200 recipientes de 2 litros para envasar toda la pintura.
¿Cuántos envases de 1 litro se necesitan para envasar toda la pintura?
Se necesitan 400 envases de 1 litro.

Ya sabes que para envasar toda la pintura en recipientes de 2 litros se necesitan 200 de ellos. También se determinó que, si los envases son de 1 litro, entonces se requieren 400 de ellos.
Ahora, se va a calcular la cantidad de envases de medio litro que se necesitan para colocar en ellos toda la pintura.
Para ello, en “y” igual a 400 entre “x” se sustituye la “x” por un medio, por lo que tienes que “y” es igual a 400 entre un medio. Para resolver esta división, puedes utilizar el algoritmo de la división de fracciones y colocas un uno como denominador del 400. A continuación, se multiplica 400 por 2 y el resultado, que es 800, lo divides entre el resultado de uno por uno, es decir, entre uno. En este caso, “y” es igual a 800. Esto significa que, si se envasan los 400 litros de pintura en envases de medio litro, se necesitarán 800 envases de esta capacidad.
¿Cuántos envases se necesitan para envasar los 400 litros en envases de a un cuarto de litro?
Realiza los cálculos necesarios. ¿Cuánto obtuviste?
Para envasar toda la pintura en envases de un cuarto de litro se necesitan 1 600 de estos recipientes.

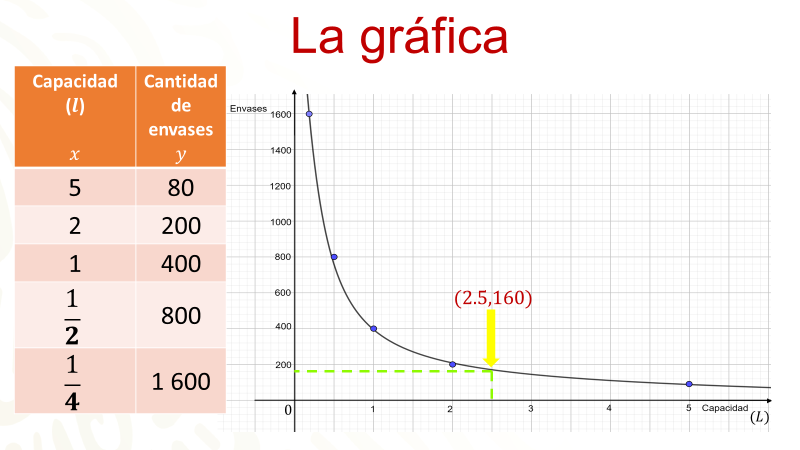
Es posible presentar en una gráfica el problema de los envases. Se hace a partir de los valores de la capacidad de los envases y el número de ellos que se requieren. Estos valores se representan en una tabla.
La gráfica que representa este problema, llamada hipérbola, se comporta de esta manera: mientras la capacidad del envase aumenta, la cantidad de envases disminuye, esto equivale a decir que mientras la curva se acerca más al eje “x”, los valores en el eje “y” serán menores. En el eje “y”, mientras mayor es la cantidad de envases, la capacidad de ellos será menor, es decir que mientras más se acerca la curva al eje “y”, los valores de “x” serán menores.
Pero ¿tiene sentido envasar pintura en recipientes de capacidad cero litros? La respuesta es no, y por ello la curva no toca el eje “y”, porque la “x” seria cero, y esto no tendría sentido.
En la misma gráfica se muestra la coordenada 2 punto 5 coma 160. ¿Qué significa esta coordenada en el contexto del problema?
Es cuando una coordenada se puede determinar exactamente en la gráfica, es posible encontrar otros valores para “x” y para “y”, en este caso, esa coordenada indica que, cuando los envases tienen una capacidad de 2 punto 5 litros, se requieren 160 de ellos para colocar 400 litros de pintura.
Si necesitas aclarar dudas, recurre a otras fuentes de información acerca del tema, sobre todo, consulta tu libro de texto.
El reto de hoy:
El reto del día hoy, consiste en que utilices el mismo procedimiento que se usó en el problema de la herencia para obtener la cantidad de dinero que le corresponde a cada uno de los hijos que faltó calcular. Recuerda que sólo se calculó la cantidad que le corresponde al hijo de 6 años y que es de 228 503 pesos con 22 centavos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas