Método de sustitución
Método de sustitución
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: resolver problemas mediante el planteamiento y la solución de sistemas de dos ecuaciones lineales con dos incógnitas utilizando el método de sustitución.
¿Qué vamos a aprender?
En esta sesión resolverás problemas mediante el planteamiento y solución de sistemas de dos ecuaciones lineales con dos incógnitas utilizando el método de sustitución.
En las situaciones que abordarás utilizarás las literales “x” y “y” para representar datos desconocidos en ambas ecuaciones, es decir, las incógnitas, por lo tanto, el valor de “x” y “y” es el mismo en la primera y en la segunda ecuación.
En estos problemas se tratará de determinar el costo de diversos productos.
¿Qué hacemos?
Para iniciar recuerda que, para resolver un sistema de dos ecuaciones lineales con dos incógnitas con el método de sustitución, debes realizar una serie ordenada de pasos. Anota tus reflexiones y tus respuestas a los problemas, así como las dudas que te vayan surgiendo.
Ahora se revisará la siguiente situación.
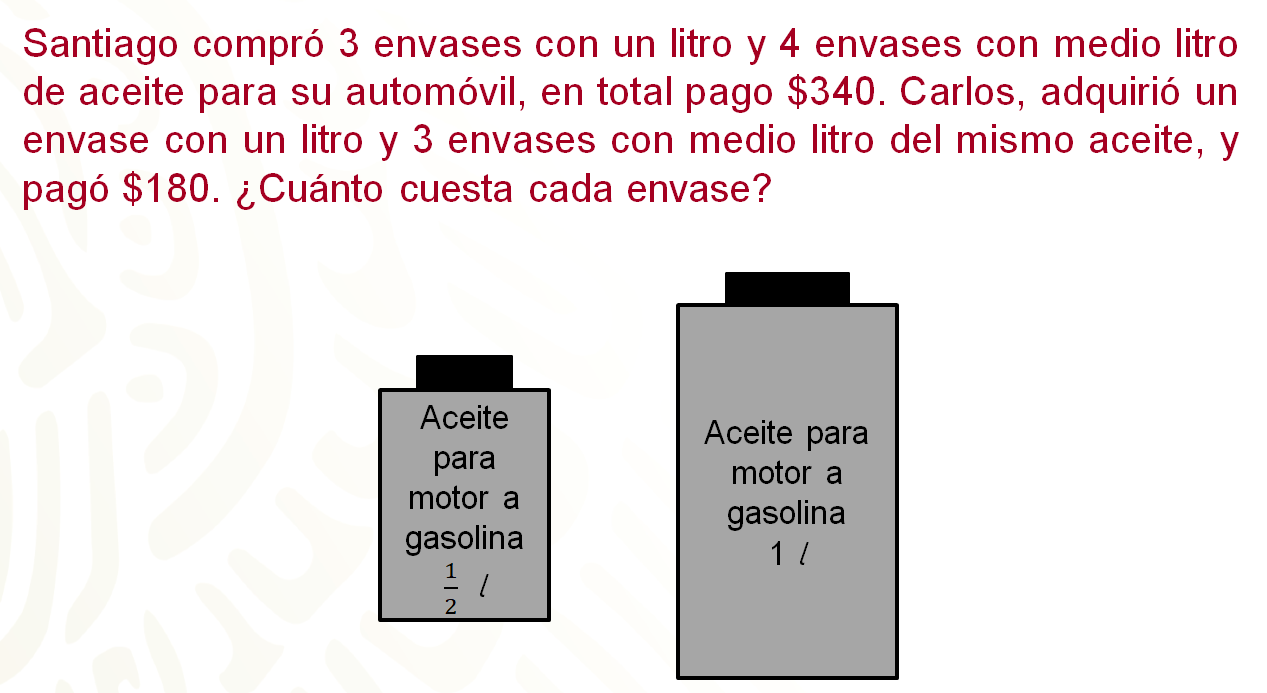
Realiza y anota una estimación del costo de cada envase con aceite. ¿Ya la anotaste?
Una manera de iniciar la resolución del problema es contestar ¿Cuáles son las incógnitas?
Se les llamará “x” y “y” a las incógnitas.
De acuerdo con la situación de Santiago y Carlos se puede determinar que “x” representa el costo de un envase con un litro de aceite y “y” el costo de un envase con medio litro de aceite, aunque también se podría asignar esas literales al revés.

Ahora, el siguiente paso consiste en el planteamiento del sistema de ecuaciones lineales, con base en los datos incluidos en el enunciado de la situación. Escribe en tu cuaderno el sistema de ecuaciones que piensas y modela este problema.

La ecuación 1 representa la compra que realizó Santiago.
Ésta es 3 “x” más 4 “y” igual a 340. Porque 3 “x” representa 3 por el costo de un envase con 1 litro de aceite, a lo que hay que sumar lo que representa 4 “y”, es decir 4 por el costo de un envase con medio litro de aceite. Esa suma es igual a 340, que es lo que pagó Santiago por su compra.

Ahora, se nombrará la ecuación 2 que representa la compra de Carlos. Ésta es “x” más 3 “y” igual a 180.
Porque Carlos compró un envase con 1 litro de aceite, que es “x” más 3 envases con medio litro, que se representa como 3 “y” y por su compra pagó 180 pesos.
Pero, te has preguntado ¿por qué estas ecuaciones forman un sistema?
Esto ocurre porque el costo de un envase con un litro de aceite es el mismo en la compra de Santiago que en la de Carlos. Lo mismo ocurre para el caso del costo del envase con medio litro de aceite.
Por lo tanto, el sistema de dos ecuaciones lineales con dos incógnitas que permite resolver esta situación es 3 “x” más 4 “y” igual a 340 y “x” más 3 “y” igual a 180.

¿Qué piensas que puedes hacer a continuación para calcular el valor de “x” y el de “y”?
Para aplicar el método de sustitución se debe despejar una de las incógnitas en alguna de las ecuaciones del sistema. Piensa ¿Qué incógnita, “x” o “y” es más fácil de despejar en alguna de estas ecuaciones?
En este caso, puedes observar que la “x” de la ecuación 2 presenta mayor facilidad para despejar dado que su coeficiente es uno y los demás términos con incógnita tienen coeficientes diferentes de uno.
Entonces, se despeja la incógnita “x” en la ecuación 2.
Puedes aplicar el inverso aditivo de 3 “y” en ambos miembros de la ecuación. Al realizarlo se obtiene 3 “y” negativo más “x” más 3 “y” igual a 180 menos 3 “y”.
De tal forma que, al suprimir 3 “y” negativo” más 3 “y” porque su suma es cero, se obtiene “x” igual a 180 menos 3 “y”, que también lo puedes escribir como “x” es igual a 3 “y” negativo más 180.

A continuación, se sustituye el valor encontrado para “x” en la ecuación 1. Es decir, se despeja una incógnita en una ecuación y se sustituye en la otra.
De esta manera, la ecuación adquiere la forma 3 por, abre paréntesis, 3 “y” negativo más 180, cierra paréntesis, más 4 “y” igual a 340.
Para calcular el valor de “y”, se debe despejar esta incógnita. Hay a hacerlo.
Aplicas la propiedad distributiva de la multiplicación con respecto a la suma y obtienes 9 “y” negativo más 540, más 4 “y” igual a 340. Luego, se reducen los términos semejantes 9 “y” negativo con más 4 “y” y, al mismo tiempo restas 540 en ambos miembros de la ecuación, obteniendo 5 “y” negativo más 540, menos 540 es igual a 340 menos 540.
De lo anterior se obtiene 5 “y” negativo igual a 200 negativo. Para continuar divides ambos miembros entre 5 negativo para obtener el coeficiente uno para “y”. Así que la ecuación es 5 “y” negativo entre 5 negativo igual a 200 negativo entre 5 negativo.
Ahora, al dividir 5 “y” negativo entre 5 negativo se obtiene uno “y”, y al dividir 200 negativo entre 5 negativo se obtiene 40.
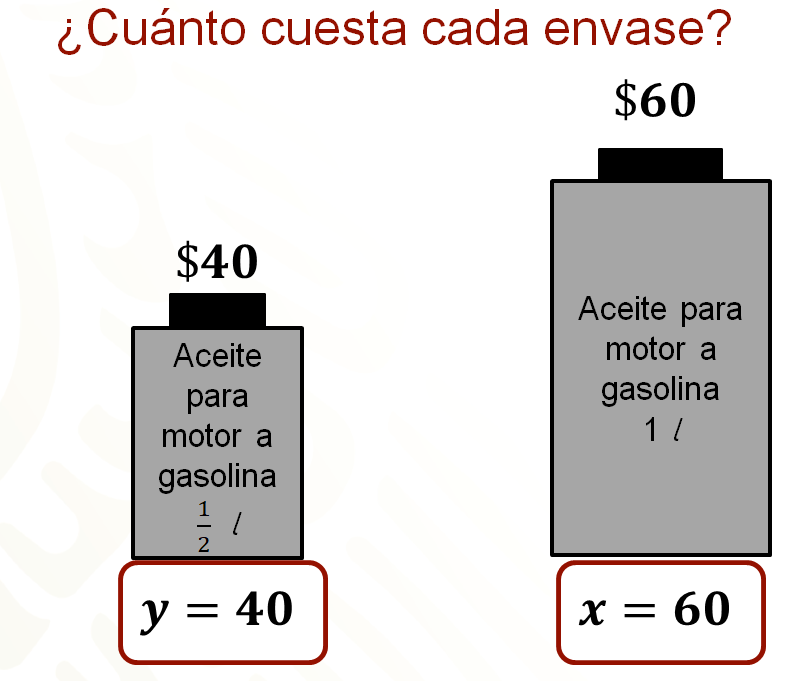
Así se obtiene “y” igual a 40.

¿Qué significa este 40 en el contexto del problema?
40 representa el costo del envase con medio litro de aceite.
Una vez que se obtiene el valor de una incógnita, en este caso “y”, puedes sustituir este valor en el despeje de la otra, es decir en el despeje que se hace de “x”.
Al despejar “x” anteriormente, se obtuvo “x” es igual a 3 “y” negativo más 180. Sustituyendo se tiene “x” igual a 3 negativo por 40, más 180. De ahí que “x” es igual a 120 negativo más 180.
Luego, como 120 negativo más 180 es igual a 60, entonces, “x” es igual a 60.

¿Qué significa este valor de “x” en este problema?
60 representa el costo del envase con un litro de aceite.
Pero ¿cómo puedes estar seguro o segura, que los valores encontrados para “x” y para “y” son los que resuelven correctamente el problema?
Se puede hacer la comprobación en las ecuaciones del sistema.
Se iniciará con la comprobación en la ecuación 1.
Para ello, se sustituyen los valores de “x” y “y”, en la ecuación 3 “x” más 4 “y” igual a 340.
Ahora tienes 3 por 60, más 4 por 40, igual a 340. Como 3 por 60 es igual a 180 y 4 por 40 es igual a 160, tienes 180 más 160 igual a 340. Al resolver la suma tienes que 180 más 160 es igual a 340. Puedes observar que 340 es igual a 340 y puedes afirmar que dichos valores hacen verdadera la igualdad.

A continuación, se llevará a cabo la comprobación en la ecuación 2 que es “x” más 3 “y” igual a 180.
Como se obtuvo que “x” es igual a 60 y “y” igual a 40, al efectuar la sustitución se obtiene 60 más, 3 por 40 igual a 180.
Como 3 por 40 es igual a 120, tienes que 60 más 120 es igual a 180.
La suma de 60 y 120 es igual a 180 por lo que tienes 180 igual a 180. Como puedes observar, los valores que se obtuvieron para “x” y para “y” también hacen verdadera la ecuación 2.
Por lo tanto, se afirma que los valores de “x” y “y” son correctos.

Para terminar, hay que responder la pregunta del problema: ¿cuánto cuesta cada envase? Seguramente tú ya tienes la respuesta correcta.
El costo de un envase con medio litro de aceite es de 40 pesos y el costo de un envase con 1 litro de aceite es de 60 pesos.
Regresa a la estimación que se hizo al inicio de la resolución del problema, ¿qué tan acertada fue?
¿Cómo vas? Recuerda anotar todas tus reflexiones y tus dudas. Hay que analizar otra situación.

¿Qué datos te piden calcular para dar respuesta al problema?, ¿Cómo se pueden representar esos datos?, ¿Qué sistema de ecuaciones lineales te permite determinar los valores desconocidos?
Lo que se te solicita calcular es el costo de los dos tipos de boletos y una forma de representarlos es a través de literales que representen esas incógnitas.
Hay que ir a la resolución del problema, que te llevará al planteamiento del sistema de ecuaciones y, posteriormente, a la respuesta del problema.
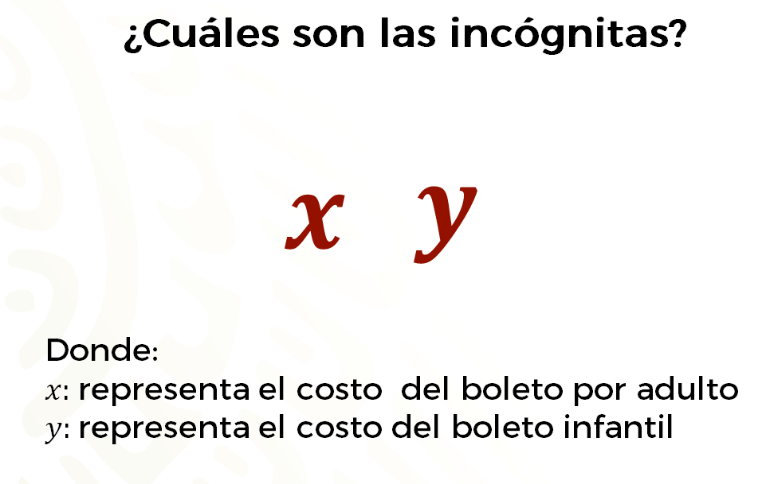
¿Cuáles son las incógnitas?
Puedes utilizar las literales “x” y “y” para representar los datos desconocidos, es decir, a las incógnitas, de acuerdo con la situación de las familias que visitaron el museo se determinará que, “x” representa el costo del boleto por adulto y “y” el costo del boleto infantil. También se puede establecer que “x” represente el costo del boleto infantil y “y” represente el costo del boleto por adulto.
De acuerdo con la situación, ya se estableció a “x” como el costo del boleto por adulto y “y” como el costo de boleto infantil. Ahora, se puede plantear el sistema de ecuaciones lineales que modela la situación lo que te llevara a dar respuesta a la pregunta ¿Qué sistema de ecuaciones lineales te permite determinar los valores desconocidos?
Se va a plantear la ecuación 1 que corresponde a la familia de Raquel que adquirió un boleto de adulto y 4 infantiles.
Seguramente pensaste en la ecuación, “x” más 4 “y” igual a 545, ya que esa familia adquirió un boleto de adulto y cuatro infantiles, por los que se pagó 545 pesos.

¿Qué ecuación corresponde a la familia de Verónica que compró dos boletos de adulto y tres infantiles?
La ecuación es 2 “x” más 3 “y” igual a 565, ya que esta familia al comprar dos boletos de adulto y tres infantiles pagó 565 pesos.

Estas dos ecuaciones integran un sistema ya que hay una relación entre el costo de los boletos por adulto con el costo de los boletos infantiles y la cantidad que pagará cada familia.
Por lo tanto, el sistema de dos ecuaciones lineales con dos incógnitas que permite resolver la situación es “x” más 4 “y” igual a 565 que es la ecuación 1 correspondiente a la familia de Raquel y 2 “x” más 3 “y” igual a 565, que es la ecuación 2 correspondiente a la familia de Verónica.

¿Recuerdas cuál es el siguiente paso?
Ahora, debes despejar una de las incógnitas en cualquier ecuación.
¿En qué ecuación despejarías la incógnita?, ¿Qué incógnita despejarías?, ¿Por qué elegirías esa incógnita?
En este caso, la incógnita que puede ser más fácil de despejar es la “x” en la ecuación 1, dado que su coeficiente es uno y los demás términos con incógnita tienen coeficientes diferentes de uno.
Entonces, despeja “x” en la ecuación 1.
La ecuación es “x” más 4 “y” igual a 545.
Puedes restar 4 “y” en ambos miembros de la ecuación, de manera que tienes 4 “y” negativo más “x” más 4 “y” igual a 545 menos 4 “y”.
Suprimes 4 “y” negativa con más 4 “y” del primer miembro de la ecuación porque su suma es cero, obteniendo “x” igual a 545 menos 4 “y” que también puedes escribir como “x” igual a 4 “y” negativo más 545.

A continuación, sustituyes el valor encontrado para “x” en la ecuación 2. De esta manera, tienes 2 por, abre paréntesis, 4 “y” negativo más 545, se cierra paréntesis, más 3 “y” igual a 565.
Para calcular el valor de “y”, se debe despejar esta incógnita. Hay que hacerlo. Aplicas la propiedad distributiva de la multiplicación con respecto a la suma y obtienes 8 “y” negativo más 1,090, más 3 “y” igual a 565. Luego, reduces los términos semejantes 8 “y” negativo con más 3 “y” por lo que la ecuación resultante es 5 “y” negativo más 1,090 igual a 565.
A continuación, restas 1,090 en ambos miembros de la ecuación, quedando 5 “y” negativo más 1,090, menos 1,090 es igual a 565 menos 1,090.
Al resolver las operaciones tienes 5 “y” negativo igual a 565 menos 1,090, conduciendo a 5 “y” negativo igual a 525 negativo.
Para continuar divides ambos miembros entre 5 negativo para obtener el coeficiente uno para “y”. Así que la ecuación es 5 “y” negativo entre 5 negativo igual a 525 negativo entre 5 negativo.
Ahora, al dividir 5 “y” negativo entre 5 negativo se obtiene uno “y”, y al dividir 525 negativo entre 5 negativo se obtiene 105.
Así, se obtiene “y” igual a 105.

¿Qué representa este valor de “y” en el problema que se está resolviendo?
105, representa el costo, en pesos, del boleto por infante.
¿Qué hacemos a continuación?
Ahora, sustituyes el valor de “y” en el despeje de “x”.
Si “x” es igual a 4 “y” negativo más 545, al sustituir “y” igual a 105, tienes “x” igual a 4 negativo por 105 más 545. El producto de 4 negativo por 105 es 420 negativo, entonces “x” es igual a 420 negativo más 545. La suma es igual a 125, por lo tanto, “x” es igual 125. Este valor corresponde al costo, en pesos, del boleto por adulto.

Pero ¿cómo puedes estar seguro o segura de que los resultados que obtuviste son correctos?
Puedes comprobar estos resultados en las ecuaciones del sistema que obtuviste para este problema.
Inicia con la comprobación en la ecuación 1.
Para ello, sustituyes los valores de “x” y “y”, en la ecuación “x” más 4 “y” igual a 545.
Ahora tienes 125 más, 4 por 105, igual a 545. Como 4 por 105 es igual a 420, tienes 125 más 420 igual a 545. Al resolver la suma tienes que 125 más 420 es igual a 545.
Puedes observar que 545 es igual a 545 y puedes afirmar que dichos valores hacen verdadera la igualdad.

Ahora, se llevará a cabo la comprobación en la ecuación 2 que es 2 “x” más 3 “y” igual a 565.
Como se obtuvo que “x” es igual a 125 y “y” igual a 105, al efectuar la sustitución obtienes 2 por 125, más 3 por 105 igual a 565.
2 por 125 es igual a 250 y 3 por 105 es igual a 315, tienes 250 más 315 es igual a 565.
La suma de 250 y 315 es igual a 565 por lo que tienes 565 igual a 565. Como puedes observar, los valores que obtuviste para “x” y para “y” también hacen verdadera la ecuación 2.

Por lo tanto, se afirma que los valores de “x” y “y” son correctos.
Para concluir esta situación responde: ¿Cuánto cuesta cada boleto?
El costo del boleto por adulto es de 125 pesos y el costo del boleto infantil es de 105 pesos.

¿Cómo vas hasta aquí?, ¿Has anotado tus dudas? Recuerda que es importante hacerlo para consultarlas posteriormente con tu maestra o maestro de esta asignatura.
Hay que resolver otro problema más.

Hay que usar ahora “w” y “z” para representar las incógnitas. De manera que “w” representa el costo de un cuaderno, “z” representa el costo de un bolígrafo.

De acuerdo con estas representaciones de las incógnitas y sabiendo que Miguel compró dos cuadernos y dos bolígrafos por 60 pesos. María adquirió tres cuadernos y un bolígrafo de la mismas marcas y precios que Miguel, pero ella pagó 74 pesos, anota en tu cuaderno, el sistema de ecuaciones que modela este problema.
El sistema de ecuaciones está formado por:
Ecuación 1: lo que compró Miguel, que se representa como 2 “w” más 2 “z” igual a 60.
Y la ecuación 2: lo que compró María, 3 “w” más “z” igual a 74.

¿Qué se hace a continuación?
Despejar una de las incógnitas. ¿Cuál es más conveniente?
Sería más fácil despejar “z” en la ecuación 2. Hay que hacerlo.
En 3 “w” más “z” igual a 74, sumas el inverso aditivo de 3 “w”, es decir 3 “w” negativo en ambos miembros de la ecuación, para suprimirlos en el primer miembro.
Esto genera la ecuación “z” igual a 74 menos 3 “w”, o su equivalente “z” igual a 3 “w” negativo más 74.

Como se despejó “z” en la ecuación 2, entonces, se sustituye su valor en la ecuación 1, por lo que se tiene 2 “w” más 2, abre paréntesis, 3 “w” negativo más 74, cierra paréntesis, igual a 60.
Aplicando la propiedad distributiva de la multiplicación con respecto a la suma, se tiene 2 “w” menos 6 “w”, más 148 igual a 60.
De ahí se obtiene que 4 “w” negativo es igual a 88 negativo.
Ahora, dividiendo ambos miembros entre 4 negativo, se obtiene que “w” es igual a 22.

Ahora se sustituye el valor de “w” en la expresión “z” igual a 3 “w” negativo más 74, por lo tanto, “z” es igual a 3 negativo por 22 más 74, de donde “z” es igual a 66 negativo más 74, y finalmente, “z” es igual a 8.

¿Cuál es el costo de un cuaderno?, y ¿cuál es el costo de un bolígrafo?
Sí “w” es igual a 22, y “w” representa el costo de un cuaderno, entonces cada cuaderno tiene un costo de 22 pesos.
Sí “z” es igual a 8, y representa el costo de un bolígrafo, se puede afirmar que el costo de un bolígrafo es de 8 pesos.

¡Terminaste con este tercer problema!
Recuerda que, en esta sesión, se dio solución a problemas partiendo de plantear y resolver un sistema de ecuaciones lineales con dos incógnitas, mediante el método de sustitución.
El reto de hoy:
En tu cuaderno formula un problema que se resuelva con un sistema de dos ecuaciones lineales con dos incógnitas, resuélvelo con el método de sustitución y describe cómo lo resolviste.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas