¿Qué número sigue?
¿Qué número sigue?
Aprendizaje esperado: identifica la regularidad en sucesiones con números (incluyendo números fraccionarios) que tengan progresión aritmética, para encontrar términos faltantes o continuar la sucesión.
Énfasis: determina la regularidad de una sucesión con progresión aritmética y la aplica para encontrar términos faltantes o continuar la sucesión.
¿Qué vamos a aprender?
Identificarás la regularidad en sucesiones con números, incluyendo números fraccionarios que tengan progresión aritmética, para encontrar términos faltantes o continuar la sucesión.
¿Qué hacemos?
En la sesión de hoy seguirás trabajando con sucesiones de números, practicaremos y abundaremos en las sucesiones y buscaremos valores faltantes.
En matemáticas siempre encontrarás que mientras más apliques el conocimiento en la resolución de problemas, cada vez encontrarás mayor facilidad para identificar los caminos.
Las sucesiones numéricas pueden representar diversas situaciones hasta de nuestra vida cotidiana, también son muy importantes en la industria para tener el control de los productos, para un tratamiento médico y hasta en la naturaleza.
Las sucesiones numéricas tienen muchos usos, pero antes de empezar con nuestras actividades de la sesión de hoy, recuerda algo importante que para determinar que una lista de números se considere sucesión tenemos que establecer o definir un patrón o regularidad entre los términos de la sucesión y ese patrón lo podemos hacer sumando y restando entre cada término, para las sucesiones, dependiendo de la situación.
En nuestra clase vamos a encontrar el patrón en las fracciones, pon mucha atención, también te invito que vayas realizando las actividades con nosotros.
Iré haciendo unas preguntas de sucesiones numéricas. Observa, analiza y contesta. La primera pregunta para empezar es:
- Si iniciamos en el número 9 y los demás términos se obtienen sumando 8 al término anterior, di cuáles son los primeros 5 términos.
Si comenzamos en 9 el siguiente es 17 luego 25 le sigue el 33 y el quinto término es el 41 entre estos números la constante es 8 es decir, se suma 8 al término anterior para obtener el siguiente.
Realicemos éste otro, fíjate bien: - ¿Cuáles son los primeros 5 términos de una sucesión si inicia en 4 y la diferencia entre dos términos consecutivos es 14?
Como la diferencia entre término y término es 14, a 4 le sumo 14 y así a cada uno de los siguientes, los primeros términos de la serie que van de 14 en 14 y que empieza en 4 son, 4, 18, 32, 46 y 60.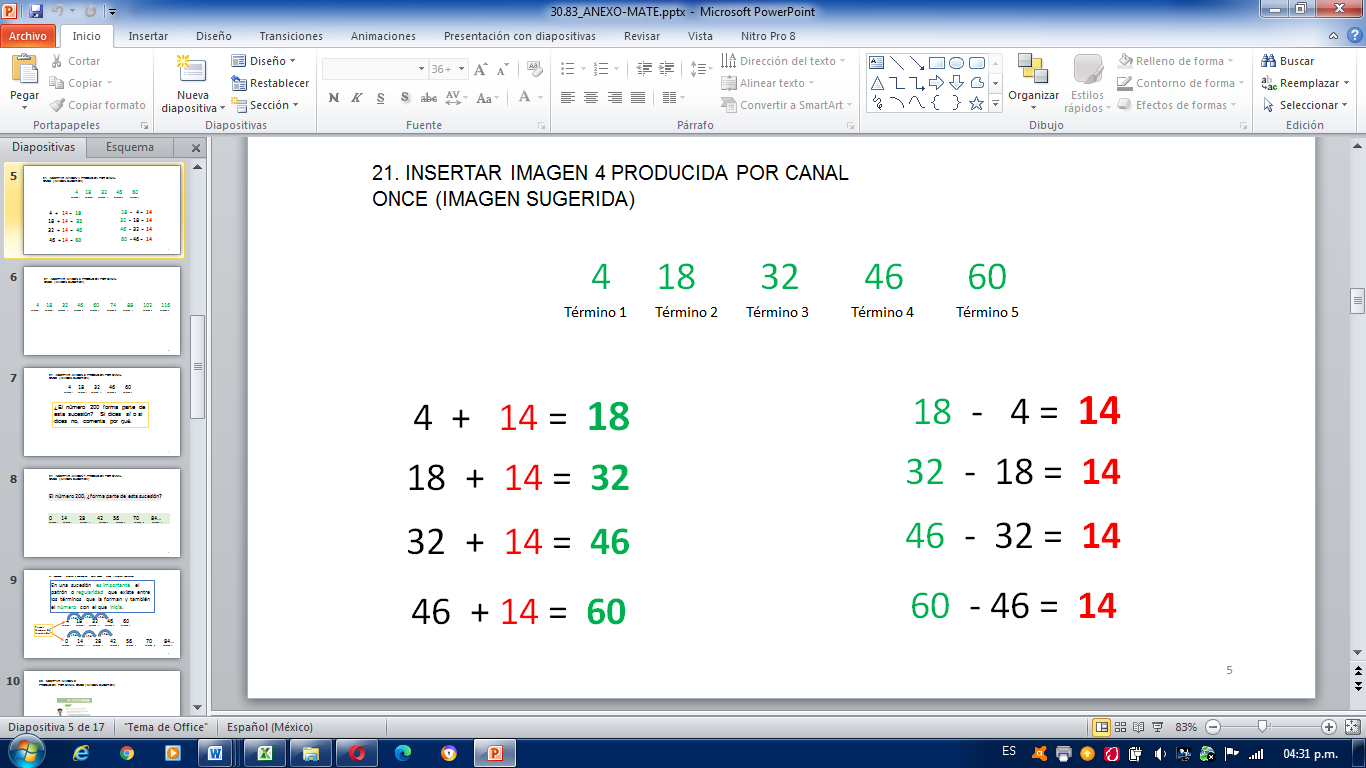
En esta sucesión que acabamos de escribir, qué número será el noveno término. Como el sesenta fue el quinto término, para saber la respuesta, debes continuar la sucesión, así que el sexto término es 74, el séptimo es 88, el octavo es 102 y el noveno es 116
Vamos a responder y a explicar la siguiente pregunta que dice: - ¿El número 200 forma parte de esta sucesión? Si dices sí o si dices no, comenta por qué.
Si seguimos sumando 14 a partir del 116 llegamos al 200 entonces el 200 forma parte de la sucesión anterior y si sigo sumando 14, al número anterior en esa sucesión encuentro el 200 - Ahora fíjate en esta sucesión y dime si 200 es parte de ella.
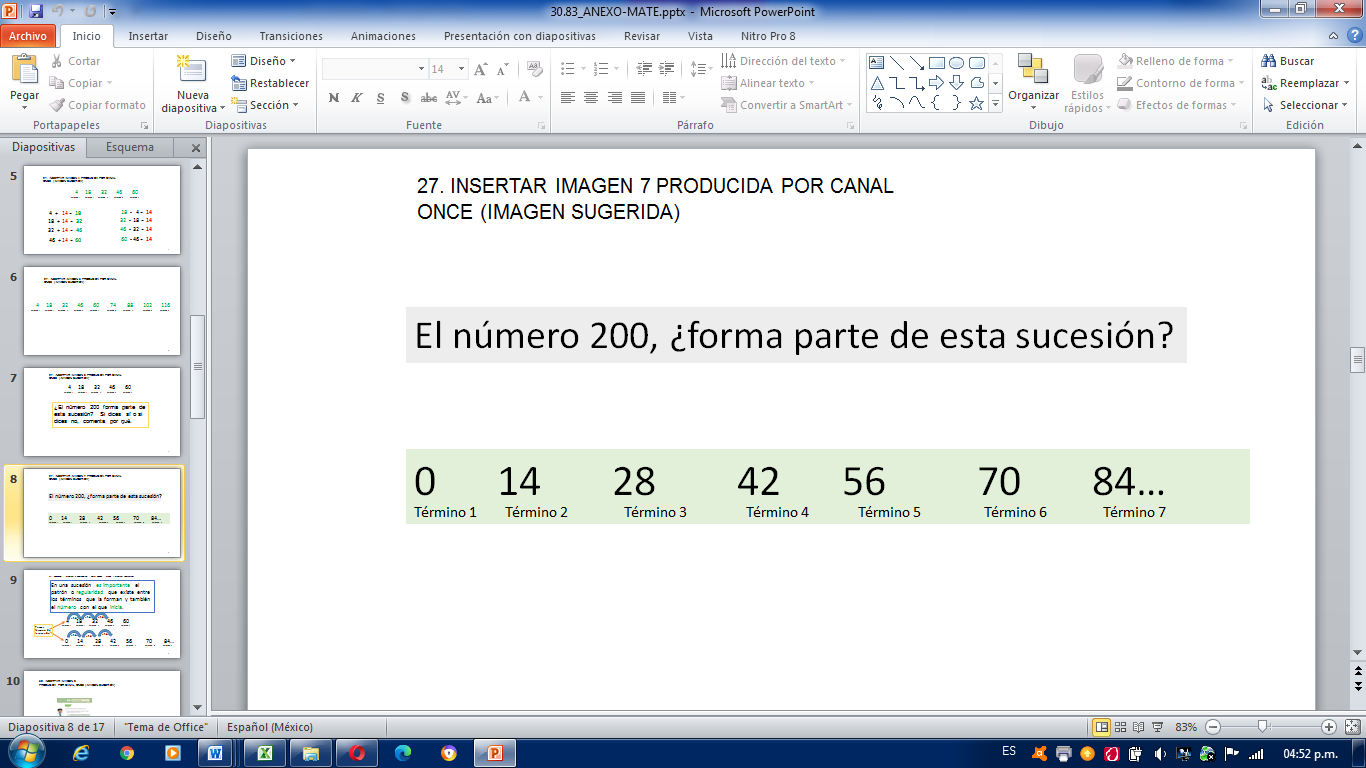
Lo puedes hacer con la calculadora 0, 14, 28, 42, 56, 70, 84, 98, 112, 126, 140, 154, 168, 182, 196, 210, no salió 200 si entre un término y el siguiente se suman 14 igual que en la sucesión anterior.
Ya compararon las dos sucesiones. ¿Cuál creen que sea la diferencia entre ellas, si en ambas se suman 14 para obtener el término siguiente?
Observa bien, aunque en las dos sucesiones sumamos 14 al término anterior para obtener el siguiente, la primera sucesión comenzó en 4 y la segunda sucesión comenzó en 0 entonces no son iguales estas sucesiones y por eso salen términos diferentes, aunque el patrón o regularidad sea la misma.
En una sucesión no solamente es importante la regularidad o patrón que permite encontrar los números que la forman, también es importante el primer número, es decir, el número con el que comienza.
Pasemos a esta otra sucesión, ahora no sólo debes saber cuál es la regularidad, también debes encontrar los términos que faltan. - 6, __, 28, 39, 50, ____, 72, ___, 94
Lo primero que hice fue ubicar dos números consecutivos y restarlos, aquí tomé 50 menos 39 y encontré que son 11 luego también revisé cuánto me daba 39 menos 28 y también me dio 11 así ya tenía que el patrón o regularidad entre estos números debe ser 11, por lo que podía seguir dos caminos para encontrar los números que faltan. Uno era sumar 11 al anterior y el otro era restar 11 al que le seguía. Yo escogí el primero y sumé 11 para obtener que los números faltantes son: 17, 61 y 83
Ahora vamos a resolver el desafío número 62 “Uso de patrones” que se encuentra en la página 118 de tu libro de Desafíos Matemáticos.
El primer planteamiento dice así:
- ¿Cuál de las siguientes descripciones corresponde a la regularidad de la sucesión un medio, uno, tres medios, dos, cinco medios y tres?
Aquí hay números enteros y fracciones comunes, para que sea más fácil, voy a convertir todo en fracciones con igual denominador, es decir, voy a escribir los enteros como fracciones que tengan como denominador el 2 entonces la sucesión queda como un medio, dos medios, tres medios, cuatro medios, cinco medios y seis medios. La constante entre cada término es de un medio, por lo tanto, la opción correcta es la última que está en la tabla, que dice: la regularidad es que cada término se determina aumentando un medio al término anterior.
La siguiente pregunta dice: - ¿Cuál es la regularidad de la siguiente sucesión, un dieciseisavo, cinco dieciseisavos, nueve dieciseisavos y trece dieciseisavos?
Aquí todas las fracciones son dieciseisavos, y la regularidad es que cada término se determina aumentando cuatro dieciseisavos al término anterior.
La siguiente pregunta dice: - ¿Cuál es el término que le falta en la siguiente sucesión, un octavo, un cuarto, tres octavos, el término que falta y cinco octavos?
Si convertimos un cuarto a octavos, serán dos octavos, quedaría la sucesión un octavo, dos octavos, tres octavos, el término que falta y cinco octavos, por lo tanto, el término que falta es cuatro octavos.
Ahora voy a compartirles otra forma para obtener ese término, si sumamos un octavo al primer término tenemos dos octavos, pero dos octavos es igual que un cuarto. Luego, vuelvo a sumar un octavo y me dan 3 octavos, si sumo un octavo me dan los 4 octavos, pero sabemos que 4 octavos es lo mismo que 2 cuartos, así que, si pusieron 2 cuartos, también es correcto. Y podemos ver que, si sumamos otra vez un octavo, tenemos 5 octavos, así que vamos bien, anoté dos términos más y mi sucesión quedó así:
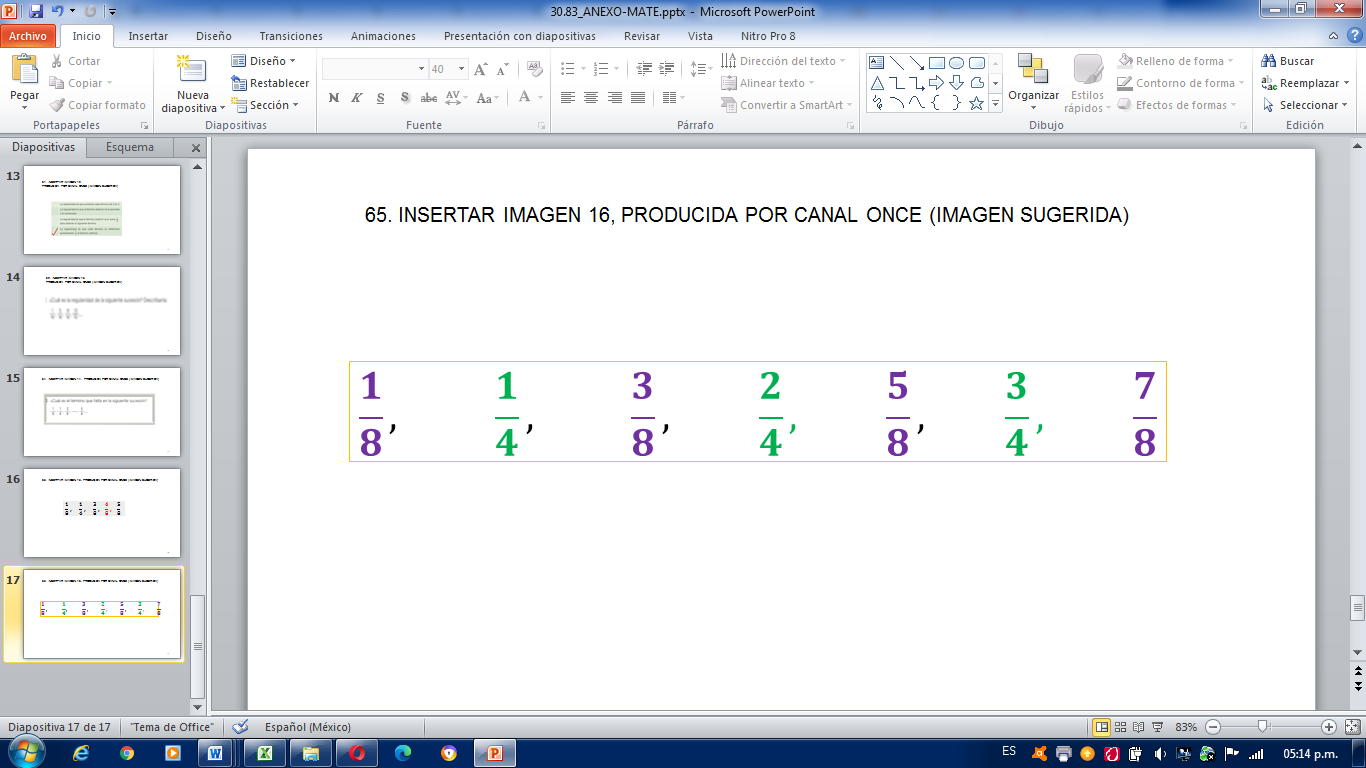
Sin hacer operaciones puedo continuar esa sucesión.
Los 4 términos siguientes después de 7 octavos, sigue 4 cuartos, luego, 9 octavos, después 5 cuartos, y luego 11 octavos.
Recordemos qué fue lo que estudiamos en la sesión de hoy: Encontramos la regularidad de una sucesión, con lo pudimos conocer qué números seguían o faltaban en la sucesión, pero también vimos que es muy importante conocer el primer término de la sucesión además de la regularidad entre los términos, así pudimos determinar por qué un número puede ser parte de una sucesión que tiene la misma regularidad que otra y no estar en esta otra.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
