Método gráfico
Método gráfico
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: resolver problemas mediante el planteamiento y solución de sistemas de dos ecuaciones lineales con dos incógnitas utilizando el método gráfico.
¿Qué vamos a aprender?
Esta sesión será práctica, profundizaremos en el estudio de los métodos de solución para un sistema de ecuaciones de 2 incógnitas con 2 ecuaciones, concretamente estudiaremos el método gráfico.
Durante el estudio de las matemáticas en segundo grado de secundaria, concretamente con el estudio del álgebra, existen varios métodos para resolver un sistema de 2 ecuaciones lineales con 2 incógnitas.
Si en cada paso de cualquiera de esos métodos, realizamos las operaciones correctamente, llegaremos a las soluciones que cumplen adecuadamente las condiciones de las 2 ecuaciones. En esta sesión realizaremos trazos, leeremos la solución del sistema de ecuaciones en una gráfica, incluso podemos utilizar colores en los trabajos escolares.
¿Qué hacemos?
En esta sesión vamos a trazar varias rectas para encontrar las soluciones a los sistemas de ecuaciones lineales 2 por 2. Así que alumnas y alumnos, les recomendamos que tengan cerca de ustedes 2 colores distintos, uno para cada recta que se trazará.
¿Por qué vamos a trazar 2 rectas en un sistema de 2 ecuaciones con 2 incógnitas?
Vamos a trazar 2 rectas porque representaremos cada ecuación del sistema con una recta en el plano cartesiano.
¿Cómo podemos encontrar la solución de un sistema de 2 por 2 por el método gráfico?
¿Qué le parece si nos propone un sistema de ecuaciones y entre todos lo resolveremos?
Comencemos con un sistema que por sus características puede ser considerado sencillo de resolver y gradualmente aumentaremos la dificultad de ellos.
La primera ecuación del sistema es “y” más “x” es igual a 13 y la segunda, “y” más 6 “x” igual a 38.
Podemos resolver el sistema por diferentes caminos y diferentes métodos, pero, como les mencionamos anteriormente, en esta ocasión utilizaremos el método gráfico y el camino que nosotros les proponemos, es el siguiente:
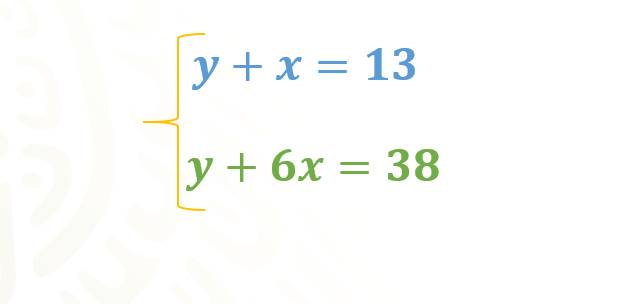
En ambas ecuaciones despejamos a “y”, es decir, la dejamos sola en un lado de la ecuación, haciendo uso de las propiedades de la igualdad.
Esto lo hacemos para que tengamos expresiones equivalentes a esas ecuaciones, pero de manera que las podamos observar como una relación donde el valor “y” está en función del valor de “x”.
Para la primera ecuación, primero, sustraemos “x” en ambos miembros de la igualdad, por lo que la ecuación ahora es “y” más “x”, menos “x”, igual a 13 menos “x”.
Reducimos los términos semejantes en el primer miembro de la ecuación, con lo que las “x” se eliminan entre sí dado que su suma es cero.
Con lo anterior, obtenemos “y” igual a 13 menos “x”.
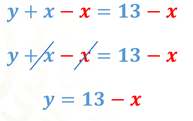
De la misma manera, despejamos “y” en la segunda ecuación.
Haciendo uso de las propiedades de la igualdad, sustraemos 6 “x” en ambos miembros de la igualdad, por lo que tenemos “y” más 6 “x”, menos 6 “x” igual a 38 menos 6 “x”.
Al reducir los términos semejantes en el primer miembro de la igualdad, se eliminan entre sí 6 “x” dado que su resultado es cero.
Con ello ya hemos despejado a “y”, como “y” igual a 38 menos 6 “x”.
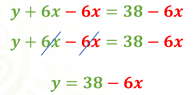
Ahora, podemos hacer uso de una tabla para organizar los valores de las coordenadas que vamos a calcular. La tabla permitirá diferenciar visualmente las coordenadas que corresponden a cada recta.
Puedes elaborar su tabla como gustes, te sugerimos el siguiente orden, observa la tabla.

En la primera columna colocaremos los valores de “x”.
En la segunda columna las operaciones que se generan al sustituir el valor de “x” en el despeje de “y” en la primera ecuación.
En la tercera columna las operaciones que se generan al sustituir el valor de “x” en el despeje de “y” para la segunda ecuación.
En la cuarta columna las coordenadas que se forman con el valor de “x” y el valor calculado de “y”, para la recta de la primera ecuación.
En la quinta columna las coordenadas que se forman con el valor de “x” y el valor calculado de “y”, para la recta de la segunda ecuación.
Pueden asignar los valores que ustedes gusten para “x”, es muy común que se asignen valores positivos, negativos y el cero para “x”, con la finalidad de observar el comportamiento de las rectas para valores dados. Nosotros asignamos valores enteros desde 3 negativo a 3 positivo.
| Primera ecuación | Segunda ecuación | |||
Sustituiremos los valores de “x” en el primer despeje, para encontrar el valor de “y” en cada caso de esas sustituciones.
Para “x” igual a 3 negativo, sustituimos y obtenemos “y” igual a 13 menos 3 negativo. Al resolver las operaciones el resultado es 16.
Para “x” igual a 2 negativo, tenemos “y” igual a 13 menos 2 negativo y al resolver las operaciones el resultado es 15.
Para “x” igual a uno negativo, la sustitución queda como “y” igual a 13 menos uno negativo de donde se obtiene que “y” es igual a 14.
| Primera ecuación | Segunda ecuación | |||
Para “x” igual a cero, “y” es igual a 13 menos cero lo que hace que “y” es igual a 13.
Para “x” igual a uno, al sustituir tenemos que “y” igual a 13 menos uno y al resolver las operaciones el resultado es 12.
Para “x” igual a 2, “y” es igual a 13 menos 2 con lo que se obtiene que “y” es igual a 11.
Por último, para “x” igual a 3, sustituimos con lo que tenemos que “y” es igual a 13 menos 3, por lo que “y” es igual a 10.
De la misma manera que en el paso anterior, sustituiremos los valores de “x” en el despeje de “y” de la segunda ecuación, para obtener el valor de “y” que corresponde a cada valor propuesto de “x”.
Iniciemos entonces, con el primero valor de “x”. Para “x” igual a 3 negativo, “y” es igual a 38 menos, 6 por 3 negativo, lo que hace “y” igual a 38 más 18, de donde se obtiene “y” igual a 56.
Para “x” igual a 2 negativo, “y” igual a 38 menos, 6 por 2 negativo, lo que hace “y” igual a 38 más 12, de donde se obtiene “y” igual a 50.
Para “x” igual a 1 negativo, “y” igual a 38 menos, 6 por 1 negativo, lo que hace “y” igual a 38 más 6, de donde se obtiene “y” igual a 44.
Para “x” igual a cero, tenemos que “y” igual a 38 menos 6 por cero, entonces “y” es igual a 38.
En el caso de “x” igual a uno, se tiene “y” igual a 38 menos, 6 por uno, con lo que se tiene “y” igual a 38 menos 6, entonces “y” es igual a 32.
Para “x” igual a 2, “y” es igual a 38 menos, 6 por 2; luego, “y” es igual a 38 menos 12, y al resolver la operación obtenemos que “y” es igual a 26.
Finalmente, para “x” igual a 3, tenemos “y” igual a 38 menos, 6 por 3, de donde se tiene “y” igual a 38 menos 18 por lo que “y” es igual a 20.
| Primera ecuación | Segunda ecuación | |||
Ya que hemos calculado los valores de “y”, formaremos con los valores de “x” y de “y” las coordenadas de cada uno de los puntos que corresponden a cada ecuación, ya que por dichos puntos pasarán las rectas, que son sus gráficas.
Los puntos de la primera recta, que corresponde a la ecuación “y” más “x” igual a 13, son los siguientes:
3 negativo coma 16.
2 negativo coma 15.
1 negativo coma 14.
Cero coma 13.
Uno coma 12.
2 coma 11.
3 coma 10.
| Primera ecuación | Segunda ecuación | |||
Los puntos de la segunda recta, que corresponde a la ecuación “y” más 6 “x” igual a 38, son los siguientes:
3 negativo coma 56.
2 negativo coma 50.
1 negativo coma 44.
Cero coma 38.
Uno coma 32.
2 coma 26.
3 coma 20.
| Primera ecuación | Segunda ecuación | |||
¿Qué piensan que debemos hacer a continuación?
Debemos ubicar estos puntos en un plano cartesiano para trazar las rectas que corresponden al sistema que queremos resolver.
Para que nosotros no confundamos los puntos de cada recta, ubicaremos las coordenadas de la primera recta y posteriormente, las de la segunda.
La primera coordenada es 3 negativo coma 16, por lo que nos desplazamos 3 lugares hacia la izquierda sobre el eje de las “x” o de las abscisas a partir del origen. Posteriormente, desde ahí nos desplazamos 16 lugares hacia arriba paralelamente al eje de las “y” o de las ordenadas. Ésa será la coordenada 3 negativo, coma 16.
La segunda coordenada es 2 negativo coma 15, por lo que nos desplazamos 2 lugares hacia la izquierda sobre el eje de las “x” o de las abscisas a partir del origen. Luego, y desde ese lugar, nos desplazamos 15 lugares hacia arriba paralelamente al eje de las “y” o de las ordenadas. Ésa será la coordenada 2 negativo, coma 15.
La tercera coordenada es uno negativo coma 14, por lo que nos desplazamos un lugar hacia la izquierda sobre el eje de las “x” o el eje horizontal a partir del origen. Desde ahí, nos desplazamos 14 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada uno negativo, coma 14.
La cuarta coordenada es cero coma 13, por lo que no nos desplazamos sobre el eje de las “x” o el eje horizontal. Luego partimos del origen, desde ese lugar, nos desplazamos 13 lugares hacia arriba sobre el eje de las “y”. Ésa será la coordenada cero, coma 13.
Para la quinta coordenada, que es 1 coma 12, nos desplazamos un lugar hacia la derecha sobre el eje de las “x” a partir del origen. Ahora, desde ahí, nos desplazamos 12 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 1, coma 12.
La sexta coordenada es 2 coma 11, por lo que nos desplazamos 2 lugares hacia la derecha sobre el eje de las “x” a partir del origen. Posteriormente, a partir de ahí, nos desplazamos 11 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 2, coma 11.
Finalmente, para la séptima coordenada que calculamos para la primera ecuación, que es 3 coma 10, nos desplazamos 3 lugares hacia la derecha sobre el eje de las “x” a partir del origen. Luego, desde ese lugar, nos desplazamos 10 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 3, coma 10.
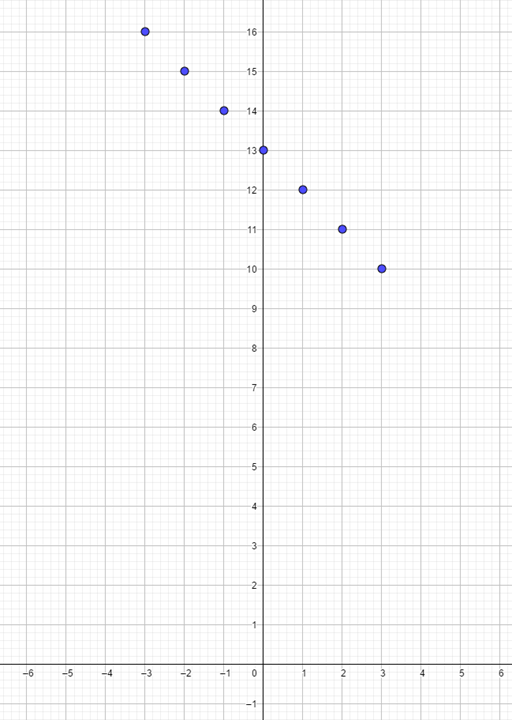
Una vez ubicados los puntos trazaremos una recta que pase por todos ellos. Con ello simbolizaremos a la recta que pasa por todas las coordenadas que colocamos y que representa a la primera ecuación.
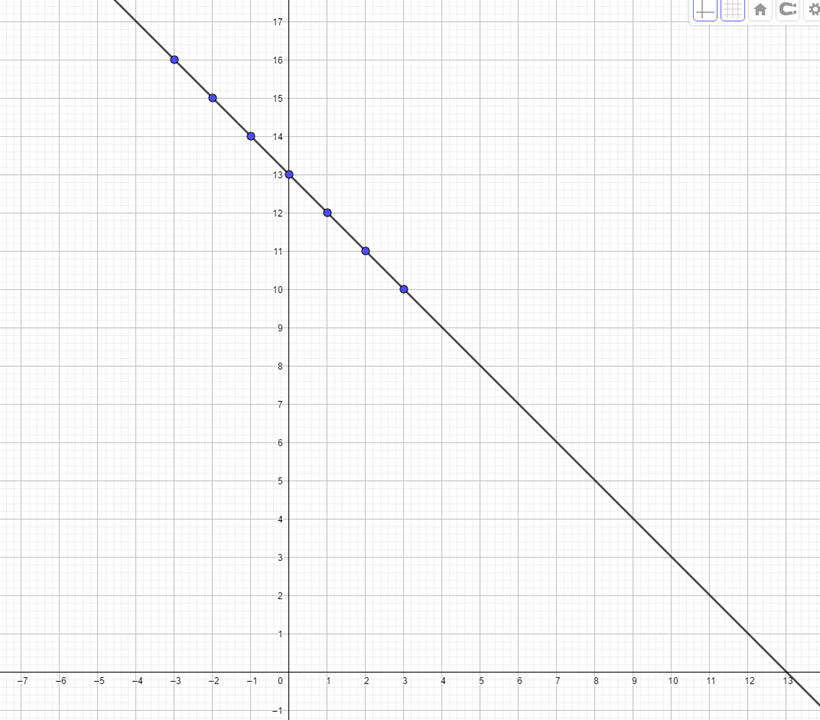
Ya que hemos ubicado las coordenadas de la primera recta y trazado su representación gráfica, colocaremos de la misma manera las coordenadas de la segunda ecuación.
La primera coordenada es 3 negativo coma 56, por lo que nos desplazamos 3 lugares hacia la izquierda del origen sobre el eje de las “x”. Desde ese lugar, nos desplazamos 56 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 3 negativo, coma 56.
La segunda coordenada es 2 negativo coma 50, por lo que nos desplazamos 2 lugares hacia la izquierda del origen sobre el eje de las “x” y posteriormente, a partir de ahí, nos desplazamos 50 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 2 negativo, coma 50.
La tercera coordenada es 1 negativo coma 44, por lo que nos desplazamos un lugar hacia la izquierda del origen sobre el eje de las “x”. Luego, desde ese lugar, nos desplazamos 44 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 1 negativo, coma 44.
La cuarta coordenada es cero coma 38, por lo que no nos desplazamos sobre el eje de las “x” y sí lo hacemos sobre el eje de las “y”, desde el origen, 38 lugares hacia arriba. Esa será la coordenada cero, coma 38.
Para la quinta coordenada que es 1 coma 32, nos desplazamos un lugar hacia la derecha del origen sobre el eje de las “x”. Posteriormente, desde ahí, nos desplazamos 32 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 1, coma 32.
Para el caso de la sexta coordenada que es 2 coma 26, nos desplazamos 2 lugares hacia la derecha del origen sobre el eje de las “x”. Luego, desde ese lugar, nos desplazamos 26 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 2, coma 26.
La séptima coordenada es 3 coma 20, por lo que nos desplazamos 3 lugares hacia la derecha del origen sobre el eje de las “x”. Posteriormente, a partir de ahí, nos desplazamos 20 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 3, coma 20.
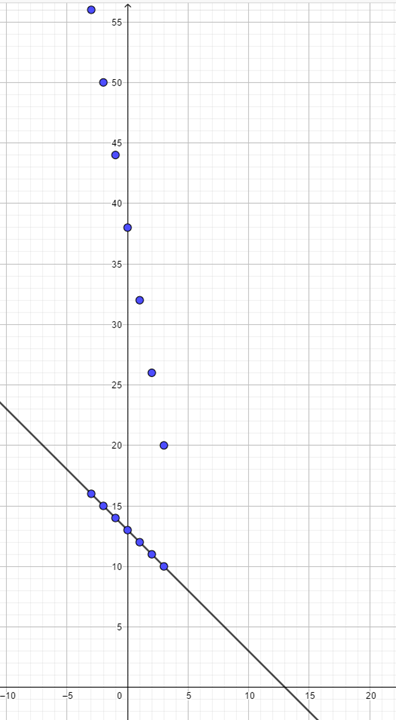
¿Qué hacemos para continuar?
Trazamos una recta que pase por todos los puntos que acabamos de localizar, prolongando sus extremos.
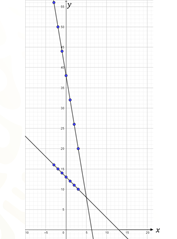
Observa el plano que aparece en sus pantallas, donde ya fueron trazadas las 2 rectas que genera el sistema de ecuaciones de 2 por 2 que estamos resolviendo.
¿En dónde podemos observar la solución al sistema? Es decir, el valor de “x” y el valor de “y”, que satisfacen las condiciones de las 2 ecuaciones al mismo tiempo.
Exacto, ya se dieron cuenta que la solución se encuentra en el punto donde las rectas se intersecan, es decir, el punto donde se cortan, esto es en la coordenada 5 coma 8.
Esto quiere decir que “x” es igual a 5 y que “y” es igual a 8.
Pero ¿cómo podemos estar seguros de que esos valores de las incógnitas son la solución del sistema de ecuaciones motivo de esta actividad?
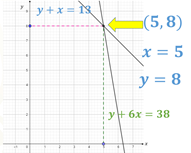
Esto lo podemos averiguar sustituyendo los valores obtenidos para “x” y para “y” en las ecuaciones iniciales y observar si se cumple la igualdad.
Vamos a hacerlo.

Si sustituimos en la primera ecuación que es “y” más “x” igual a 13 obtenemos 8 más 5 igual a 13. Al sumar comprobamos la igualdad, 13 igual a 13.
En la segunda ecuación, “y” más 6 “x” igual a 38, sustituimos y obtenemos 8 más, 6 por 5 igual a 38. Al realizar la multiplicación resulta 8 más 30 igual a 38 y, al sumar obtenemos la igualdad, 38 igual a 38.
De esta manera, al comprobar que los valores que obtuvimos, “x” igual a 5 y “y” igual a 8, hacen verdaderas las igualdades de ambas ecuaciones, podemos afirmar que son las soluciones del sistema formado por “y” más “x” igual a 13 y “y” más 6 “x” igual a 38.
Así es, maestro, ¿qué le parece si resolvemos, junto con las alumnas y los alumnos, un problema?
Resolvamos el siguiente problema.
El doble de un número más el quíntuple de otro es igual a 19 negativo. Se sabe que el triple del primero menos el séxtuple del segundo es 12. ¿Cuáles son esos números?
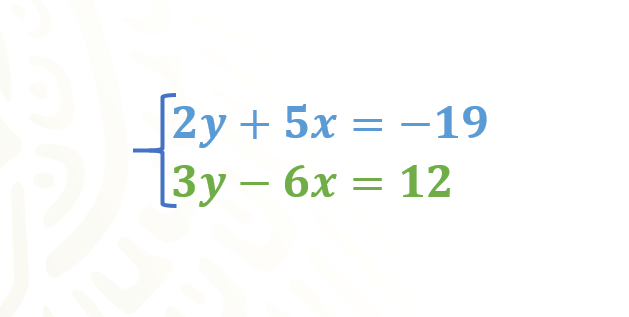
Para la primera ecuación: 2 “y” más 5 “x” igual a 19 negativo y para la segunda ecuación 3 “y” menos 6 “x” igual a 12.
Resolver este sistema involucrará pasos adicionales comparado con el que respondimos anteriormente, ya que como seguramente ya se dieron cuenta, la “y” no está del todo sola. En ambos casos tiene un coeficiente distinto de uno.
Sin embargo, de manera general, seguiremos los mismos pasos que en el caso anterior.
Comencemos despejando la “y” en ambas ecuaciones.
Para la primera ecuación restamos 5 “x” en ambos lados de la ecuación. Al reducir términos semejantes resulta 2 “y” igual a 19 negativo menos 5 “x”. Como la “y” aún no está sola dividiremos los dos miembros de la igualdad entre 2, este es el paso adicional que no hicimos en el sistema anterior.
Al dividir entre 2, ya tenemos despejada a la “y”, como “y” igual a 19 negativo menos 5 “x”, entre 2.
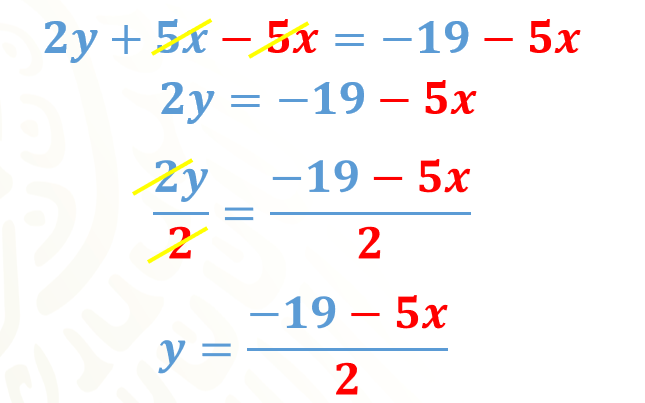
Una manera de despejar “y” en la segunda ecuación, es sumar 6 “x” en ambos miembros de la igualdad, con ello tenemos 3 “y” es igual a 12 más 6 “x”.
Como la “y” aún no está despejada, dividimos entre 3 a ambos miembros de la igualdad, con lo que obtenemos “y” es igual a 12 más 6 “x”, entre 3.
¿Qué hacemos para continuar?
Podemos continuar dando valores para “x” y determinar el que le corresponda para “y” en ambos despejes realizados anteriormente.
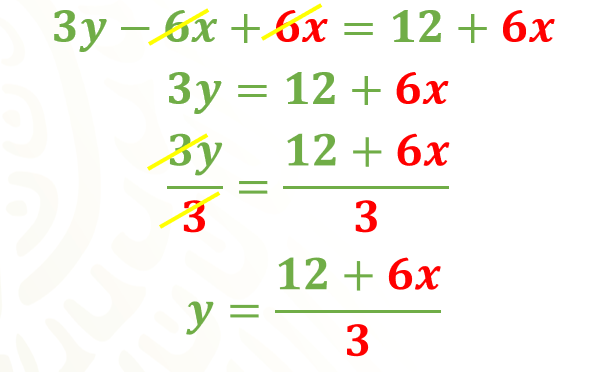
Para organizar los datos que nos llevarán a trazar las gráficas, usaremos una tabla similar a la del sistema anterior, pero ahora no usaremos tantos valores. Así que usaremos 3 valores, un valor positivo, uno negativo y el cero.
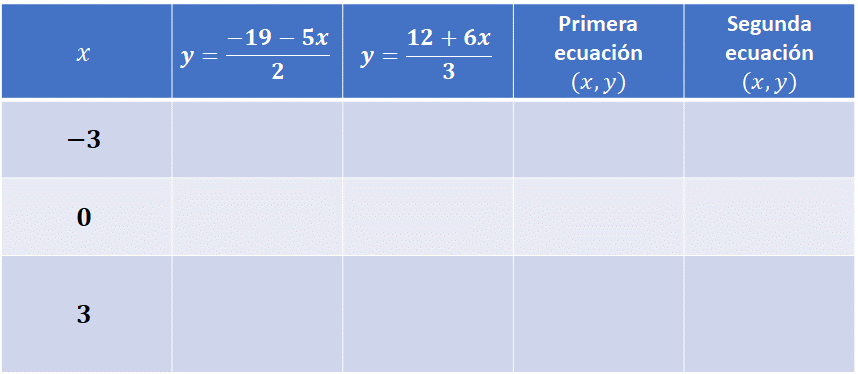
De la misma manera que en el procedimiento anterior, sustituimos los valores de “x” en el primer despeje de “y”.
Para “x” igual a 3 negativo, sustituimos y obtenemos “y” igual a 19 negativo, menos, 5 por 3 negativo, entre 2, y al resolver las operaciones obtenemos 2 negativo.
Ahora, para “x” igual a cero, sustituimos y obtenemos “y” igual a 19 negativo, menos, cinco por cero, entre 2, lo que da como resultado 9 punto 5 negativo.
Por último, para “x” igual a 3, al sustituir tenemos “y” igual a 19 negativo, menos 5 por 3, entre 2, y al resolver las operaciones obtenemos que “y” es igual a 17 negativo.
| Primera ecuación | Segunda ecuación | |||
Ahora, sustituimos los valores de “x” en el despeje de “y” de la segunda ecuación:
Para “x” igual a 3 negativo, tenemos “y” igual a 12 más, 6 por 3 negativo, entre 3 y al resolver las operaciones obtenemos “y” igual a 2 negativo.
| Primera ecuación | Segunda ecuación | |||
En el caso de “x” igual a cero, “y” igual a 12 más, 6 por cero, entre 3 y al resolver las operaciones determinamos que “y” es igual a 4.
Por último, para “x” igual a 3, “y” es igual a 12 más, 6 por 3, entre 3, de donde obtenemos “y” igual a 10.
Con lo anterior obtenemos las coordenadas asignadas a algunos puntos de ambas rectas.
¿Qué notas al comparar los puntos de ambas rectas?
A partir de los datos de la tabla, ¿podemos saber si habrá un punto en común para ambas rectas?
Vayamos a la representación de las gráficas del sistema para resolverlo.
| Primera ecuación | Segunda ecuación | |||
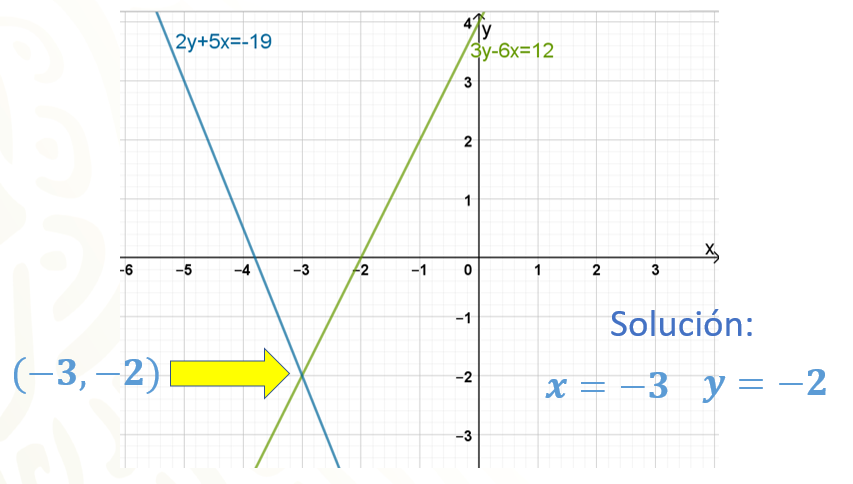
Observa las rectas que representan el sistema. ¿En dónde se observa la solución a este sistema?
Seguramente ya identificaste que la coordenada en donde se cortan las rectas es la 3 negativo coma 2 negativo, y esto significa que la solución del sistema es “x” igual a 3 negativo y “y” igual a 2 negativo.
El reto de hoy:
Como reto te corresponde realizar la comprobación de estos valores.
Con esto hemos llegado al final de esta sesión. Recuerden que este es un material de apoyo y que, para complementar lo estudiado, pueden consultar otras fuentes, como su libro de texto de matemáticas de segundo grado.
Si quieres volver a ver los programas de Aprende en casa transmitidos en semanas previas, los puedes encontrar en la página: youtube.com/aprendeencasa
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas