Cociente de potencias de la misma base II
Cociente de potencias de la misma base II
Aprendizaje esperado: resuelve problemas de potencias con exponente entero y aproxima raíces cuadradas.
Énfasis: dar sentido y significado a los procedimientos para calcular cocientes de potencias enteras de la misma base.
¿Qué vamos a aprender?
Resolverás situaciones para dar sentido y significado a los procedimientos para calcular cocientes de potencias enteras de la misma base, partiendo del concepto de potencia y de la multiplicación de potencias.
¿Qué hacemos?
Para iniciar resuelve la siguiente situación.
Una empresa que fabrica recipientes los elabora de tres tamaños diferentes, todos de forma cúbica. El recipiente “A” mide 3 centímetros de arista, el recipiente “B” mide 9 centímetros de arista y el recipiente “C”, 27 centímetros de arista.

¿Ya tienes tus respuestas? Es momento de iniciar.
¿Recuerdas cómo calcular el volumen de un cubo?
Como sabes, la fórmula para calcular el volumen de un cubo se obtiene multiplicando tres veces por sí mismo el valor de su arista, es decir, arista por arista por arista, o arista al cubo.
Entonces aplica esta fórmula para calcular el volumen de los recipientes.
En cuanto al recipiente “A”.
Volumen es igual a 3 centímetros por 3 centímetros, por 3 centímetros, que es igual a 3 al cubo centímetros cúbicos que son 27 centímetros cúbicos.
Con respecto al recipiente “B”.
Volumen es igual a 9 centímetros por 9 centímetros, por 9 centímetros, que es igual a 9 al cubo centímetros cúbicos, que son 729 centímetros cúbicos.
Para el recipiente “C”.
Volumen es igual a 27 centímetros por 27 centímetros, por 27 centímetros, que es igual a 27 al cubo centímetros cúbicos, que son 19 683 centímetros cúbicos.

Ahora expresa el volumen de los tres recipientes como potencias, pero usa la misma base.
Para el recipiente “A”, la medida de la arista es 3 centímetros y el volumen es igual a 3 centímetros por 3 centímetros, por 3 centímetros, que es igual a 3 al cubo centímetros cúbicos que son 27 centímetros cúbicos.
En el recipiente “B”, su arista mide 9 centímetros que se pueden expresar como 3 por 3 centímetros, lo que es igual a 3 al cuadrado centímetros. Como el volumen es igual a arista por arista, por arista, entonces, volumen es igual a 3 al cuadrado centímetros por 3 al cuadrado centímetros, por 3 al cuadrado centímetros, que es igual a 3 a la 6 centímetros cúbicos.
Para el recipiente “C”, sabes que la arista mide 27 centímetros, que expresada como potencia de 3 es 3 al cubo centímetros, entonces para calcular su volumen se multiplica 3 al cubo centímetros por 3 al cubo centímetros, por 3 al cubo centímetros, que resulta 3 a la 9 centímetros cúbicos.

Reflexiona, ¿cómo se puede saber las veces que el volumen de un recipiente es el volumen de otro?
Esta comparación se hace por medio de una razón o de un cociente.
Para saber cuántas veces el volumen del recipiente “C” es el volumen del recipiente “B”, se hace un cociente de los volúmenes.
Calcula el cociente para comparar los volúmenes de los recipientes “C” y “B”. Considera que las medidas de los volúmenes están dadas en centímetros cúbicos. De esa manera se tiene que el volumen del recipiente “C” entre el volumen del recipiente “B” es igual a 19 683 entre 729 que es igual a 27, lo que significa que el volumen del recipiente “C” es 27 veces el volumen del recipiente B.
Por otro lado, si se expresa el volumen de los recipientes como potencias de 3, se tiene que el volumen del recipiente “C” entre el volumen del recipiente “B” es igual a la potencia 3 a la 9 entre la potencia 3 a la 6 que es igual a 27.
Pero como 27 es 3 al cubo se tiene que la potencia 3 a la 9 entre la potencia 3 a la 6 es igual a 3 al cubo.

¿Qué piensas que se hace con los exponentes al dividir dos potencias de la misma base?
¿Cuántas veces el volumen del recipiente “C” es el volumen del recipiente “A”?
El cociente del volumen “C” entre el volumen “A” es igual a la potencia 3 a nueve entre la potencia 3 al cubo, que es igual a 19 683 entre 27, lo que resulta en 729. Esto significa que el volumen del recipiente “C” es 729 veces el volumen del recipiente “A”.
Por otro lado, si se expresa el volumen de los recipientes como potencias de 3, se tiene que el volumen del recipiente “C” entre el volumen del recipiente “B” es igual a la potencia 3 a la 9 entre la potencia 3 al cubo que es igual a 729.
Pero como 729 es 3 elevado a la potencia 6, entonces se tiene que 3 a la potencia 9 entre 3 a la potencia 3 es igual a 3 a la potencia 6.

¿Ya encontraste una forma de calcular el cociente de potencias de la misma base?
¿Qué sucede con el procedimiento de la división de potencias?
¿Cuál es el resultado y cómo se obtiene?
Como se vio en uno de los resultados de la actividad anterior, el cociente de la potencia 3 a la 9 entre la potencia 3 a la 6, es igual a la potencia 3 a la 3, lo cual pudiera pensarse que se obtiene de mantener la base de las potencias que se dividen con el exponente que resulta de restar los exponentes del dividiendo menos el del divisor.
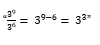
¿Pensaste en esta forma de calcular el cociente?
Pero ¿cómo puedes calcular este resultado de otra manera?
Sabes que la potencia es una forma de representar una multiplicación de factores iguales, donde la base es el factor, es decir el número que se multiplica y el exponente es el número de veces que la base se escribe como factor, por lo que observa nuevamente la división de la potencia 3 a la 9 entre la potencia 3 a la 6.
Si las potencias de la división se escriben como multiplicación, se tiene 3 por 3, por 3, por 3, por 3, por 3, por 3, por 3, por 3, entre 3 por 3, por 3, por 3, por 3, por 3.
A continuación, podrás separar factores del dividiendo y del divisor, y hacerlos corresponder uno a uno. De esta manera, se tiene 3 entre 3, por 3 entre 3, por 3 entre 3, por 3 entre 3, por 3 entre 3, por 3 entre 3, por 3, por 3, por 3.
Al simplificar cada división de 3 entre 3 se obtiene 1. Por eso el resultado es 1 por 1, por 1, por 1, por 1, por 1, por 3, por 3, por 3.
Como 1 es el elemento neutro multiplicativo, la multiplicación anterior es equivalente a 3 por 3 por 3.
Si la multiplicación 3 por 3, por 3, se expresa como potencia resulta 3 al cubo.
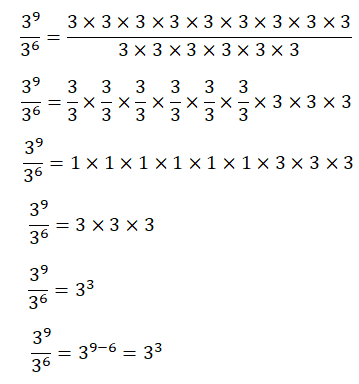
Por lo tanto, de esta manera también verás que el resultado podría obtenerse restando los exponentes del dividendo menos el del divisor y manteniendo la misma base.
¿Piensas que esta manera funciona siempre así?
Seguramente en estudios superiores de matemáticas tendrás la oportunidad de justificar esta manera de calcular el cociente de potencias de la misma base.
Piensa, ¿cómo puedes enunciar este procedimiento o regla para dividir potencias de la misma base?
Se espera que ya tengas tu respuesta. Compárala con la siguiente.
Cuando divides potencias de la misma base el resultado se expresa en la misma base y con el exponente resultado de restar los exponentes de la potencia del dividendo menos el exponente de la potencia del divisor.
La propiedad o regla anterior se expresa de forma generalizada a través de la expresión “a” a la “m” entre “a” a la “n” es igual a “a” a la “m” menos “n”, con “a” diferente de cero, y “m”, “n” son enteros positivos.
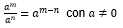
Aplica la regla en los siguientes ejemplos.
Primero calcula el cociente de “m” elevado a la 7 entre “n” elevado al exponente 6. Luego, el cociente de la potencia 20 a la 72 entre la cuarentaicincoava potencia de 20.

Para el ejemplo 1, si aplicas la regla para calcular el cociente de potencias con la misma base se tiene que el cociente de “m” a la 7 entre “m” a la 6 es igual a la potencia de base “m” y exponente es la diferencia de 7 menos 6, de donde se obtiene “m” a la uno. ¿Recuerdas que se puede omitir la escritura del exponente 1? Por ello, este resultado podría expresarse como “m”.
Ahora desarrolla el cociente anotando las potencias del numerador y del denominador como multiplicaciones. De esta manera se tiene que “m” a la 7 entre “m” a la 6 es igual a “m” por “m”, por “m”, por “m”, por “m”, por “m”, por “m”, entre “m” por “m”, por “m”, por “m”, por “m”, por “m”.
Si expresas como fracción los factores que se pueden simplificar del dividendo con los del divisor, tienes seis factores que son divisiones de “m” entre “m”. Al multiplicar estas fracciones se obtiene “m” a la 6 entre “m” a la 6 por “m”.
De la fracción “m” a la potencia 6 entre “m” a la potencia 6 se obtiene 1, que se multiplica por el factor que no se simplificó, en este caso es por “m”.
Entonces el resultado “m” a la 7 entre “m” a la 6 es igual a “m”. Lo mismo que se obtuvo con el procedimiento anterior.

Para el ejemplo 2 se debe calcular el cociente de las potencias de la misma base, 20 a la 72 entre 20 a la 45.
Si aplicas la propiedad o generalización de la regla que se está trabajando, se tiene que el cociente de 20 a la 72 entre 20 elevado a la 45 es igual a 20 elevado al exponente que resulte de restar 72 menos 45, esto es, 20 elevado a la 27.
Por otro lado, también es posible expresar la potencia del dividendo 20 elevado a la 72 como el producto de las potencias 20 elevado a la 45 por 20 elevado a la 27, ya que 45 y 27 suman 72, y esto entre la potencia 20 elevado a la 45.
Posteriormente se puede realizar una descomposición de la operación del segundo miembro de la igualdad y se tiene que el cociente 20 elevado a la 72 entre 20 elevado a la 45 es igual al cociente 20 elevado a la 45 entre 20 elevado a la 45, por 20 elevado a la 27.
Al dividir 20 elevado al exponente 45 entre 20 elevado al exponente 45 se obtiene 1. Por lo que 20 elevado a la 72 entre 20 elevado a la 45 es igual 1 por la potencia 20 elevado a la 27.
Por la propiedad del elemento neutro multiplicativo se concluye que 20 elevado a la 72 entre 20 elevado a la 45 es igual a 20 elevado a la 27. Que es el mismo resultado con la aplicación de la regla que se ha trabajado.

Ahora es momento de poner en práctica lo aprendido. Resuelve la siguiente actividad. Anota tus resultados en tu cuaderno. Realiza tus cálculos de manera mental.
Primero resuelve el cociente de 9 a la 18 entre 9 a la 12.
Luego, escribe cuál es el cociente de la vigésimo sexta potencia de equis, entre “x” a la cuarta.
A continuación ¿cuál es el cociente de 2 quintos elevado a la 7 entre 2 quintos elevado al cubo?
Finalmente determina el cociente de 0 punto 12 elevado al exponente 15, entre 0 punto 12 elevado al exponente 10.
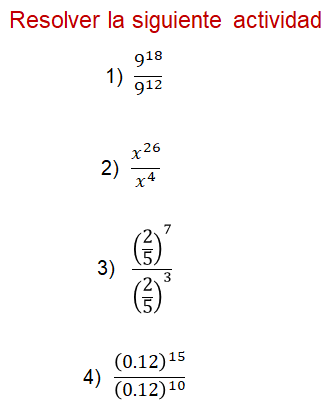
¿Ya tienes los resultados?
Comienza a dar solución a la actividad; no olvides registrar tus dudas y lo que te resulte interesante de la sesión. Así como el registrar tus respuestas a los planteamientos propuestos.
Inciso 1. El cociente de 9 elevado a la 18 entre 9 elevado a la 12 es igual a 9 elevado a la 18 menos 12, igual a la potencia 9 a la 6.
En el inciso 2, el cociente de “x” elevado a la 26 entre “x” elevado a la 4, es igual a “x” elevado a la 26 menos 4, igual a “x” a la 22.
Para la división correspondiente a potencias con base fraccionaria, se tiene que el cociente de 2 quintos elevados al exponente 7 entre 2 quintos elevados al cubo, es igual a 2 quintos elevados a 7 menos 3, igual a 2 quintos elevados a la 4.
En el último inciso, la propiedad se presenta para números decimales. Aquí, se calcula el cociente de cero punto 12 elevado a la 15 entre cero punto 12 elevado a la 10 que es igual a cero punto 12 elevado a la 15 menos 10, igual a cero punto 12 elevado a la 5.
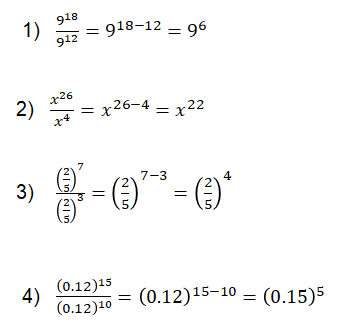
¿Son los mismos resultados que tú obtuviste?
Ahora, se te propone resolver la siguiente situación.
Se te invita a dar respuesta a la situación. Piensa por tres segundos. ¿Cómo la resolviste?
Ahora, se compararán tus respuestas con las que presentarán a continuación.
Primero, ¿qué datos conoces?
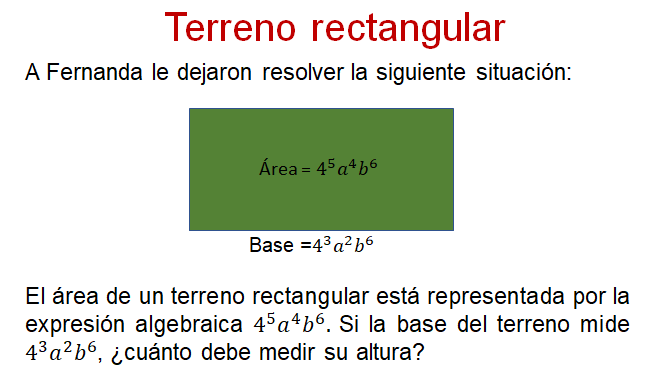
Sabes que el área del terreno rectangular es la expresión 4 a la 5, “a” cuarta, “b” sexta. Y que la medida de la base es 4 al cubo, “a” cuadrada, “b” sexta.
También sabes que el área de un rectángulo se calcula multiplicando la expresión de la base por la de la altura.
Como te das cuenta, se conocen dos de los tres valores que intervienen en la fórmula del área del rectángulo, por lo tanto, si se sustituyen esos valores en la fórmula, se tiene 4 a la 5, “a” cuarta, “b” sexta, es igual a 4 al cubo, “a” cuadrada “b” a la seis, por el valor desconocido de la altura.
Ahora divides ambos miembros de la igualdad entre 4 al cubo, “a” cuadrada, “b” a la 6, para despejar el valor de la altura.
Ahora simplifica del lado derecho, uno por el valor de la altura igual al valor de la altura.
Así obtienes que el valor de la altura es igual al cociente de 4 a la 5, “a” cuarta, “b” sexta entre a 4 al cubo, “a” cuadrada, “b” a la seis.
Para encontrar el resultado se aplica la propiedad o regla del cociente de potencias con la misma base.
Entonces la medida de la altura es igual a 4 a la 5 menos 3; “a” a la 4 menos 2; “b” a la potencia 6 menos 6.
De donde se obtiene 4 al cuadrado, “a” al cuadrado, “b” a la 0.
Recuerda que “b” elevada a la potencia 0 se obtiene de dividir “b” elevada a la potencia 6 entre sí misma, lo que en este caso resulta 1, siendo b diferente de cero.
Finalmente se obtiene como resultado 4 al cuadrado, “a” al cuadrado.

A continuación, se te invita a reflexionar acerca de la siguiente situación.
Da respuesta a la pregunta del problema, registra tu resultado y compáralo con lo que se te presenta.
Esta es una situación del Sol a la Tierra.

Al realizar la investigación, encontraron que la distancia que hay entre el Sol y la Tierra es de 1 punto cinco por 10 elevado a los 8 kilómetros y la velocidad que recorre la luz es de 300 000 kilómetros por segundo aproximadamente.
Con esta información ¿qué debes hacer para determinar el tiempo?
Sheila le dice a Aníbal que para calcular el tiempo sólo deben dividir la distancia del Sol a la Tierra entre la velocidad de la luz, ¿está en lo correcto?
Hay que comprobar los resultados.
En tu curso de Física, viste el tiempo que recorre un móvil, una distancia a una velocidad constante se calcula dividiendo la distancia entre la velocidad.
De esta manera, para dar respuesta al problema de Sheila y Aníbal, se divide la distancia que debe recorrer la luz del Sol a la Tierra, esto es, uno punto 5 por 10 elevado a la 8 kilómetros entre la velocidad de la luz que es de 300 000 kilómetros por segundo.
Luego, si se escribe la velocidad de la luz en notación científica, se tiene que el tiempo es igual a 1 punto 5 por 10 elevado a la 8 kilómetros entre 3 por 10 elevado a la 5 kilómetros por segundo.
Ahora una forma de resolver la división es separar los factores del dividiendo de manera que ahora se tiene que el tiempo es igual a 1 punto 5 entre 3 por el cociente de 10 elevado a la 8 kilómetros por segundo entre 10 elevado a la 5 kilómetros.
Al resolver las divisiones se obtiene que el tiempo es igual a cero punto 5 por 10 elevado a la 8 menos 5 segundos. Lo que es igual a cero punto 5 por 10 al cubo segundos. Como 10 a la 3 es 1 000, entonces el tiempo es igual a cero punto 5 por 1 000 segundos.
De lo anterior se determina que el tiempo que tarda la luz del Sol en llegar a la Tierra es de 500 segundos, lo equivalente a 8.33 minutos.
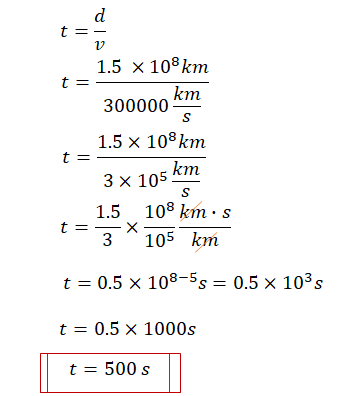
¿Cómo te fue en el resultado?
En esta sesión se ha dado sentido y significado a los procedimientos para calcular cocientes de potencias enteras de la misma base.
Has concluido la sesión del día de hoy.
El reto de hoy:
Indaga en donde más se puede utilizar la propiedad del cociente de potencias de la misma base. Además, se te invita a que resuelvas las actividades que se te indiquen en tu libro de texto que correspondan al aprendizaje trabajado en esta sesión.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas