Lectura y elaboración de gráficas de movimiento
Lectura y elaboración de gráficas de movimiento
Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: leer y elaborar gráficas formadas por secciones rectas y curvas que modelan situaciones de movimiento.
¿Qué vamos a aprender?
Prepara tu cuaderno de apuntes, lápiz y goma.
Anota lo que consideres importante para no perder detalle de la información. Esto te permitirá llevar un orden en las actividades y retomar los temas con mayor claridad.
En diversas ocasiones has resuelto y analizado problemas que involucran la construcción de una expresión algebraica lineal o cuadrática. Así como la construcción y lectura de sus representaciones gráficas para obtener información adicional de las situaciones que representan.
Aprenderás a leer y elaborar gráficas formadas por secciones rectas y curvas que modelan situaciones de movimiento.
La sesión está dividida en 3 momentos de aprendizaje:
- Primero, se identifica qué es una gráfica formada por secciones rectas y curvas.
- Después, se leen y se representan gráficas por secciones que modelan situaciones de movimiento.
- Al final, realizarás una actividad donde pongas en juego los conocimientos adquiridos.
¿Qué hacemos?
Un avión está en reposo antes de despegar, y poco a poco aumenta su velocidad hasta llegar a volar.
Estando en el aire mantiene una velocidad constante. Como éste, existen otros fenómenos relacionados con la variación del movimiento.
Pero ¿cómo se refleja este hecho en una gráfica?
Para determinarlo, primero observa el plano cartesiano.
Las representaciones gráficas provienen de relaciones que se representan en un plano cartesiano.
Un plano cartesiano se compone de dos rectas numéricas perpendiculares: una horizontal y otra vertical, que se cortan en un punto llamado origen o punto cero.

- El eje de las abscisas está dispuesto de manera horizontal, y se identifica con la letra “x”.
- El eje de las ordenadas está orientado verticalmente, representado con la letra “y”.
La interpretación de gráficas que modelan problemas o fenómenos reales, no necesariamente siguen un patrón definido o fórmula única. Esto da lugar a cierto tipo de gráficas que se elaboran y analizan por secciones.
Las gráficas por segmentos o “secciones” se llaman así porque su forma depende del segmento o sección en el que se encuentren.
Por ejemplo, la siguiente gráfica se compone de dos secciones: una corresponde a un segmento curvo y la otra a un segmento recto.
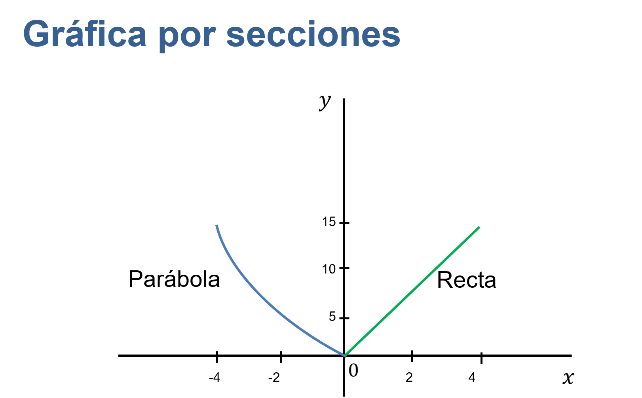
En el segundo cuadrante es un segmento de parábola, y en el primer cuadrante es un segmento de recta.
En el cero u origen se “juntan” las dos secciones de la gráfica, pues en ambos casos el valor de “y” es cero.
Para construir gráficas por secciones, se tienen los siguientes pasos:
Se determina el intervalo sobre el eje de las “x”, donde se define la sección. Es decir, se identifican los valores de inicio y término.
Después, se identifican los valores en el eje de las “y”.
Se repite el procedimiento tantas veces como regiones integren la gráfica.
Y el resultado final queda indicado en gráficas por secciones.
Para dejar aún más claro estos conceptos, resuelve la siguiente situación.
La gráfica corresponde al día que Ángel se dirigió a las canchas de basquetbol para su entrenamiento. Al llegar ahí, permaneció un tiempo esperando a su profesor, hasta que se acercó el señor encargado de la limpieza, quien le comentó que el entrenamiento de ese día se había suspendido. Y, por lo tanto, Ángel regresó a casa.
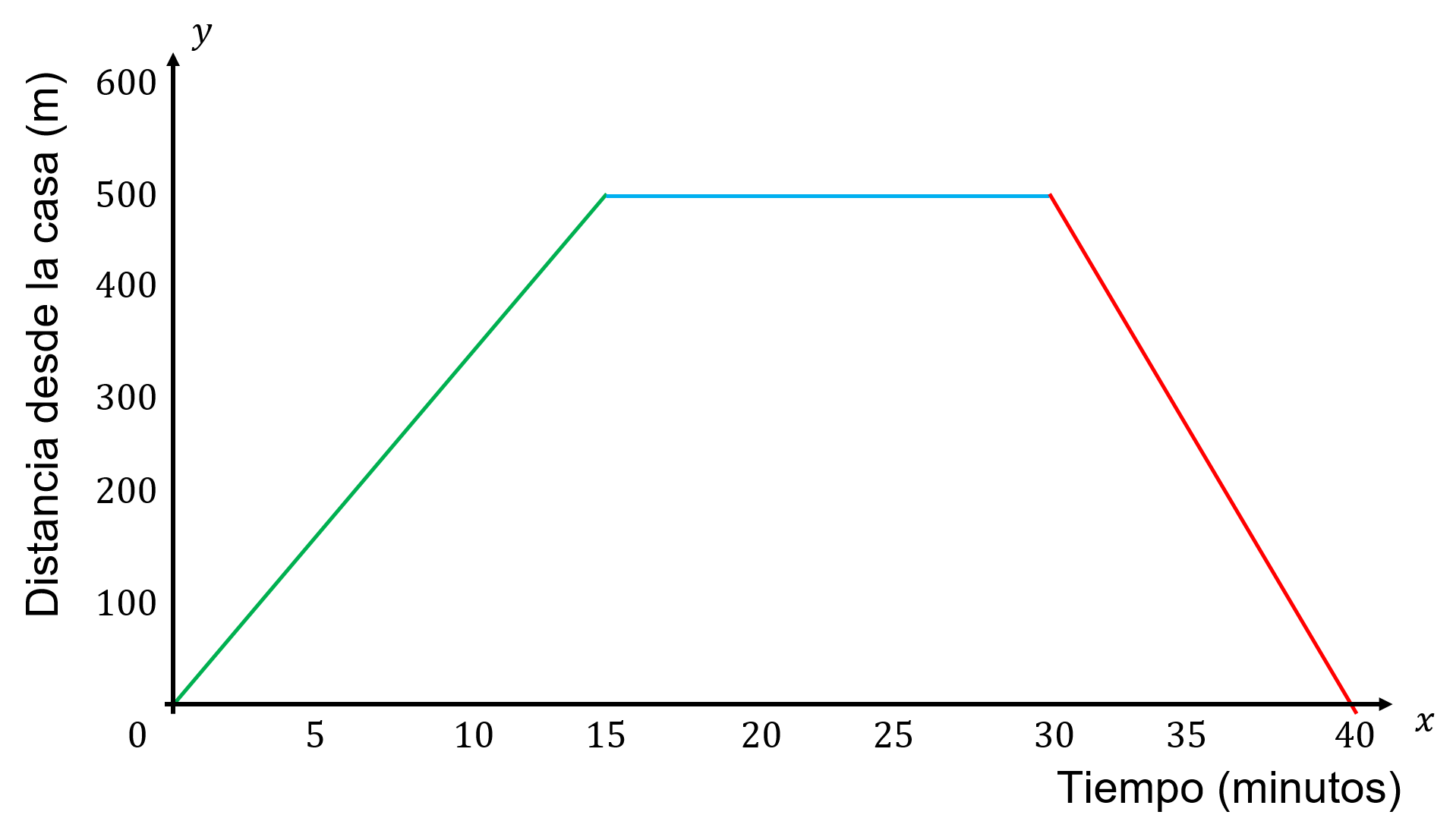
La gráfica que representa el traslado de la casa de Ángel a las canchas de basquetbol es una gráfica de segmentos de recta, donde se relaciona el tiempo y la distancia.
Para interpretar esos segmentos de recta, se contestan las siguientes preguntas:
¿Cuál es la distancia total que recorre Ángel?
Para responderlo, se observa el eje de las “x” donde se indica el tiempo en minutos.
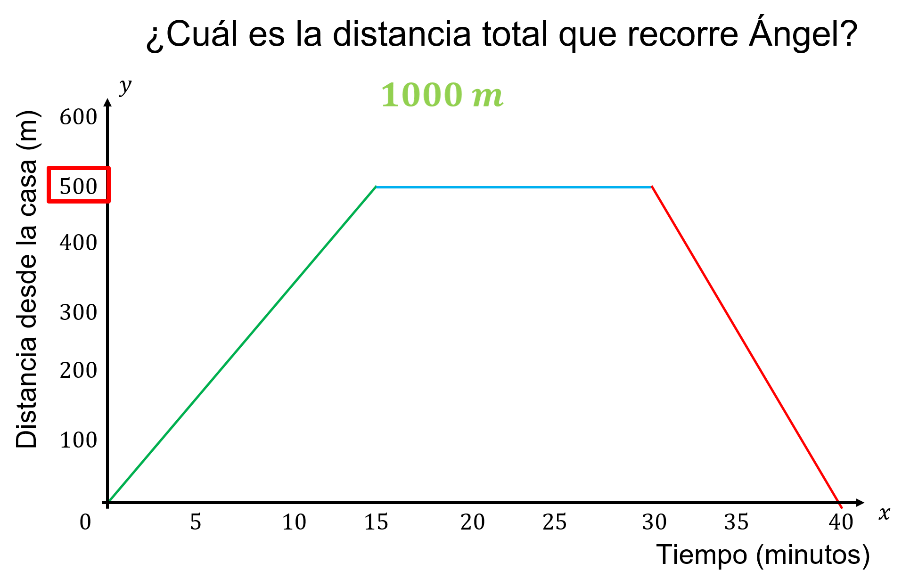
En el eje de las “y” se indica la distancia en metros.
Y para saber cuál es la distancia total recorrida por Ángel, se observa el eje de las “y”, y se suman las distancias de sus recorridos.
Ángel recorrió 500 metros de su casa a las canchas; ahí permaneció y al regresar a casa recorrió nuevamente 500 metros. La distancia total es de 1000 metros.
¿Cuánto tiempo hace de su casa a las canchas de basquetbol?
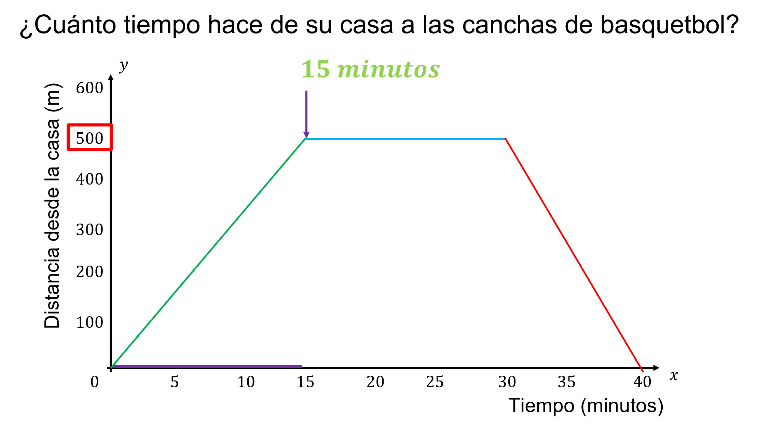
El eje de las “x” indica el tiempo transcurrido desde su salida de casa.
El tiempo que Ángel empleó para llegar a las canchas de basquetbol fue de 15 minutos, como se muestra en la gráfica.
¿Cuánto tiempo esperó Ángel hasta que se enteró de la suspensión del entrenamiento?
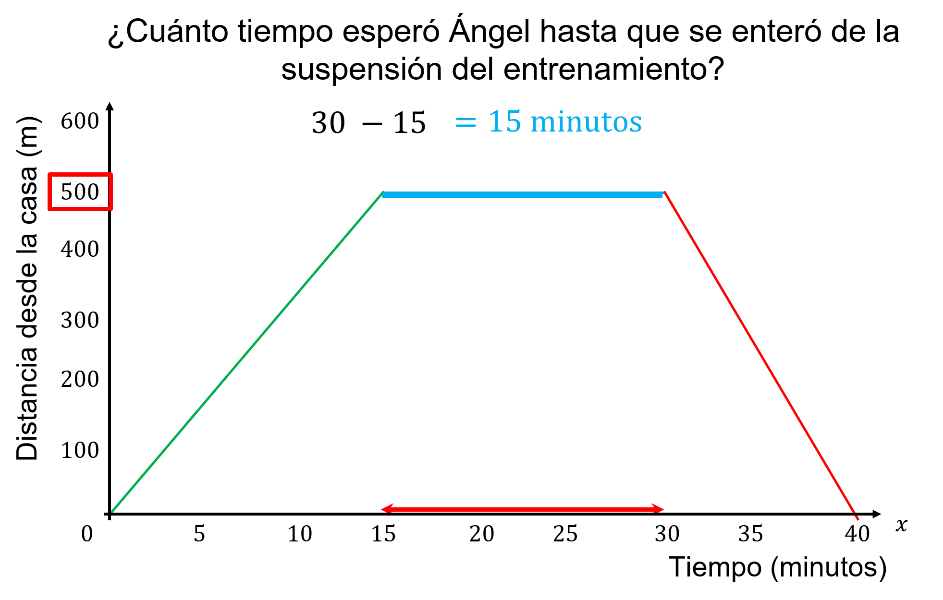
En la gráfica se observa la permanencia de Ángel del minuto 15 al minuto 30. Es decir, hay una línea recta indicando que no tuvo desplazamiento durante los minutos transcurridos.
Entonces, la diferencia de 30 menos 15 es igual a 15.
Y el tiempo de espera de Ángel fue de 15 minutos.
Si Ángel sale de su casa a las 3:40 de la tarde, ¿a qué hora llegó a las canchas de basquetbol?
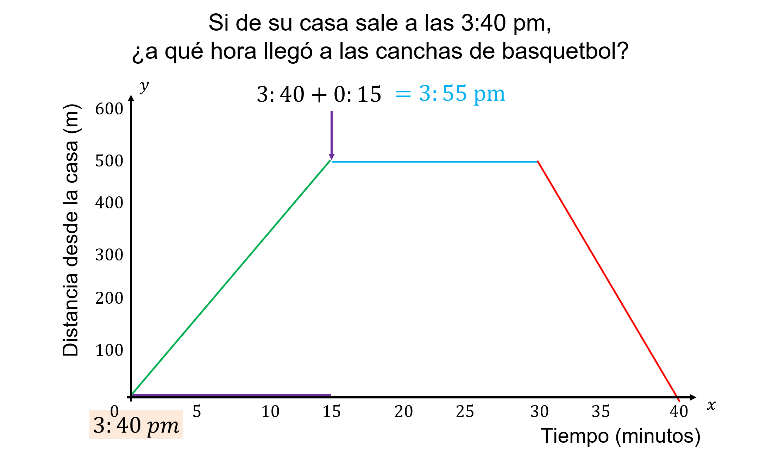
En la gráfica se observa el primer recorrido de 15 minutos para llegar a las canchas de basquetbol.
Si salió a las 3:40 de la tarde, al sumar los 15 minutos, Ángel llegó a las canchas a las 3:55 pm.
¿Qué se puede decir acerca del desplazamiento de los 30 a los 40 minutos?
Observa el segmento: es una línea recta decreciente, la cual representa el momento de regreso de Ángel a su casa.
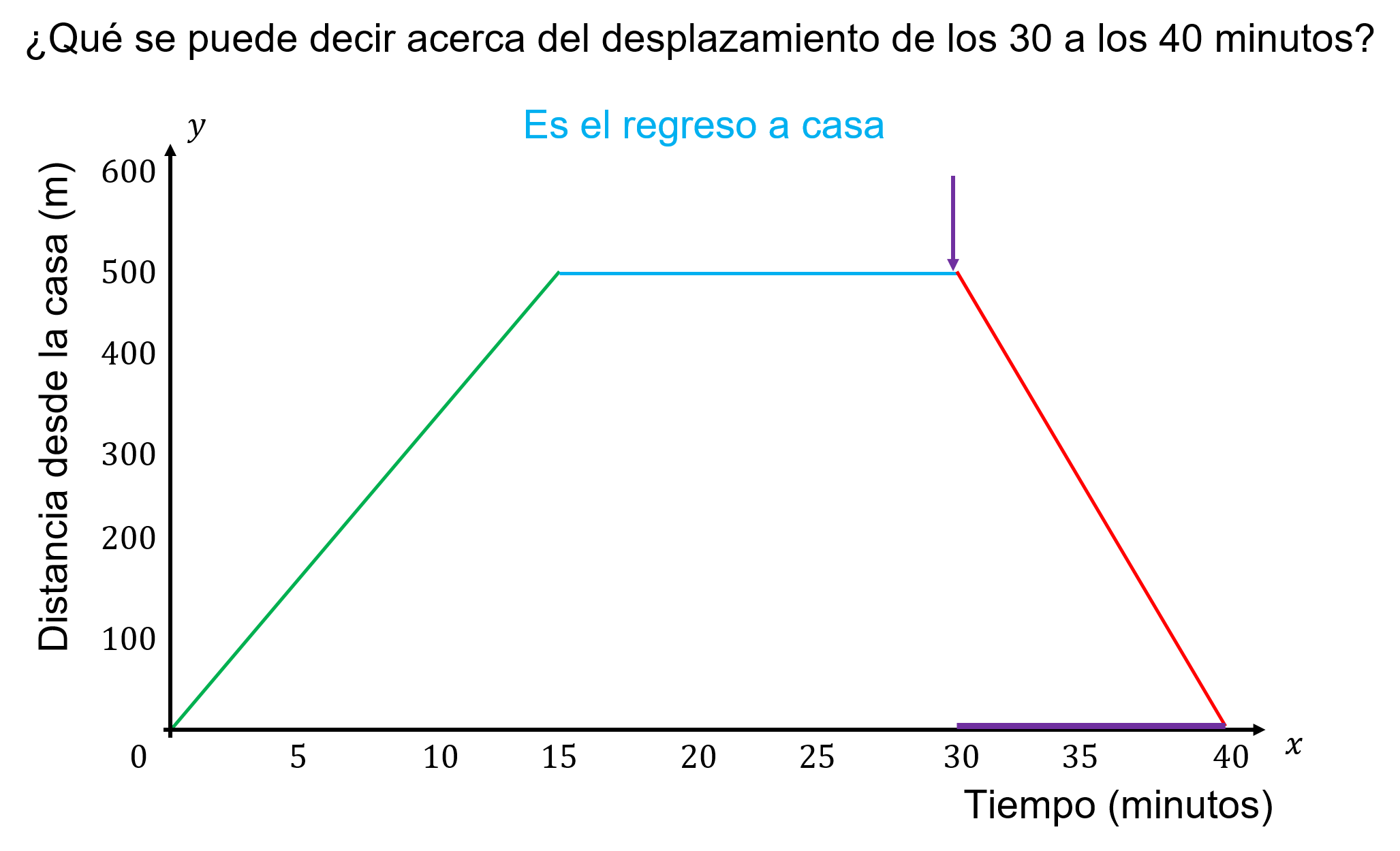
La gráfica analizada representa el traslado de Ángel desde su casa al entrenamiento y de regreso; implica una situación de movimiento al involucrar tiempo y distancia, que se le conoce como gráfica por secciones.
Al analizar las secciones de la gráfica, se tiene:
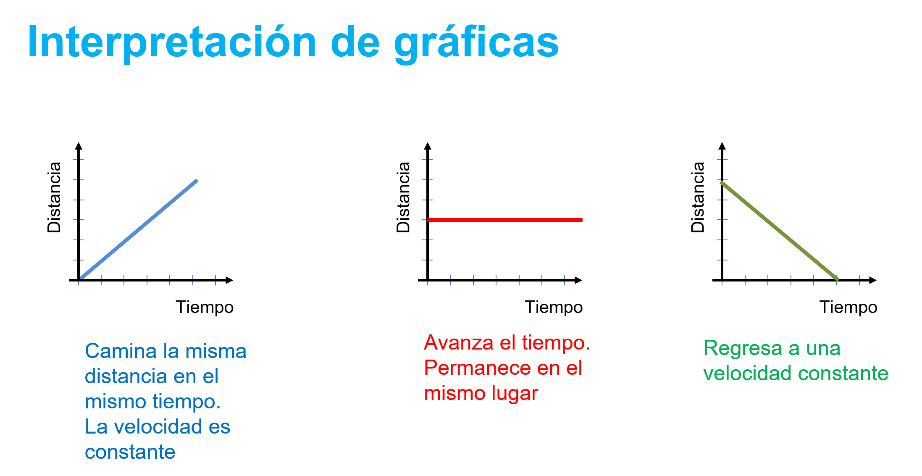
La primera gráfica representa un crecimiento constante. En términos del problema, significa que avanza la misma distancia en el mismo tiempo: camina sin incrementar ni disminuir la velocidad y no se detiene.
La segunda gráfica indica el incremento del tiempo, pero el valor en el eje “y” es el mismo. Es decir, indica que estuvo esperando.
Y la tercera gráfica representa un decremento constante. Es decir, caminar de regreso sin cambiar la velocidad ni parar.
Una gráfica de secciones de rectas suele componerse por al menos dos de estas tres gráficas.
Analiza una situación representada por una gráfica de secciones de rectas y curvas
Dos automóviles, “A” y “B”, parten juntos hacia la misma dirección.
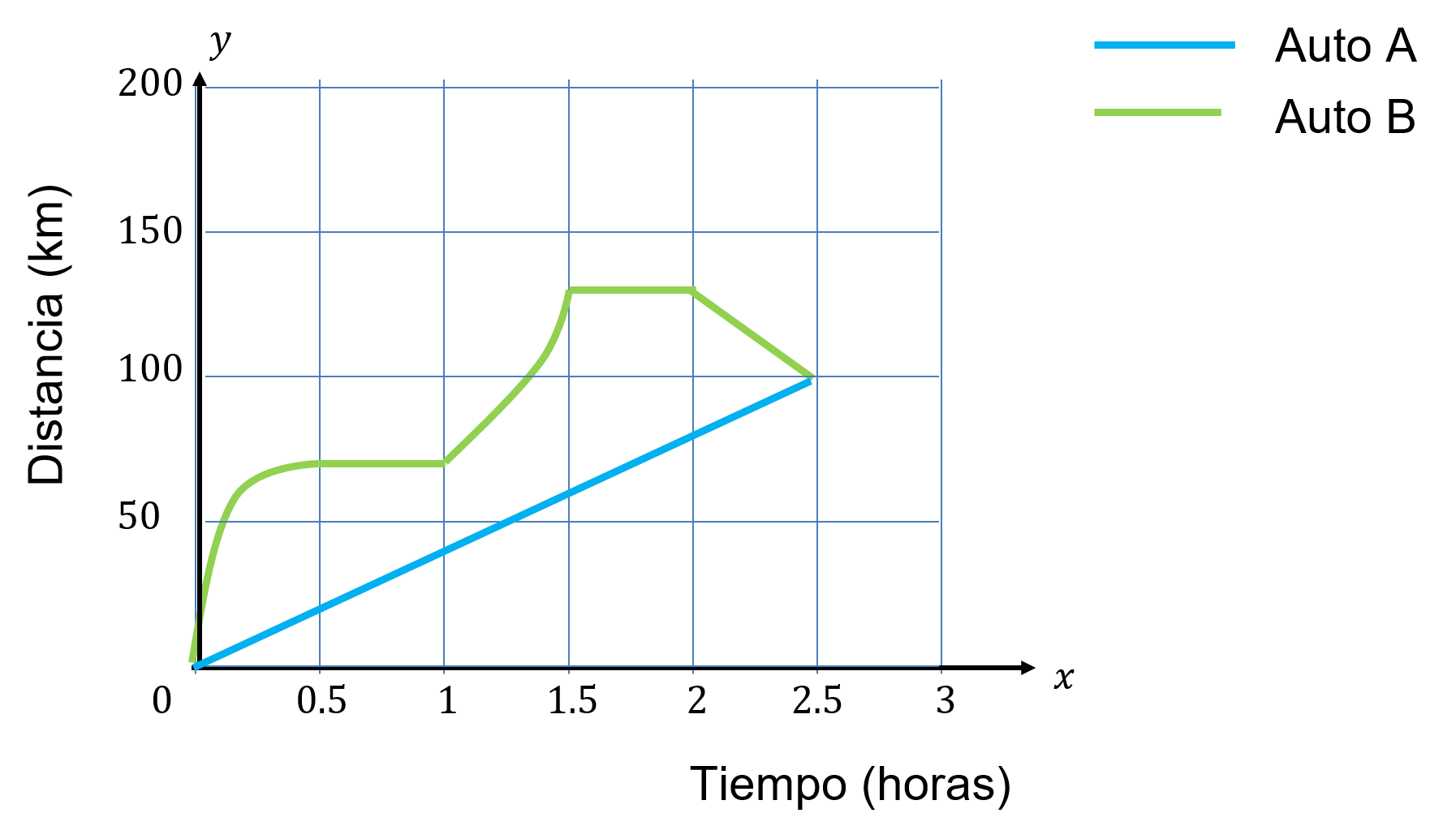
Las gráficas relacionan, para cada caso, el tiempo de recorrido con la distancia desde el punto de salida.
Con base en la gráfica, responde las siguientes preguntas:
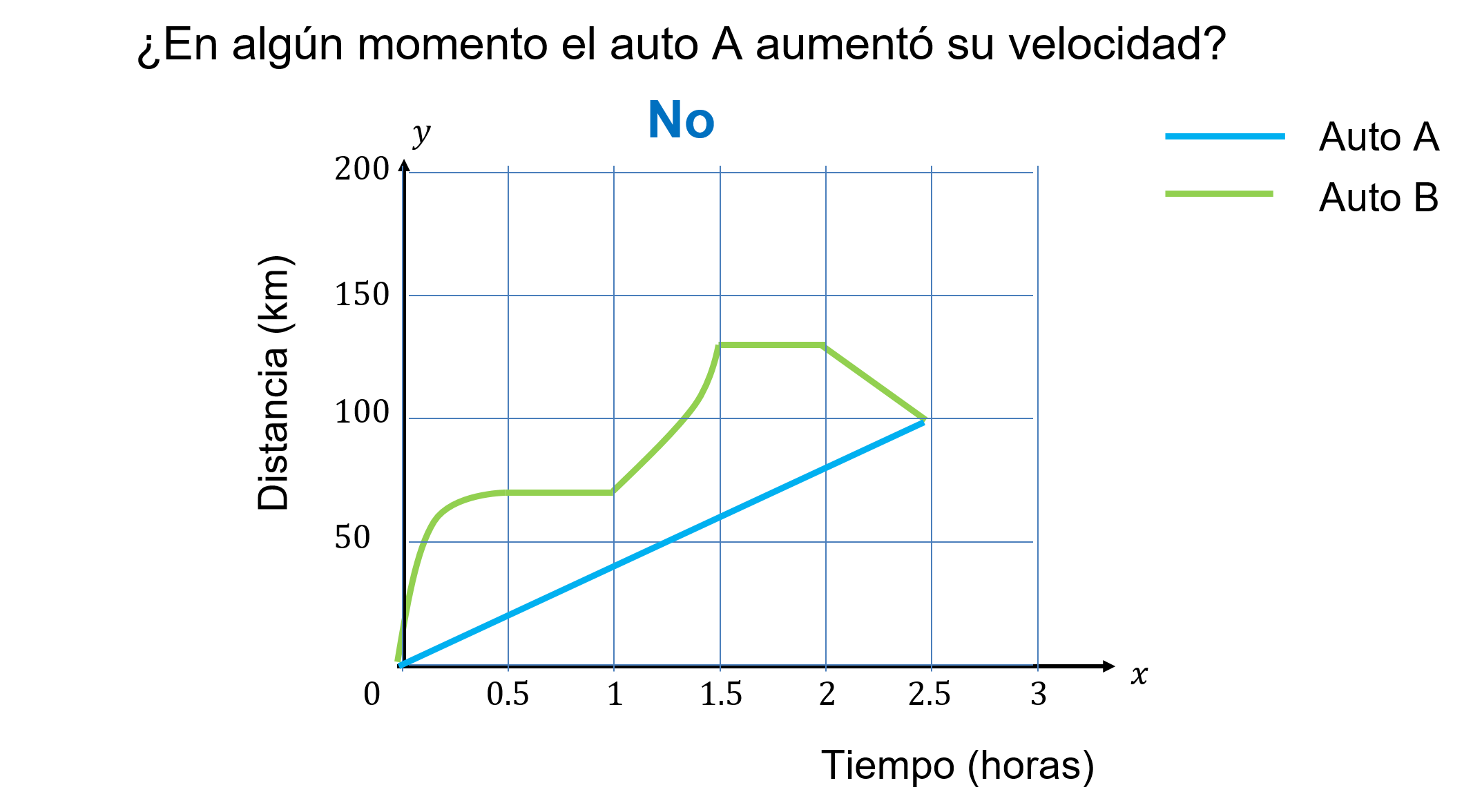
¿En algún momento el auto “A” aumentó su velocidad?
En la gráfica del auto “A”, la recta es constante y creciente. Por lo tanto, el auto no aumentó su velocidad.
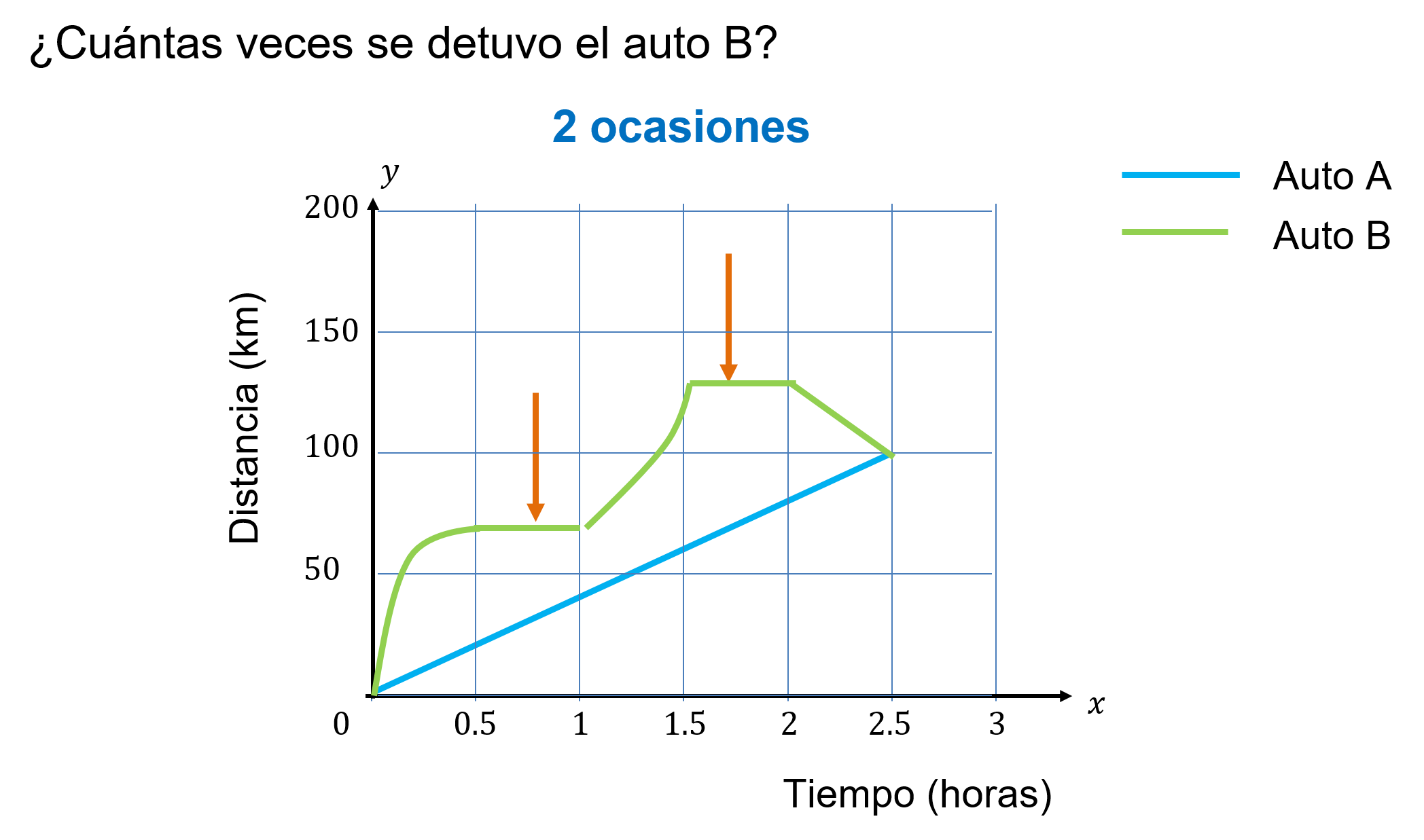
¿Cuántas veces se detuvo el auto “B”?
En la gráfica se observan 2 secciones de recta horizontal, y representan las 2 veces cuando el auto “B” se detuvo.
Si el auto “B” se detuvo en dos ocasiones, ¿a qué distancia del origen se detuvo la primera vez? y ¿a qué distancia del origen se detuvo la segunda vez?
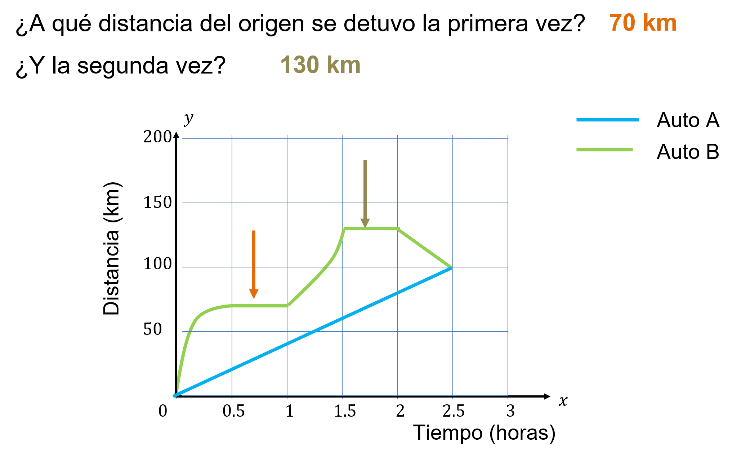
El primer segmento de recta donde se detuvo fue a 70 km.
El segundo segmento de recta se encuentra a 130 km.
¿Los dos autos se encontraron en algún punto?, ¿cómo podrías saberlo?
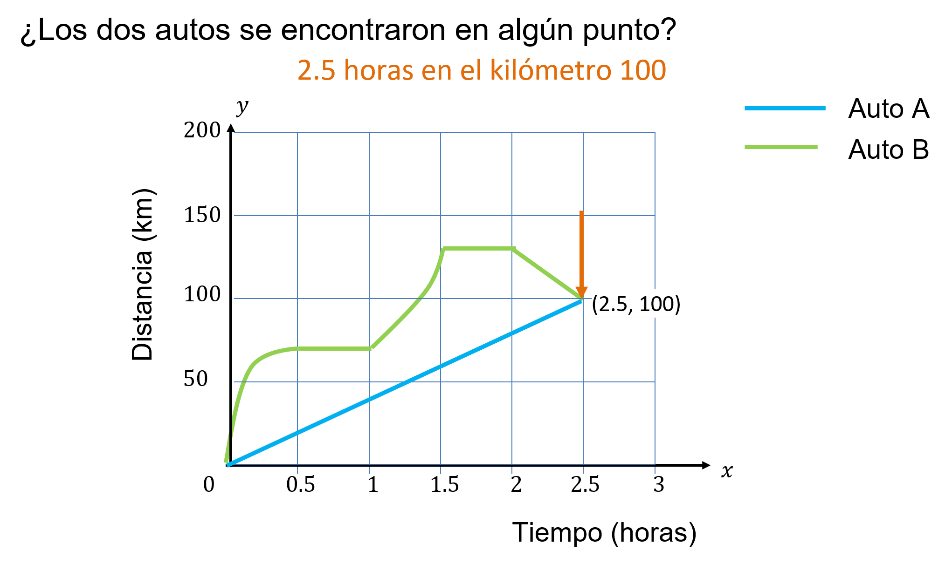
Para resolverlo, observa el punto donde se cruzan ambas gráficas.
Es decir, en la coordenada (2.5, 100).
En otras palabras, ambos autos se encuentran, en 2 horas y media, a una distancia de 100 km.
Al observar las gráficas de los dos autos, se concluye:
Que sólo la gráfica del auto “B” es una gráfica de secciones de rectas y curvas.
A continuación, una situación más de movimiento mediante gráficas de secciones.
Nurit y Manuel escalaron una montaña y utilizaron unos chips para registrar sus movimientos.
Aunque iban juntos, cada uno subió a su propio ritmo.
En algunas ocasiones hicieron descansos y en otras subían más rápido o más lento.
Como parte de la excursión, les entregaron las gráficas de los recorridos, indicando el tiempo y la distancia, pero con un pequeño detalle: no anotaron su nombre en las gráficas.
De este modo, Nurit y Manuel quieren identificar cuál es su respectiva gráfica.
Analiza cada una de las gráficas para determinar cuál es la de Nurit y cuál es la de Manuel.
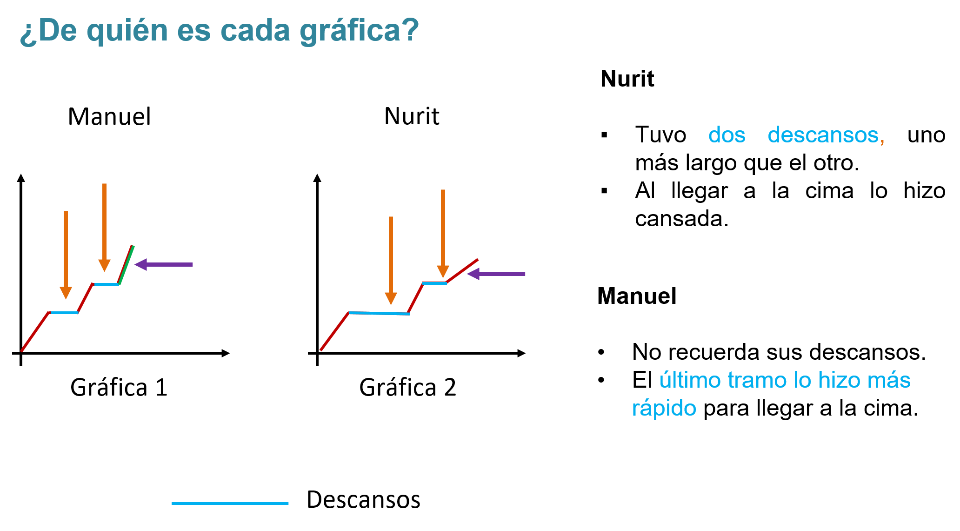
Nurit comenta que durante el trayecto tuvo dos descansos, uno más largo que otro. Para llegar a la cima lo hizo ya cansada.
Manuel no recuerda cuántos descansos tuvo, sólo que el último tramo lo hizo más rápido que Nurit porque quería llegar primero a la cima.
Los descansos en las gráficas se identifican con líneas horizontales, donde indican el tiempo transcurrido sin avanzar o retroceder una distancia.
En la gráfica 1 hay dos descansos; en la gráfica 2 también hay dos descansos.
Es decir, en ambas gráficas existe el mismo número de descansos. Sin embargo, en la gráfica 2 el primer descanso fue más largo.
Si se observa el último tramo de ambas gráficas, Manuel mencionó subir más rápido que Nurit.
En la gráfica 1, la última sección de recta tiene una mayor inclinación o pendiente, a diferencia de la segunda gráfica. Esto indica que se avanzó una distancia mayor en menor tiempo.
Por lo tanto, la primera gráfica corresponde a Manuel, quien mencionó ir más rápido que Nurit en el último tramo. Y la gráfica 2 corresponde a Nurit.
Ahora son unos alpinistas profesionales quienes escalan excelente.
Traza la gráfica del recorrido.
Como tienen una excelente condición física, suben rápido la ladera y en poco tiempo recorren una larga distancia.

Se detienen al ver que alguien necesita ayuda unos metros más abajo, y descienden para auxiliarlo.
Retoman el camino y suben aún más rápido para compensar el tiempo que bajaron.
Sólo falta considerar el tiempo invertido en ayudar cuando bajaron, así que traza una línea horizontal antes de volver a subir.
Has trazado la gráfica de secciones de recta.
Si se tuvieran los datos exactos de cuántos metros se subieron o bajaron, y en cuánto tiempo, se trazaría de acuerdo con esa información.
Observa el siguiente video del minuto 06:28 al 09:20
- Interpretación de gráficas formadas por segmentos
https://www.youtube.com/watch?v=MdbYXSsGKfo
¿Alguna vez has jugado carreritas con tus hermanos, primos o amigas?
¿Has subido a un transporte público para trasladarte a un lugar?
¿O has estado en un carrusel de la feria?
Las situaciones anteriores ilustran la variación del movimiento y, por lo regular, si realizas las gráficas correspondientes resultan gráficas de secciones de rectas y curvas.
En la vida cotidiana, ¿en qué otras situaciones de movimiento resulta una gráfica de secciones de rectas y curvas?
Comparte con tu familia tus respuestas.
¿Te has preguntado cómo se escriben algebraicamente las gráficas por secciones?
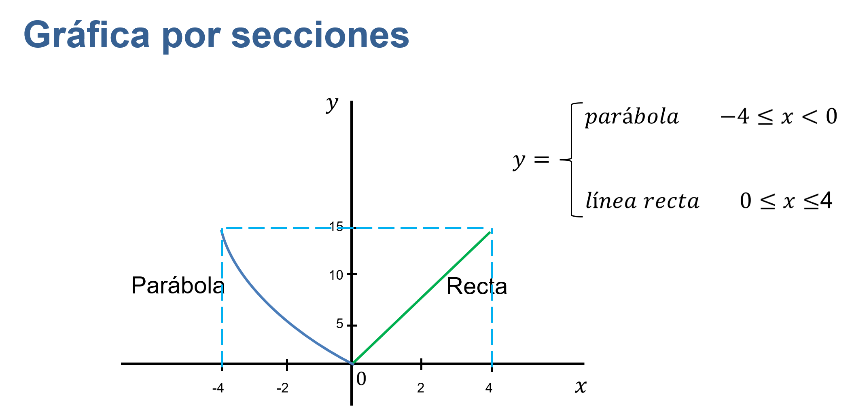
Considera el primer caso.
Aunque no se dan las ecuaciones, se observa que:
- La parábola sobre el eje de las “x” va de 4 negativo a cero; y sobre el eje de las “y” va de cero a 15 positivo. Esta es la primera sección de la gráfica.
- La línea recta sobre el eje de las “x” va de cero a 4 positivo; y sobre el eje de las “y” va de cero a 15 positivo. Esta es la segunda sección de la gráfica.
Entonces, se tiene que “y” es igual a:
- La ecuación de la parábola, cuando “x” está en el intervalo de 4 negativo a 0.
- Y la ecuación de la recta, cuando “x” va de 0 a 4 positivo.
Para cada intervalo en el eje de las “x”, se describe cómo es el comportamiento de la gráfica en el eje de las “y”.
Recapitula lo aprendido en la sesión.
Aprendiste cuáles son las gráficas de secciones de rectas y curvas; analizaste su utilidad para representar situaciones que modelan fenómenos reales, con las características de que no necesariamente siguen un patrón definido, o fórmula única. Por ejemplo: la velocidad de un automóvil en términos de tiempo, el trayecto de ir a un lugar y de regreso, o el movimiento descrito de un insecto, entre otros.
Aprendiste a construir gráficas por secciones: primero se determinó el intervalo sobre el eje de las “x” en el plano cartesiano, y después se encontraron los valores sobre el eje de las “y”. Y, finalmente, se repite el procedimiento para las siguientes secciones.
Lo anterior con el propósito de interpretar las gráficas de secciones de rectas y curvas, siendo indispensable analizar los segmentos que la forman.
Con lo antes expuesto, lograste leer y elaborar gráficas formadas por secciones rectas y curvas que modelan situaciones de movimiento.
Aplica lo aprendido en la sesión al responder las siguientes 3 preguntas. Se te sugiere que anotes tus respuestas en el cuaderno, y verifica tus resultados al final.
Pregunta 1. Las siguientes gráficas representan la altura que alcanza un elevador en movimiento en función del tiempo.
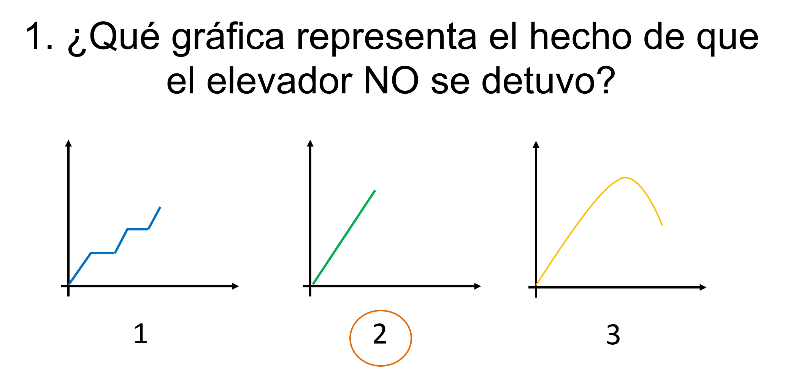
¿Es la gráfica 1, la gráfica 2 o la gráfica 3?
¿Qué gráfica representa el hecho de que el elevador no se detuvo?
Si tu respuesta es la gráfica 2 estás en lo correcto.
Pregunta 2. Si la gráfica representa la velocidad de un móvil en términos del tiempo.
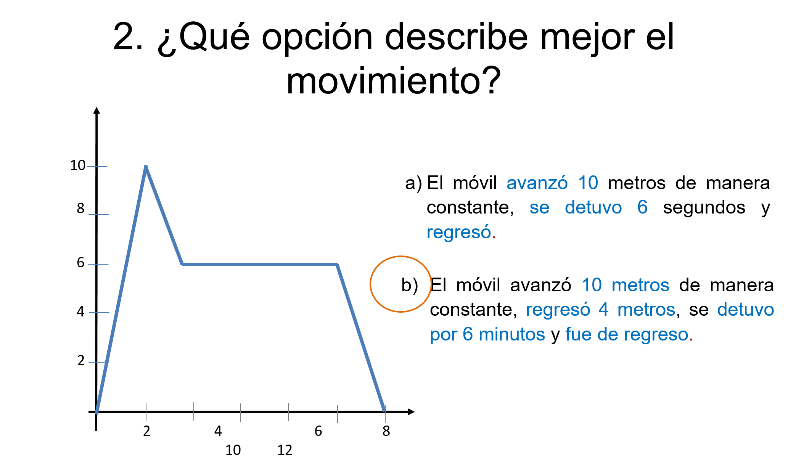
¿Cuál de las 2 opciones describe mejor el movimiento representado en la gráfica? ¿Inciso “a” o inciso “b”?
Si tu respuesta fue el inciso “B”, estás en lo correcto.
Pregunta 3: Gerardo y su hija Julieta hicieron un globo aerostático casero. Para soltarlo fueron a un lugar llamado San Miguel Regla, en Hidalgo.
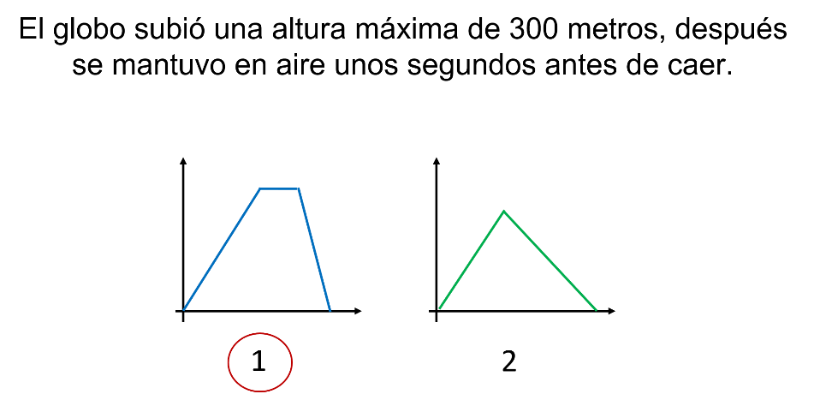
¿Cuál de las siguientes gráficas representa mejor esta situación? Observa bien las secciones de recta en ambas gráficas.
La respuesta correcta es la gráfica 1.
Si tienes dudas o quieres ejercitar lo aprendido te puedes apoyar en tu libro de texto.
Se te sugiere buscar en el índice del bloque 3 el aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
El reto de hoy:
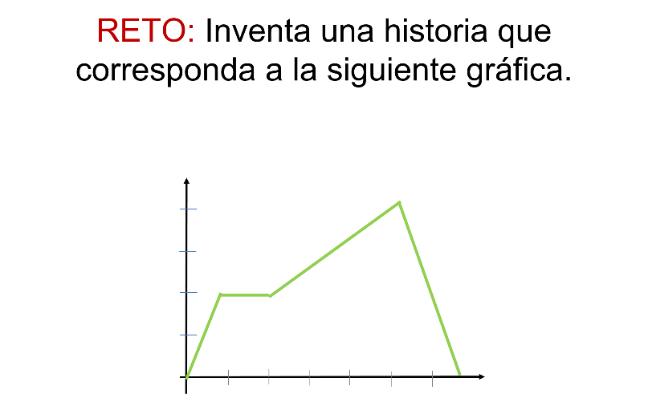
Traza en tu cuaderno la siguiente gráfica e inventa una historia que corresponda a la representación: ¿qué situación se te ocurre?, ¿qué trayecto o actividad puede representarse en la gráfica?
Cuando termines, comparte la historia que inventaste y comprueba si corresponde a la gráfica
¡Buen trabajo!
Gracias por tu esfuerzo.