Problemas cotidianos de congruencia y semejanza de triángulos
Problemas cotidianos de congruencia y semejanza de triángulos
Aprendizaje esperado: resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.
Énfasis: explicitar los criterios de congruencia y semejanza de triángulos a partir de construcciones con información determinada.
¿Qué vamos a aprender?
Con la explicitación de los criterios de congruencia y semejanza de triángulos a partir de construcciones con información determinada, podrás poner manos a la obra en el uso de estas herramientas y resolverás problemas de congruencia y semejanza.
Elabora tu propio resumen anotando los datos importantes o nuevos que identifiques durante la sesión.
Registra las dudas, inquietudes o dificultades que surjan al resolver los planteamientos. Éstas las puedes resolver al revisar tu libro de texto.
Los triángulos son los polígonos con menor número de lados que existe en la geometría plana.
La humanidad tiene documentos de su estudio desde hace aproximadamente 4000 años. Basta con observar algunas de las edificaciones más sorprendentes del mundo antiguo:
Las pirámides de Egipto, construidas como criptas reales, para los faraones desde el año 2700 antes de nuestra era.
Los triángulos están presentes en muchos ámbitos de nuestra vida cotidiana, en juguetes simples o la forma en que se generan los escenarios virtuales y mundos completos de tus videojuegos y películas favoritas.
También los puedes encontrar en la diferente simbología urbana a tu alrededor donde se advierte de un riesgo.

Y así como los egipcios, la arquitectura moderna y el arte siguen usando esta figura como base de su construcción, no solo por sus grandes propiedades, también por su versatilidad y resistencia. Seguramente conoces al escultor mexicano, originario del estado de Chihuahua, Enrique Carbajal González, mejor conocido como Sebastián por una de sus obras más icónicas. Cabeza de Caballo, escultura exterior de acero de 28 metros de alto, instalada en Paseo de la Reforma, Centro de la Ciudad de México. Podrás notar que los triángulos forman la mayor parte de la estructura.

Con una altura de 128 metros fue el segundo rascacielos más alto de México por casi dos décadas. Su cara frontal, la forma un triángulo isósceles y las caras laterales de este prisma se dividen en tres triángulos, dos de ellos congruentes.
En su interior las columnas de soporte hechas de acero también forman un entramado triangular que se puede observar por sus ventanas y hasta la parte superior de la torre.

como este icosaedro estrellado, que se forma con 60 triángulos isósceles congruentes entre sí.
El estudio formal de los triángulos ha permitido su uso en formas tan variadas como las que acabas de observar y faltan muchas más por describir o tal vez de inventar, si aprendes a estudiarlo de forma correcta.
¿Qué hacemos?
Para lograrlo, comenzarás identificando un poco de la forma que has estado utilizando en matemáticas para referirnos a ellos y a sus componentes.
En este triángulo,
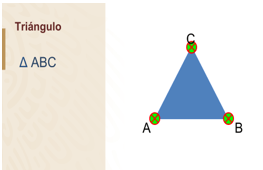
a cada vértice lo identificas con una letra mayúscula, y nombrarás a este el triángulo ABC.
Puedes utilizar cualquier letra del abecedario y utilizaremos A’, B’ y C’ si los quieres asociar a otra figura, indicando que hay algún tipo de correlación entre estos vértices.
Si quieres referirte al valor de los ángulos como una incógnita, se acostumbra a usar las letras minúsculas del alfabeto griego.

Es muy importante en el lenguaje de las matemáticas, como en cualquier otro lenguaje, saber expresarte correctamente y así, las personas y tú mismo tendrán una mejor comprensión de lo que se hace, se estudia y se entiende.
Analiza el siguiente diagrama para ejemplificar lo que acabas de aprender:
En el interior del cuadrilátero BCDE se forman
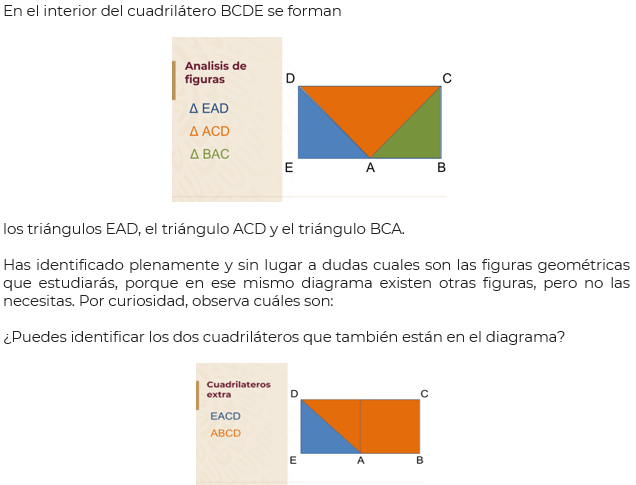
El primero es el formado por los vértices EACD y el segundo cuadrilátero es el formado por los vértices ABCD.
Ahora, los ángulos, y para identificarlos de manera correcta usarás dos formas de referirse a ellos.
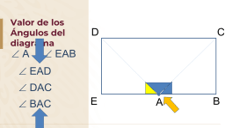
Si haces referencia al ángulo en el vértice A, y el análisis en curso es del interior del cuadrilátero, entonces el ángulo BAE es este y mide 180°
Al referirnos a este ángulo BAE debes tener cuidado de ubicar en el medio la letra del vértice donde se encuentra el ángulo. En este caso el vértice A.
Identifica otros ángulos de esta forma en la imagen anterior.
Ése, es el ángulo DAE; ese, es el ángulo DAC y éste es el ángulo BAC
Los tres ángulos tienen en común el vértice A y en los tres está la letra A escrita en medio de las tres letras.
También denotamos el valor de un ángulo por las letras griegas que acabas de observar y las utilizas de la siguiente manera:
El valor del ángulo ADC es igual a beta y el valor de alfa es de 40°
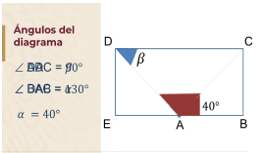
Nota que alfa y beta representan los valores de la medida del ángulo, no su posición en el diagrama.
Por último, indica algunos otros ángulos con valores aleatorios.
Ángulo DAC es igual a 90°, el ángulo DAB es igual a 130°. Comienza con el rectángulo ABCD.
Cuando lees “Rectángulo ABCD” debes tener en mente todas las propiedades de esa figura, por ejemplo, es importante que recuerdes que todos los ángulos internos miden 90°, que es un paralelogramo, es decir sus lados opuestos son paralelos entre sí, además el segmento de recta AB es igual al segmento de recta DC y el segmento de recta BC es igual al segmento AD.
La siguiente indicación es que P es el punto medio del segmento DC, lo que indica la aparición de nuevos segmentos, el segmento DP y el segmento PC, que por ser P un punto medio, entonces DP y PC tienen la misma medida y no necesitas de un valor que lo afirme.

y su clasificación por sus lados:
- Equilátero con tres ángulos y lados iguales
- Isósceles con dos ángulos y lados iguales
- Escaleno con 3 ángulos y lados distintos
Puedes hacer diferentes afirmaciones de la siguiente figura.
Identifica 4 triángulos dentro del rectángulo, el triángulo rectángulo ADG, triángulo GAF, el triángulo rectángulo ABE. También identifica los cuadriláteros ABCD que es rectángulo, y los cuadriláteros AECF, y ABCG, entre otros.
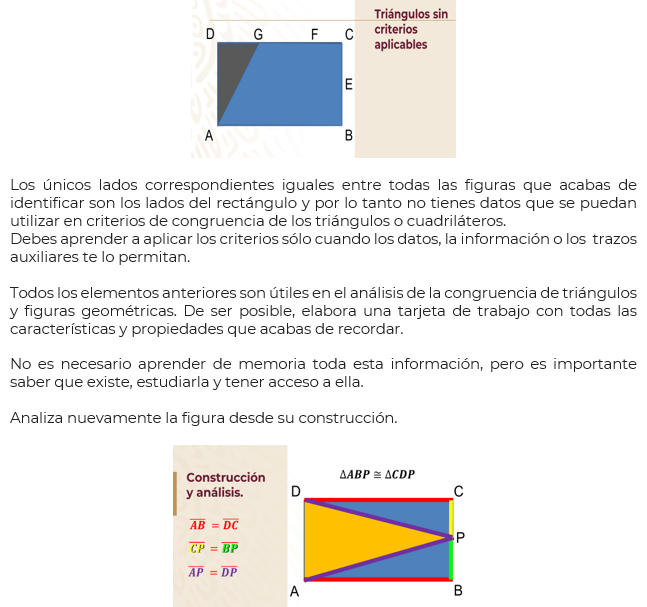
Traza el rectángulo ABCD. Marca P que es punto medio de BC y traza los segmentos AP y DP. Identifica los triángulos que se formaron junto con algunas características.
Triangulo APD es isósceles porque el segmento AP = DP y puedes afirmar esto porque P es punto medio del segmento BC.
El triángulo ABP es triángulo rectángulo porque tiene un ángulo de 90° heredado del rectángulo inicial. Su lado BP mide un medio de BC. El triángulo CDP es triángulo rectángulo porque tiene un ángulo de 90° heredado del rectángulo inicial. Su lado CP mide un medio de BC.
¿Notaste que el triángulo ABP y el CDP comparten las mismas características?
Puedes usar el criterio LLL para verificar la congruencia de ambos triángulos.
AB = CD porque son lados opuestos de un rectángulo.
AP=DP porque son lados de un triángulo isósceles
Comprobadas las igualdades de lados correspondientes aseguras que el triángulo ABP es congruente con el triángulo CDP
La congruencia de éstos mismos triángulos los puedes verificar a partir del criterio de congruencia LAL, llegando a la misma conclusión.
El criterio LAL nos asegura que dos triángulos son congruentes si tienen dos lados correspondientes iguales y el ángulo comprendido entre ellos es igual.
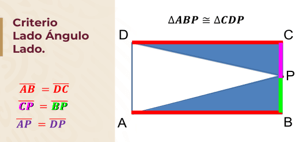
Primero encuentra los lados correspondientes iguales con la información que tienes.
El segmento AB es igual al segmento DC porque la figura ABCD es un rectángulo.
El segmento CP es igual segmento BP porque P es punto medio del segmento DC.
Y el ángulo comprendido entre esos dos lados es igual a 90 grados, en ambos casos Ángulo PBA es igual al ángulo DCP igual a 90°.
Ya cuentas con todos los componentes del criterio LAL para poder afirmar que los triángulos ABP es congruente con el triángulo CDP.
¿Sabes por qué escogimos esta figura para su análisis?

Resulta que es semejante a una de las caras del prisma triangular de la torre Insignia.
¿El arquitecto pensaba en esta congruencia cuando realizó el diseño del edificio?
Para hablar de semejanza, como el diagrama anterior y el edificio, recuerda cuales son las características de las figuras semejantes y cómo se construyen.
De forma puntual la semejanza de figuras geométricas reside en conservar ángulos y proporción entre sus lados, lo que asegura que las figuras son iguales, pero de diferente tamaño.
En realidad, la mayor parte de las veces que se utilizan estos conocimientos es en el área de la construcción, la ingeniería, la arquitectura, el arte, la informática, etcétera.
Imagina la siguiente situación:
En este diagrama se muestra una casa, un edificio y el patio que los separa, que es propiedad de la casa.
Se va a instalar un calentador de agua solar, pero como la casa tiene techo de 2 aguas se debe montar en otra estructura. El dueño de la casa exige que la estructura para instalar el calentador sea de la menor altura posible. Para lograrlo, el técnico de
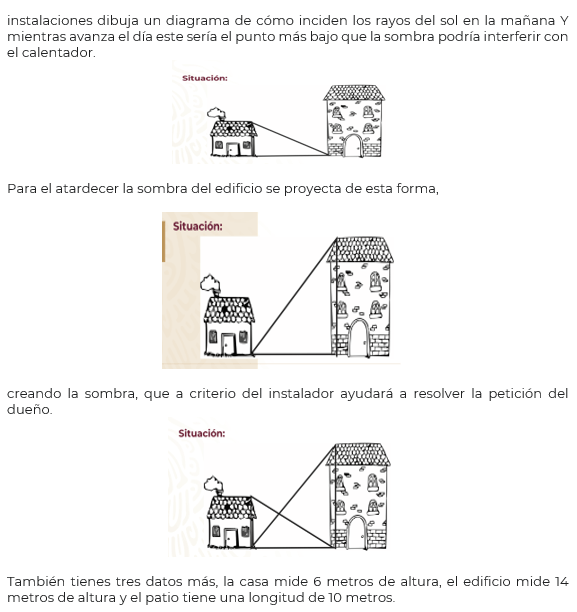
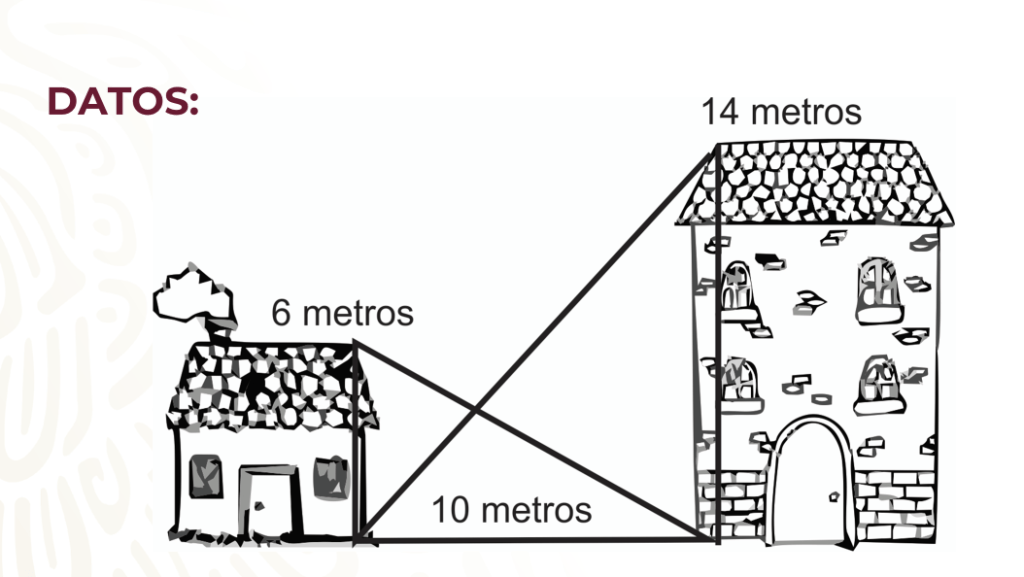
Si observas que la altura se encuentra en el punto donde se interceptan las sombras puedes cumplir con las exigencias del dueño y asegurarte que el calentador de agua tendrá la mayor cantidad de exposición al sol con la menor altura posible.
Traslada el diagrama a tu cuaderno y ocupando los datos anteriores puedes hacer el análisis geométrico y numérico de la situación.
En esta situación, utilizarás el hecho de que se formaron triángulos semejantes para poder analizar con expresiones algebraicas lo propuesto por el técnico de instalación.
El reto de hoy:
Te proponemos que analices con tu familia y compañeros, si existe otro punto donde recibiría la mayor cantidad de luz el calentador solar, manteniendo la altura de la estructura al mínimo.
Revisa tus libros de texto para afirmar, rectificar o consultar tus posibles dudas, así como resolver los ejercicios propuestos en el tema de semejanza y congruencia de triángulos.
¡Buen trabajo!
Gracias por tu esfuerzo.