El rango
El rango
Aprendizaje esperado: usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana), el rango y la desviación media de un conjunto de datos y decide cuál de ellas conviene más para el análisis de los datos en cuestión.
Énfasis: usar e interpretar el rango de distintos conjuntos de datos y su relación con la dispersión de los mismos.
¿Qué vamos a aprender?
Continuarás con el estudio de las medidas de tendencia central. En esta sesión, profundizarás en otra medida que se puede obtener de los datos de un conjunto numérico, el rango. Por lo que, analizarás y reconocerás su utilidad en diversas situaciones.
¿Qué hacemos?
Inicia esta sesión de matemáticas con la siguiente situación. Observa los siguientes conjuntos de números
El primer conjunto está formado por los números:
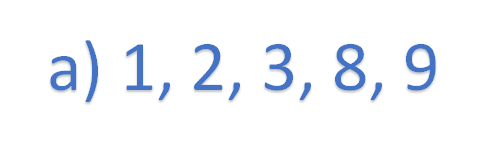
El segundo conjunto está integrado por los números:
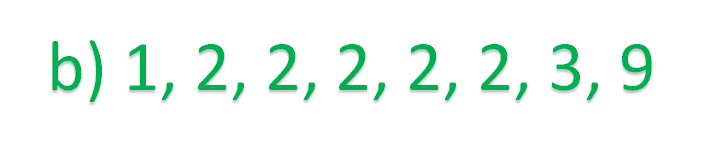
Y al tercer conjunto lo forman los números:
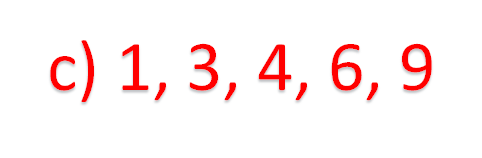
Ahora, reflexiona en lo siguiente: ¿te dicen algo estos números?, ¿qué pueden significar?, ¿qué tienen en común?, ¿crees que sean sucesiones numéricas?
Para dar respuesta a las interrogantes anteriores, imagina un contexto para estos números.
Contexto 1
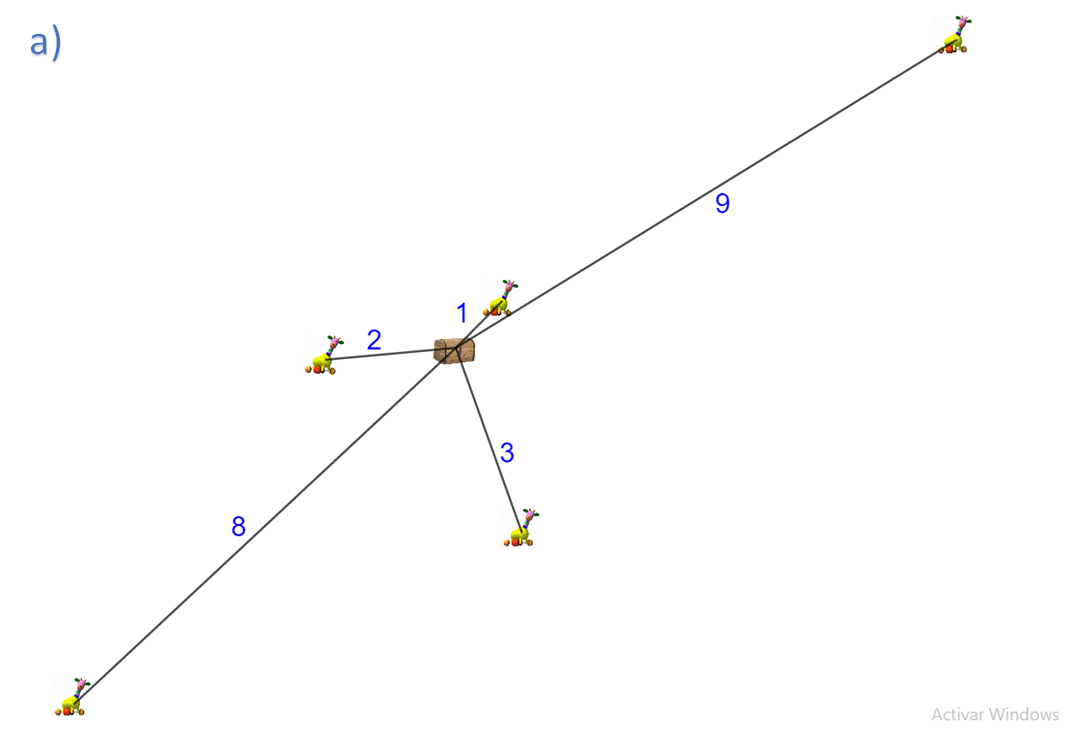
En una reunión familiar, algunos invitados tienen niños pequeños, los cuales, bajo la supervisión de 3 adultos, se pusieron a jugar en 3 áreas de juego distintas y dejaron los juguetes regados. En el centro de cada habitación se encuentra un baúl de madera que es donde se guardan los juguetes. Los conjuntos de números anteriores representan la distancia, en metros, a la que quedó cada uno de los juguetes respecto del baúl.
Es decir: en la primera habitación, cinco juguetes quedaron regados de la siguiente manera, a 1 metro de distancia del baúl, a 2 metros, a 3 metros, a 8 metros y a 9 metros, como se muestra en la siguiente imagen.
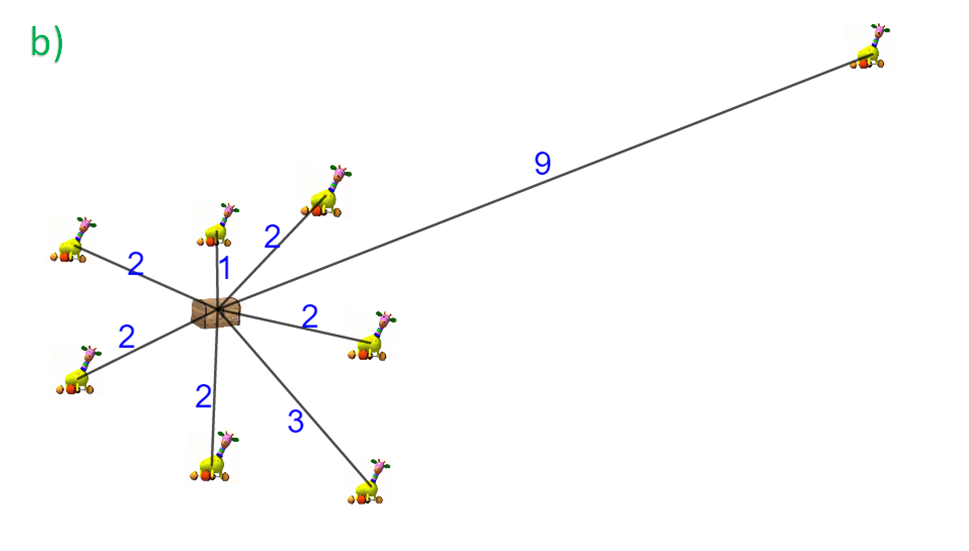
En la segunda habitación, 8 juguetes quedaron regados de la siguiente manera: 1 juguete a 1 metro de distancia, 5 juguetes quedaron a 2 metros de distancia, otro a 3 metros y el último a 9 metros de distancia, como se muestra en la siguiente imagen.
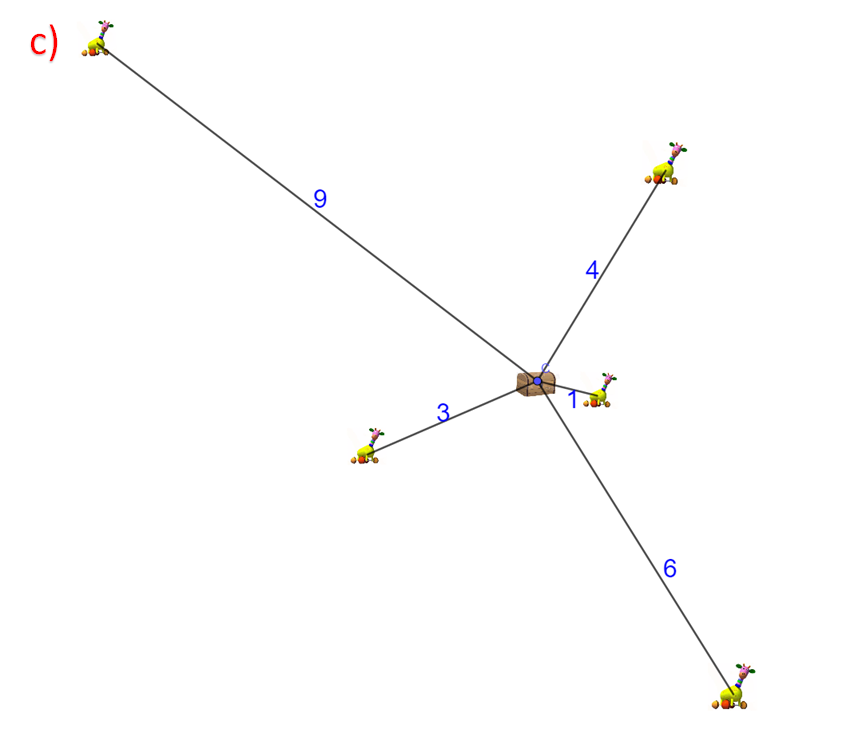
Por último, en la tercera habitación quedaron 5 juguetes regados de la siguiente manera: uno a 1 metro de distancia, otro a 3 metros de distancia, uno más a 4 metros de distancia, otro a 6 metros y uno a 9 metros, como se muestra a continuación.
Si te dieran a elegir una habitación para recoger los juguetes y guardarlos de nuevo en el baúl, ¿qué habitación elegirías?, ¿por qué? Justifica tu respuesta.
Observa las tres habitaciones juntas, puede que sea de utilidad para tomar una decisión.
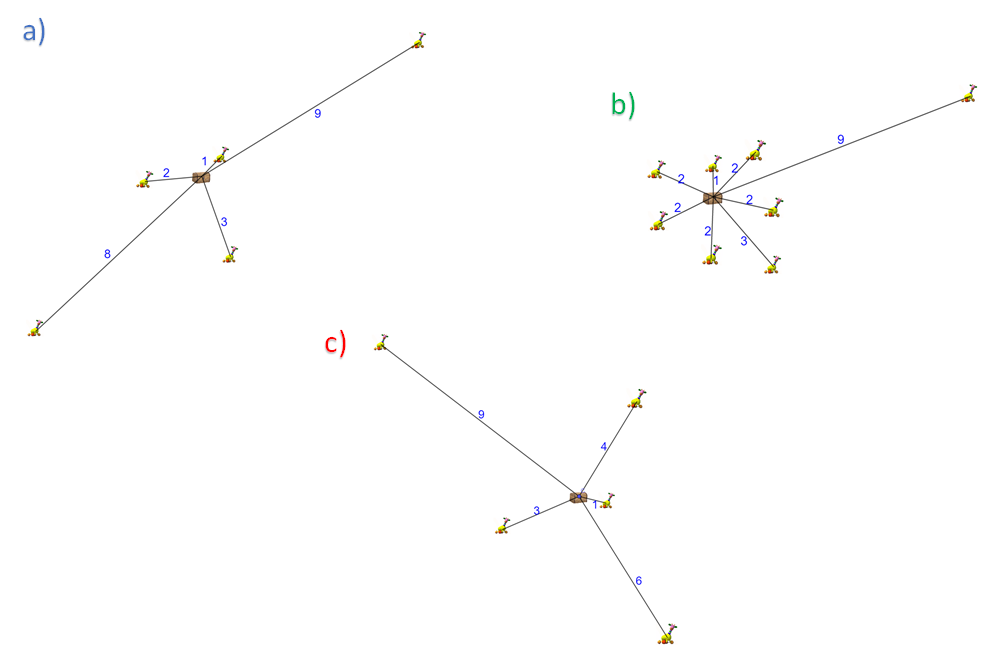
Aunque visiblemente puede que ya hayas elegido qué habitación ordenar, analiza la situación matemáticamente, para interpretar todo lo que los números puedan decir. Para ello, obtén las medidas de tendencia central de cada conjunto de datos.
Para el primer conjunto de datos y considerando que todas las cantidades se encuentran en metros, su media aritmética es de 4.6, ya que al sumar los números que lo integran y dividirlo entre 5, que es el número de datos, se obtiene ese valor.
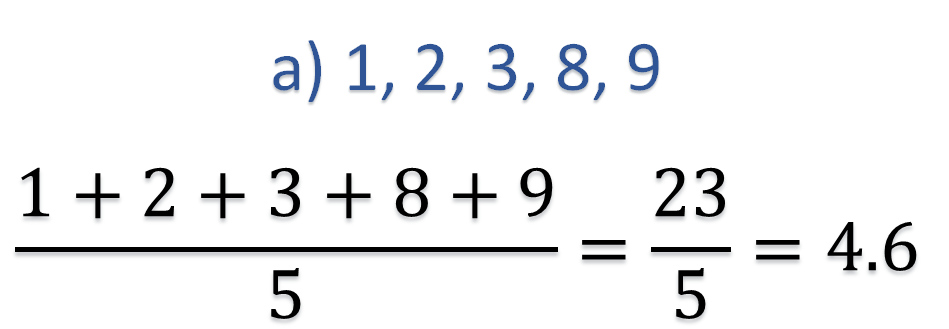
No tiene moda, puesto que no hay algún dato que tenga mayor frecuencia que los otros, y su mediana es 3 ya que, ordenando los datos de menor a mayor, el tres se encuentra en el centro.

Por lo tanto, para el primer conjunto las medidas quedan de la siguiente manera:
Media = 4.6
Moda = no hay
Mediana = 3
Para el segundo conjunto de datos, sin olvidar que los números representan la distancia en metros, de los juguetes al baúl, se tiene que su media aritmética es 2.875, ya que al sumar todos los números que lo integran y dividirlo entre 8, se obtiene ese valor.
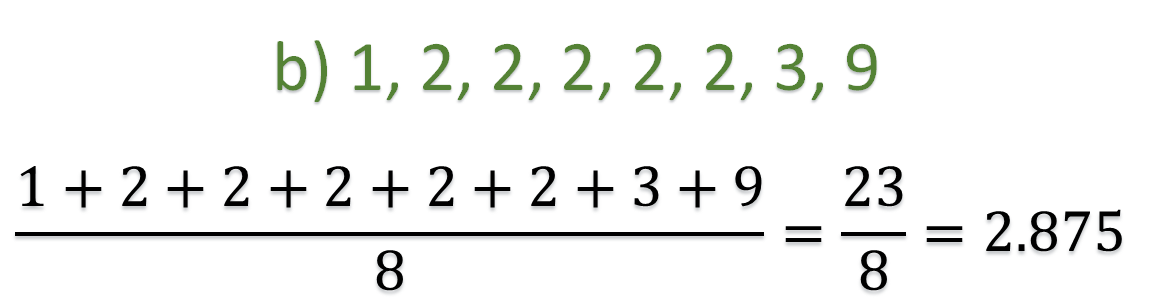
Su moda es 2, por ser el dato con mayor frecuencia, y su mediana es 2, ya que, al ordenar los datos de menor a mayor, el cuarto y el quinto número dos, quedan en el centro y su promedio es dos.

Por lo tanto, para el segundo conjunto las medidas quedan de la siguiente manera:
Media = 2.8775
Moda = 2
Mediana = 2
Para el tercer conjunto de datos de las distancias en metros de los juguetes al baúl, su media aritmética es 4.6, ya que al sumar los números que lo integran y dividirlo entre 5 se obtiene ese valor.
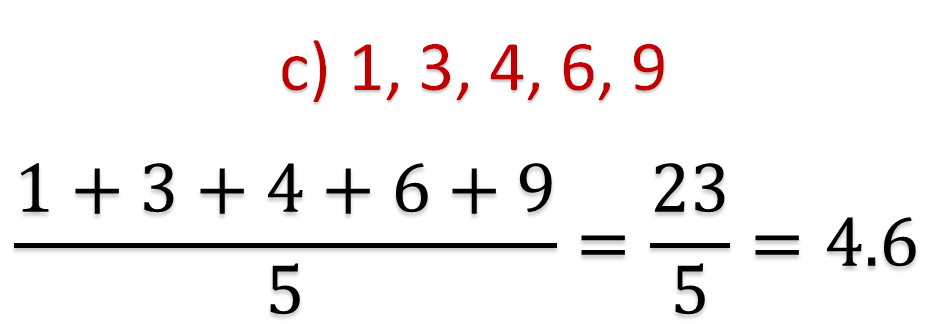
No tiene moda porque no hay un dato con mayor frecuencia, y su mediana es 4 ya que, al ordenar los datos de menor a mayor, el 4 queda al centro de ellos.

Por lo tanto, para el tercer conjunto las medidas quedan de la siguiente manera:
Media = 4.6
Moda = no hay
Mediana = 4
Otra medida que se puede obtener de los datos de un conjunto numérico es el rango.
El rango está definido como el intervalo entre los valores extremo máximo y mínimo del conjunto. Una manera de calcular el rango es determinar la diferencia entre esos valores, es decir, el valor máximo menos el valor mínimo.
Como puedes observar, cada conjunto de números se comporta de manera distinta, pero tienen cosas en común, por ejemplo, la suma de los datos de cada conjunto es 23, para el primer y tercer conjunto la media es la misma, es decir: 4.6
Además, todos los conjuntos de datos tienen el mismo rango. El dato menor de los 3 conjuntos es 1 y el mayor es 9; por lo tanto, 9 menos 1 es igual a 8 y ése es el rango de cada uno de los conjuntos.
En este caso, el rango no dice mucho del comportamiento de los conjuntos ya que en los 3, es el mismo y al menos en las imágenes de las habitaciones, se puede observar que las distribuciones son distintas entre sí, y es por ello que se debe continuar analizando qué pasa al interior de cada conjunto para resolver el problema.
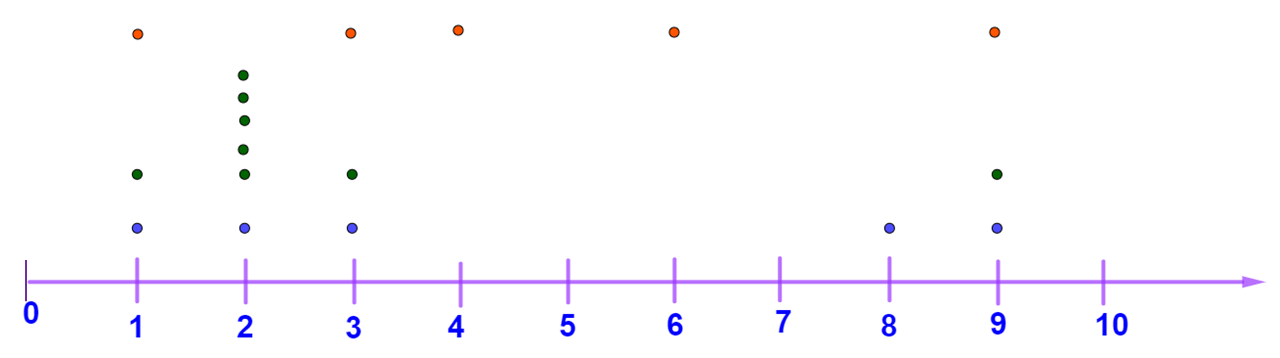
Ya observaste la distribución de los datos en las imágenes de las habitaciones, ahora la analizarás en la recta numérica.
En la primera habitación, los juguetes quedaron regados de la siguiente manera, a 1 metro de distancia del baúl, a dos metros, a 3 metros, a ocho metros y a nueve metros, como se muestra en la siguiente recta.

En la segunda habitación, los juguetes quedaron regados de la siguiente manera: uno a 1 metro de distancia del baúl, 5 juguetes quedaron a 2 metros de distancia, otro a 3 metros y el último a 9 metros de distancia, lo cual puedes ver en la siguiente recta.
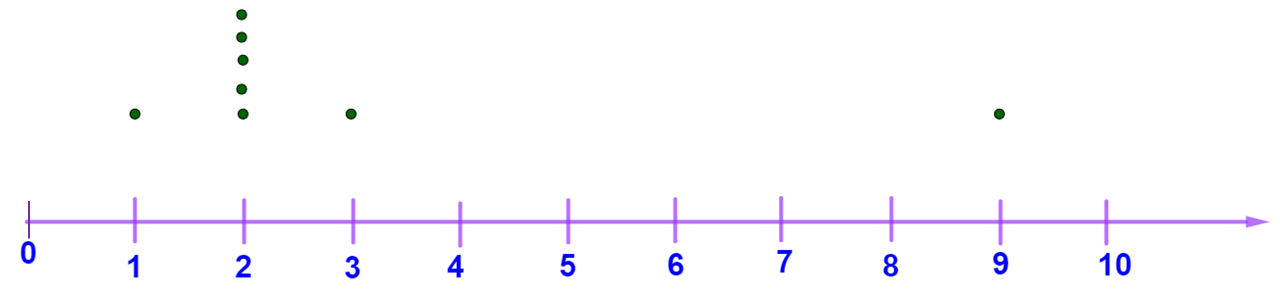
Por último, en la tercera habitación quedaron 5 juguetes regados de la siguiente manera: uno a 1 metro de distancia, otro a 3 metros de distancia, uno más a 4 metros de distancia, a 6 metros el siguiente y el último a 9 metros, como se puede observar en la siguiente imagen.
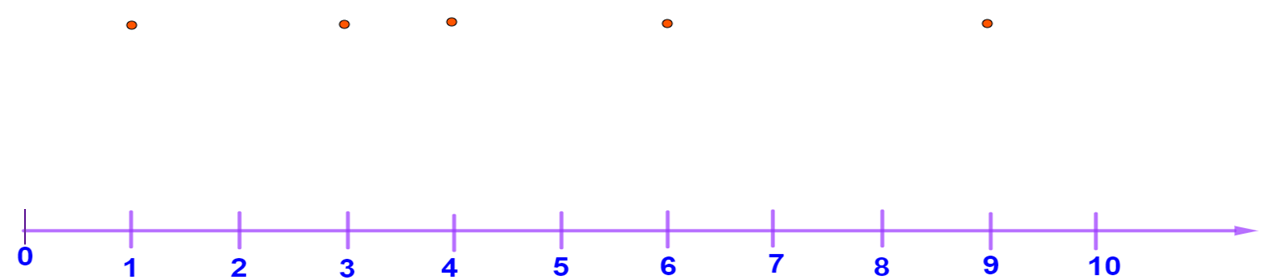
¿Cuáles de los tres conjuntos de datos consideras que están menos dispersos?, ¿cuáles consideras que están más dispersos?
Observa todos los puntos juntos superpuestos en la recta numérica.
Considera que, en dos de los conjuntos se tiene la misma cantidad de datos. Analiza qué ocurre en ellos tomando como referencia su media aritmética, que en ambos casos es 4.6.
En la siguiente imagen se traza una línea vertical que representa la media aritmética en 4.6 y, a partir de ella, se trazan las distancias a cada uno de los puntos que representan el lugar en donde se encuentran los juguetes con respecto al baúl en donde deben ser guardados.
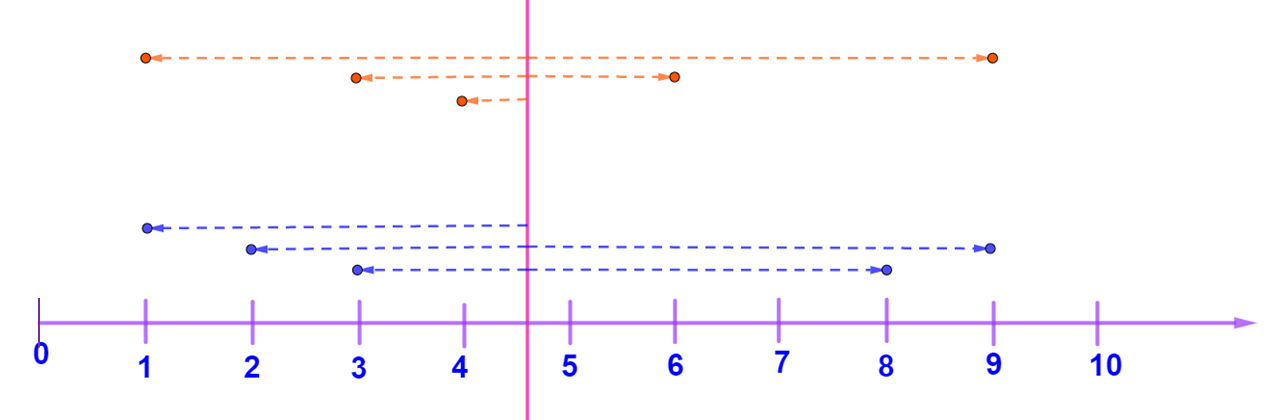
¿Con esta nueva representación modificarías la respuesta para identificar cuáles están más dispersos?
De la imagen anterior, se puede observar que, al tener la media aritmética como referencia, el conjunto de datos que representan los juguetes de la primera habitación están más dispersos que los de la tercera habitación, porque tienen entre todos, mayor distancia con respecto a la media.
Ahora, si se incluyen los datos de la segunda habitación, ¿qué dato se emplearía como referencia para observar las distancias? La media aritmética de este conjunto. Observa la siguiente imagen.
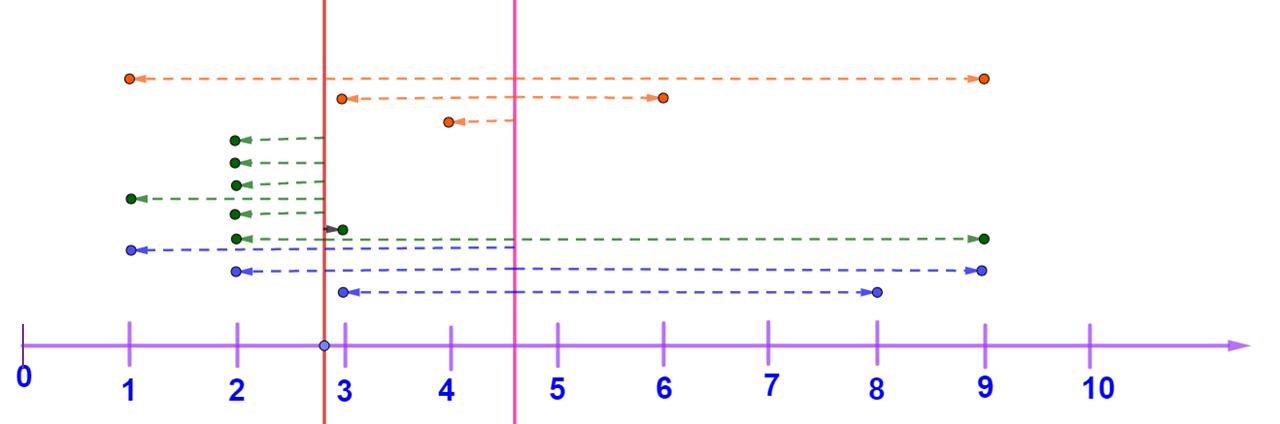
Puedes observar que tomando como referencia la media aritmética del segundo conjunto de datos que es de 2.875, éstos están menos dispersos que los dos anteriores.
Entonces, si te dieran a elegir ordenar algunas de las habitaciones ¿cuál elegirías? Tal vez elegirías el tercer conjunto de datos por estar menos dispersos y tener menos “juguetes” que recolectar.
Otra elección válida podría ser el segundo conjunto ya que, aunque son más elementos, se encuentran menos dispersos.
En el contexto de los juguetes regados, es muy probable que se elija el que tenga menos dispersión. Ahora, analiza con cuidado el nuevo contexto que se le dará a los mismos conjuntos de datos.
Contexto 2
Tres agencias de atención telefónica tienen empleados que trabajan 2 horas en distintos horarios.
La primera agencia cuenta con 5 empleados, de los cuales, uno inicia su trabajo a la 1 de la tarde, otro a las 2 de la tarde, otro a las 3 de la tarde, otro a las 8 de la noche y otro a las 9 de la noche.
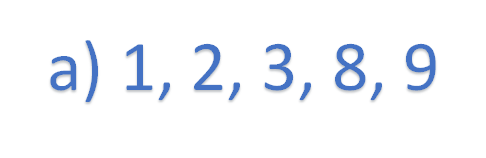
La segunda agencia cuenta con 8 empleados, de los cuales uno comienza a trabajar a la 1 de la tarde, cinco a las 2 de la tarde, uno a las 3 de la tarde y el último a las 9 de la noche.
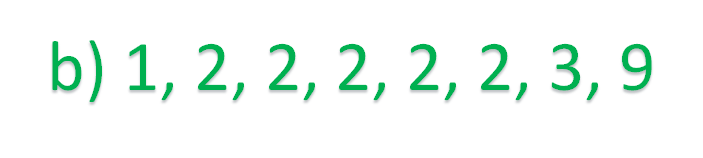
La tercera agencia cuenta con 5 empleados; de los cuales, uno comienza a trabajar a la 1 de la tarde, otro a las 3 de la tarde, otro a las 4 de la tarde, otro a las 6 de la tarde y el último a las 9 de la noche.
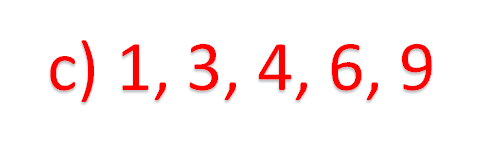
Como puedes observar, los datos son los mismos, pero ahora el contexto cambió, no se trata de recolectar juguetes. Ahora se trata de los horarios de atención de tres empresas. ¿A qué agencia elegirías?
Es probable que la segunda opción, ahora no sea la mejor elección, ya que no tiene mucha variedad en sus horarios, en cambio puede que la mejor opción sea la empresa del inciso “c”, porque tiene más variedad en sus horarios de atención.
Ahora, realiza la siguiente actividad:
Anota 2 contextos distintos para los tres conjuntos de datos, como se realizó con la situación anterior. En un contexto deberá convenir elegir el que tenga sus datos menos dispersos, y en el otro deberá convenir elegir el que tenga sus datos más dispersos. No puedes repetir los contextos que ya se trabajaron en esta sesión.
Después de esta actividad, analiza otros conjuntos de datos.
Para el conjunto 1, los datos que lo integran son:

Para el conjunto 2, los datos son:

Y para el conjunto 3, los datos que lo forman son:

Calcula la media aritmética, la mediana, la moda y el rango de los tres conjuntos anteriores.
Para el conjunto 1, la media aritmética es igual a la suma de 1 más 2 más 8 más 10, entre el total de datos, es decir, entre 4. Que es igual a 21 entre 4, lo que resulta 5.25.

Al ser 4 datos, para determinar la mediana se consideran los dos valores centrales al estar ordenados, ellos son el 2 y el 8, y al calcular el promedio de ellos, es decir, 2 más 8, entre 2, el resultado es 10 entre 2, que es 5.

No tiene moda, ya que no hay algún dato que tenga mayor frecuencia. Por último, el rango es igual a la diferencia del dato mayor, menos el menor, es decir, 10 menos 1, que es igual a 9.
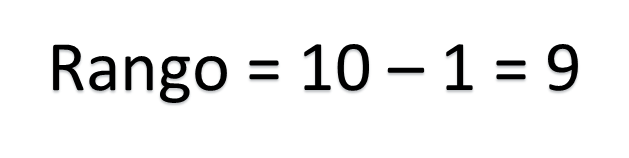
Por lo tanto, para el conjunto 1, las medidas quedan de la siguiente manera:
Media = 5.25
Mediana = 5
Moda = no tiene
Rango = 9
Para el conjunto 2, la media aritmética es igual a la suma de 1 más 3 más 7 más 10, entre el total de datos, es decir, entre 4. Que es igual a 21 entre 4, da como resultado 5.25.
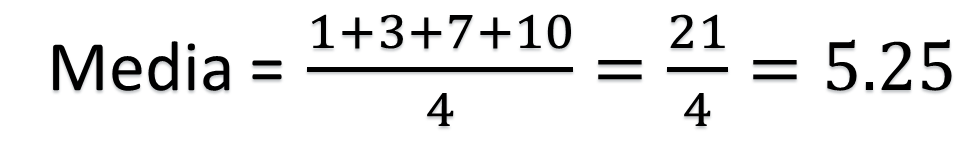
Para calcular la mediana y al ser cuatro datos, se consideran los dos centrales cuando se encuentran ordenados; en este caso son el 3 y el 7, por lo cual se debe obtener el promedio de ellos, es decir, 3 más 7, entre 2. La suma es 10 que al dividirse entre 2 resulta 5.
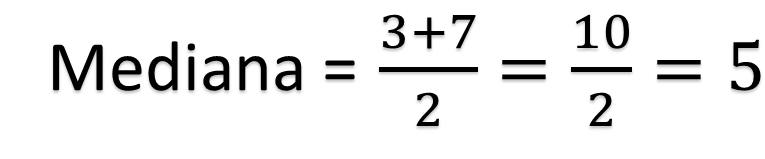
No tiene moda, ya que ningún dato tiene una frecuencia mayor que los demás. El rango es la diferencia entre el dato mayor y el menor, es decir, 10 menos 1, resulta ser igual a 9.
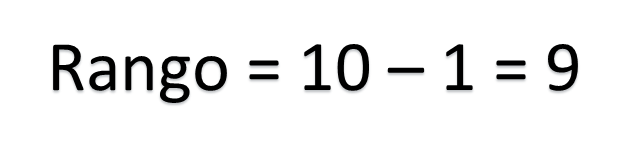
Por lo tanto, para el conjunto 2, las medidas quedan de la siguiente manera:
Media = 5.25
Mediana = 5
Moda = no tiene
Rango = 9
Finalmente, para el conjunto 3, la media aritmética se obtiene mediante la suma de 1 más 4 más 6 más 10, entre 4. Que es igual a 21 entre 4, de donde se obtiene el resultado de 5.25.
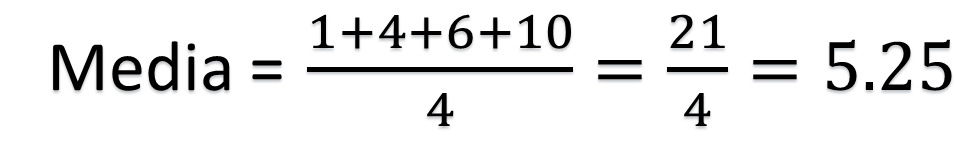
Al igual que en los conjuntos anteriores, se tienen cuatro datos, por lo que mediana es el promedio de los dos centrales cuando se encuentran ordenados. Así, la mediana es igual al promedio de 4 y 6. Por ello, se suma 4 más 6, y se divide esta suma entre 2; el resultado es 10 entre 2 que es igual a 5.
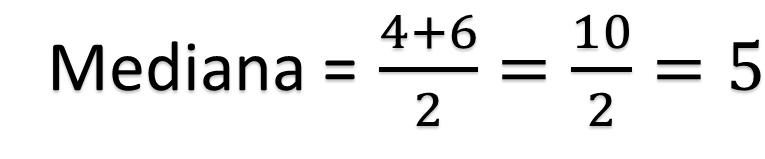
Dado que todos los datos tienen igual frecuencia, este conjunto no tiene moda. Por último, el rango de este conjunto es 9 debido a que es la diferencia del dato mayor menos el menor, es decir, 10 menos 1, que es igual a 9.
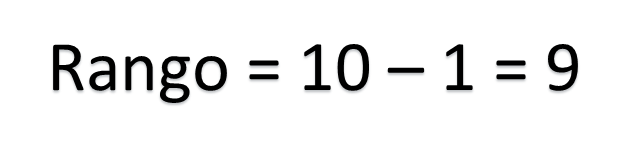
Por lo tanto, para el conjunto 3, las medidas quedan de la siguiente manera:
Media = 5.25
Mediana = 5
Moda = no tiene
Rango = 9
Puedes observar que, para los tres conjuntos, aunque tienen algunos datos distintos, coinciden en la media, la mediana, la moda y el rango.
¿Este nivel de análisis serviría para describir el comportamiento de cada conjunto?, ¿o para tomar alguna decisión?
Dado que las medidas anteriores son iguales para los tres conjuntos, ahora observarás qué tan dispersos están los datos. Para ello, distribuye cada conjunto de puntos en una recta numérica.
En la siguiente recta se muestran los puntos de color azul que corresponden a los datos del conjunto 1, los puntos de color verde que son los datos del conjunto 2 y los puntos de color rojo correspondientes a los datos del conjunto 3.
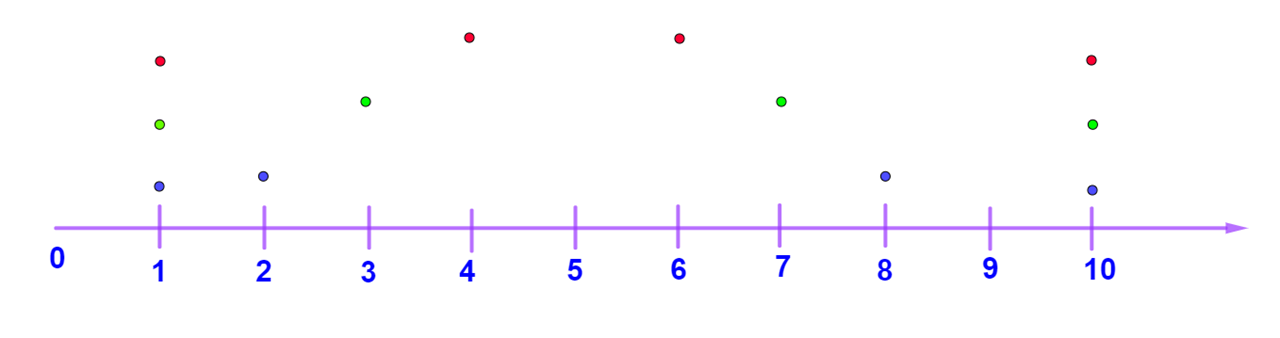
¿Se puede determinar con esta recta, cuáles están más dispersos y cuáles menos dispersos?
Se podría decir que sí, pero es necesario tener presente que falta un elemento de referencia para determinar qué tan alejados están los puntos de ésta.
¿Cuál es ese elemento de referencia que hace falta para hacer el análisis? La media aritmética, la cual, según los cálculos, es 5.25 en todos los casos. Así que agrégala al esquema, como una línea perpendicular a la recta numérica.
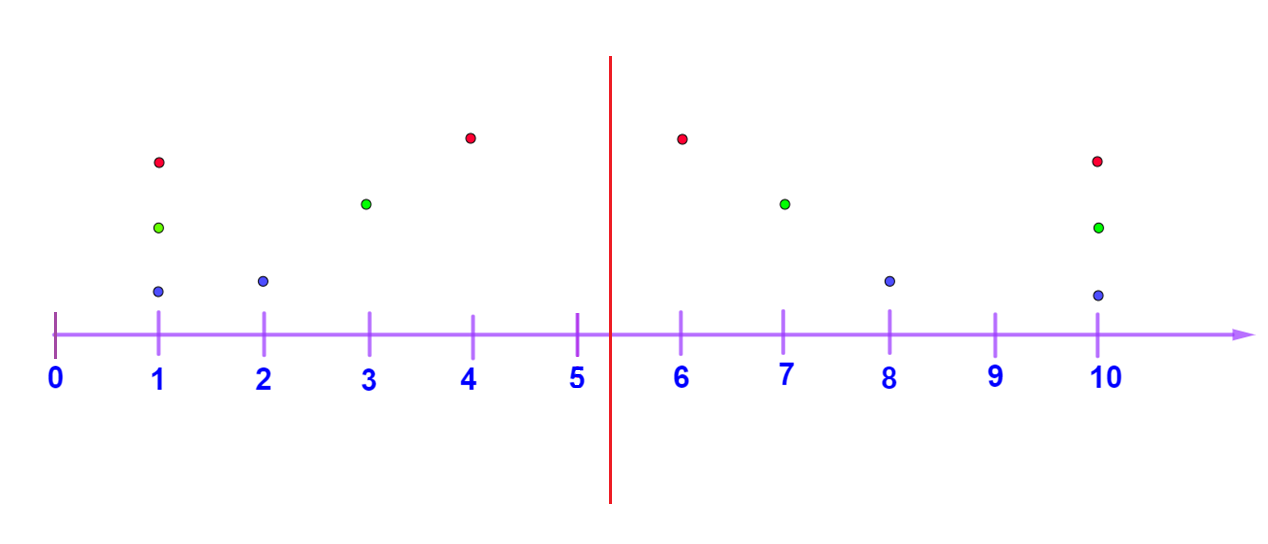
Teniendo a la media aritmética como referencia, ¿ya se puede visualizar en el esquema qué conjunto de datos está más disperso y qué conjunto está menos disperso?
Seguramente ya identificaste de manera más clara esta diferencia. Ahora, apoya el análisis trazando líneas auxiliares que representarán las distancias de cada uno de los puntos a la media. Observa la siguiente imagen.
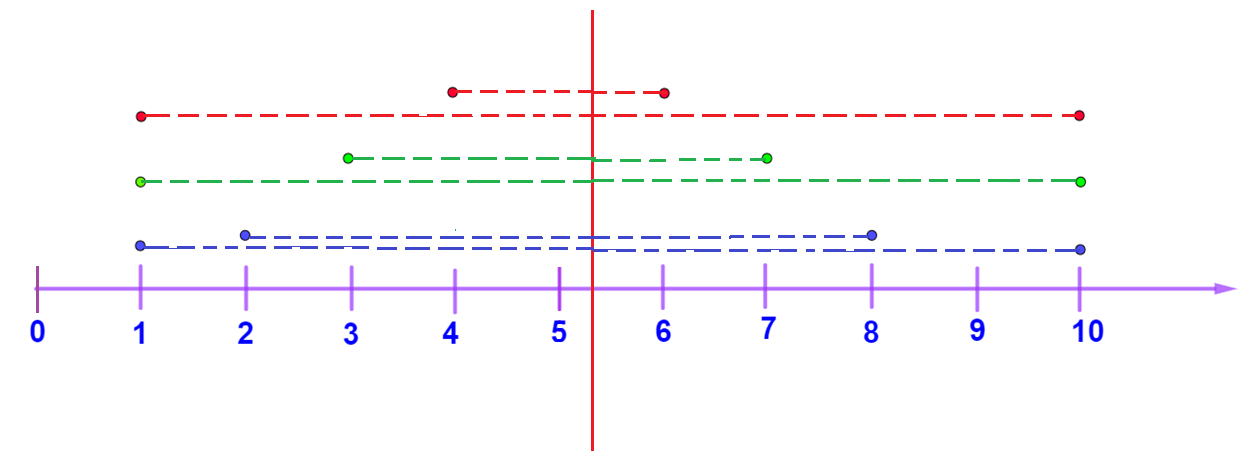
Trazando estos segmentos auxiliares se hace más evidente cada una de las diferencias. En ellos se observa que los datos del conjunto azul están más dispersos, los datos del conjunto verde están menos dispersos que los datos del conjunto azul y, por último, los datos del conjunto rojo están menos dispersos que los datos del conjunto verde.
No siempre se tiene la posibilidad de ubicar los datos en un segmento de recta, en esos casos se puede usar una tabla para representar la información. Observa cómo.
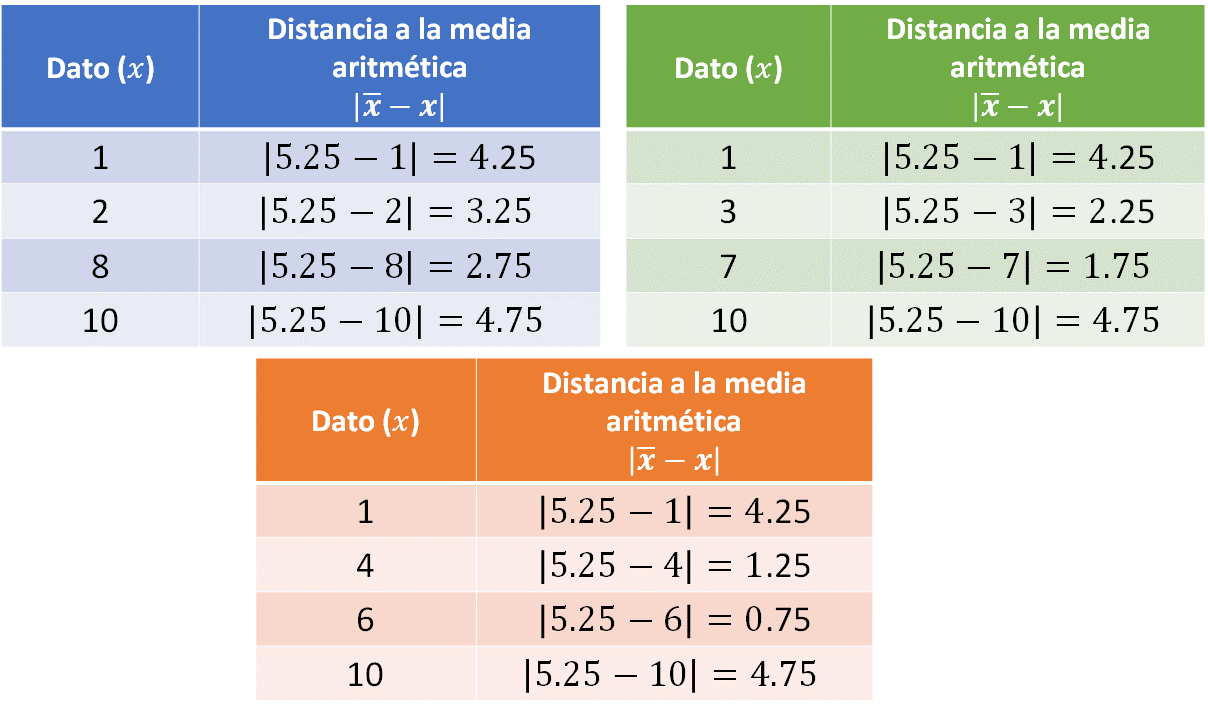
- Para el conjunto 1, se colocan en la primera columna los datos del conjunto y en la segunda columna se calcula la distancia mediante el valor absoluto de la diferencia de la media menos el dato.
- En la segunda fila se encuentra el primer dato del conjunto, es decir, el 1 y posteriormente el valor absoluto de la diferencia de la media menos el dato, es decir, el valor absoluto de 5.25 menos 1 que es igual a 4.25.
- En la tercera fila se encuentra el segundo dato del conjunto, es decir, el 2 y luego, el valor absoluto de la diferencia de la media menos el dato, es decir, el valor absoluto de 5.25 menos 2 que es igual a 3.25.
- En la cuarta fila se ubica el tercer dato del conjunto, que es 8, y posteriormente el valor absoluto de la diferencia de la media menos el dato, que en este caso es 5.25 menos 8 que es igual a 2.75 negativo, cuyo valor absoluto es 2.75.
- Por último, para el cuarto dato del conjunto, es decir, el 10 se determina el valor absoluto de la diferencia de la media menos el dato, por lo que se tiene, el valor absoluto de 5.25 menos 10 que es igual a 4.75.
La tabla para el conjunto 1 queda de la siguiente manera:

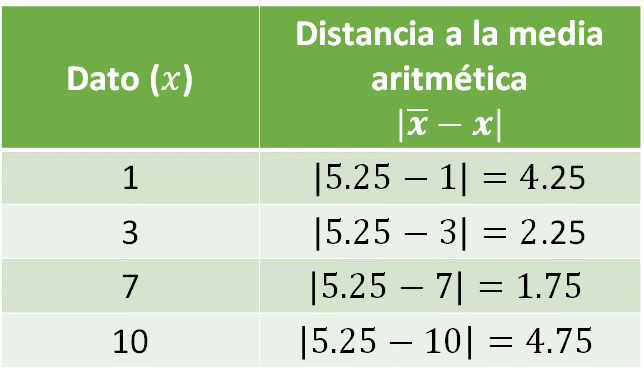
Realiza el mismo procedimiento para el conjunto 2.
- Para el primer dato, que es 1, se tiene el valor absoluto de la diferencia de la media menos el dato, es decir, el valor absoluto de 5.25 menos 1 que es igual a 4.25.
- Para el segundo dato, es decir, 3, se tiene el valor absoluto de la diferencia de la media menos el dato, es decir, el valor absoluto de 5.25 menos 3 que es igual a 2.25.
- En el caso del tercer dato, el valor absoluto de la diferencia de la media menos el dato, es decir, el valor absoluto de 5.25 menos 7 que es igual a 1.75.
- Por último, se encuentra el cuarto dato de este conjunto, es decir, el 10. Para este caso se determina el valor absoluto de la diferencia de la media menos el dato, es decir, el valor absoluto de 5.25 menos 10 que es igual a 4.75.
La segunda tabla queda de la siguiente manera:
Realiza el mismo procedimiento para el conjunto 3.
- En la fila del primer dato también se encuentra el valor absoluto de la diferencia de la media menos el dato, es decir, el valor absoluto de 5.25 menos 1, que es igual a 4.25.
- Para el segundo dato, es decir, el 4, el valor absoluto de la diferencia de la media menos el dato es, el valor absoluto de 5.25 menos 4, que es igual a 1.25.
- En la siguiente fila se encuentra el tercer dato del conjunto, es decir, el 6, y posteriormente el valor absoluto de la diferencia de la media menos el dato, o sea, el valor absoluto de 5.25 menos 6, que es 0.75.
- Por último, se encuentra el cuarto dato, el 10, así como el valor absoluto de la diferencia de la media menos el dato, de donde se obtiene el valor absoluto de 5.25 menos 10, que es igual a 4.75.
La última tabla queda de la siguiente manera:

Comparando las tablas de los tres conjuntos de datos es posible realizar el análisis de la dispersión de los datos. En este caso, se observa que los datos del conjunto 3, que corresponden a la tabla anaranjada, se encuentran más cerca de la media aritmética.
¿Cómo se puede asegurar qué conjunto de datos tiene una menor dispersión con estos valores absolutos? El análisis de la dispersión de los datos de un conjunto es la base para comprender la desviación media, que es el tema que abordarás en la siguiente sesión.
Con esto, has concluido la sesión. Recuerda que éste es un material de apoyo y, para complementar lo estudiado, puedes consultar otras fuentes como tu libro de texto de matemáticas de segundo grado.
El reto de hoy:
Resuelve algunos de los problemas o ejercicios sobre las medidas de tendencia central. Para ello, consulta tu libro de texto de Matemáticas de segundo grado.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas