Resolver problemas de cálculo de perímetro y área del circulo

Resolver problemas de cálculo de perímetro y área del circulo

Aprendizaje esperado: calcula el perímetro y el área de polígonos regulares y del círculo a partir de diferentes datos.

Énfasis: calcular el perímetro y el área del círculo a partir de diferentes datos.

¿Qué vamos a aprender?

En esta sesión aprenderás a resolver problemas en los que se requiere calcular el perímetro y área de un círculo.

¿Qué hacemos?

Para iniciar, lee las siguientes preguntas:

• ¿Cómo calcular el perímetro y área de un círculo?
• ¿Sabes cuál es la diferencia entre círculo y circunferencia?

Para saberlo, analiza detalladamente toda la información del siguiente problema, y anota en tu cuaderno tus dudas y hallazgos.

Marta necesita saber la medida de la superficie de una mesa circular para comprar un mantel. ¿Qué puede hacer Martha para conocer la medida de la superficie y así poder comprar el mantel?

Los hijos de Marta: Manuel, María y Paco le propusieron diferentes alternativas de solución.

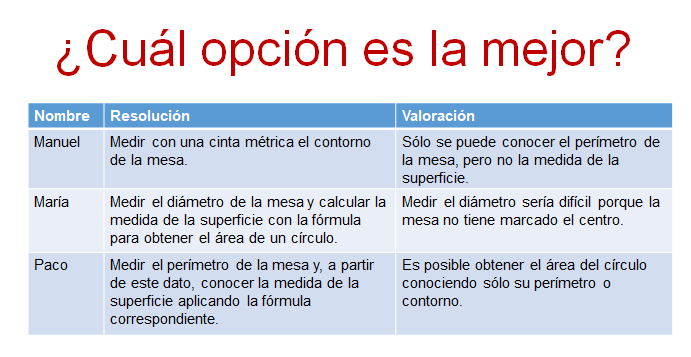
• Manuel propuso medir con una cinta métrica el contorno de la mesa y dar al vendedor de telas, únicamente, la cantidad que resulta de esa medición.
• María dijo que era mejor medir con un metro el diámetro de la mesa y, a partir de ahí, calcular la medida de la superficie con la fórmula para obtener el área de un círculo.
• Paco, que es el hermano mayor, mencionó que lo mejor sería medir el perímetro de la mesa, para, a partir de ahí, conocer la medida de la superficie aplicando la fórmula correspondiente.

¿Quién piensas que tiene razón? Valora las 3 opciones que se presentan para resolver el problema.

La primera no es la opción adecuada, porque de esta manera sólo se puede conocer el perímetro de la mesa, pero no la medida de la superficie. Con esta medida, el tendero puede ofrecer un trozo de tela, con el que se podrá rodear el contorno de la mesa, pero no cubrir su superficie adecuadamente.

La segunda opción podría ser buena, pero hay un inconveniente. Ya que, si la mesa no tiene marcado su centro, sería difícil trazar el diámetro. Probablemente, se obtendría una mala aproximación del área.

En cambio, la tercera opción, aunque es más complicada, es mejor matemáticamente ya que es posible obtener el área del círculo conociendo sólo su perímetro o contorno.

Pero, para comprender cabalmente esta opción, es necesario conocer conceptos y procedimientos acerca del área y perímetro del círculo.

Empieza por conocer la diferencia entre el círculo y la circunferencia. ¿Existen diferencias?

Sí, existen diferencias, pero también tienen elementos en común, por ejemplo: el punto llamado centro y el segmento de recta que se conoce como radio. De hecho, es a partir de estos elementos que se puede definir el círculo y la circunferencia.

Se llama circunferencia a todos los puntos del plano que se encuentran a la misma distancia de un punto fijo en el mismo plano. A ese punto fijo se le nombra como centro de la circunferencia. La sucesión continua de puntos que conforman la circunferencia forman una curva. En la figura está trazada en color rojo. El radio es cualquier segmento de recta que va del punto central a la circunferencia, suele simbolizarse con la letra “r” y en la imagen está marcado con color verde.

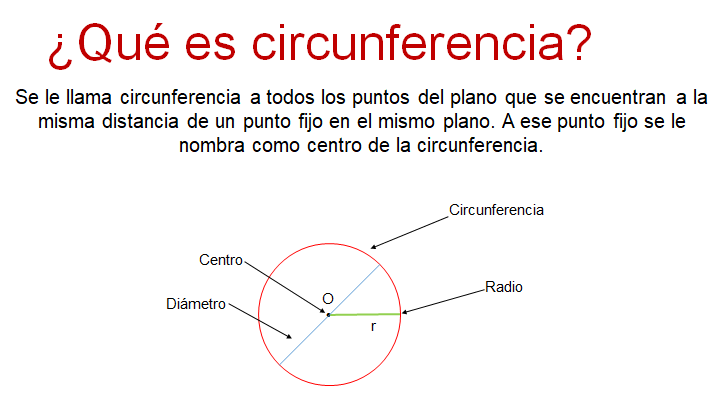
Como se observa, el diámetro es el segmento de recta que pasa por el centro de la circunferencia y toca dos de puntos opuestos a ella.

Una vez que comprendiste qué es la circunferencia, es más fácil entender qué es el círculo. El círculo comprende todos los puntos de la circunferencia y todos los puntos que están en el interior, es decir, se compone tanto de la circunferencia como de la superficie que está en su interior. El círculo de la siguiente imagen está integrado tanto de la curva en color rojo como de la superficie azul.

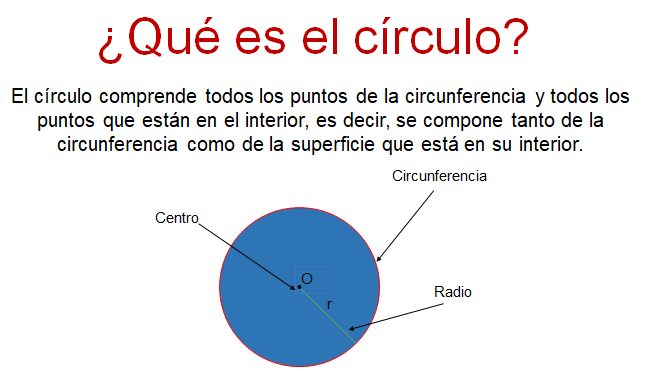
Como se observa, la circunferencia es el borde del círculo. En otras palabras, la circunferencia es el perímetro del círculo. Por ello es preciso explicar que la longitud de la circunferencia se mide en unidades lineales y la superficie del círculo se mide en unidades cuadradas.

No sólo es importante conocer los conceptos de círculo y de circunferencia, porque para resolver problemas, ya sean de la vida real como el problema del mantel u otros que te plantearás en tu vida académica, también es imprescindible conocer las fórmulas para calcular el perímetro y el área de un círculo.

La fórmula para obtener el área del círculo es A igual a pi por r al cuadrado. Donde A mayúscula representa el valor del área del círculo, pi es un número cuyo valor se aproxima a tres punto catorce dieciséis y “r” representa la longitud del radio del círculo.

La fórmula para obtener la longitud de la circunferencia o el perímetro del círculo es C igual a pi por D, donde C representa el perímetro o longitud de la circunferencia, pi ya se comentó que vale aproximadamente 3 punto 14, 16, y D representa la longitud del diámetro del círculo.

Como el diámetro es igual a dos radios, también se puede usar la fórmula: C es igual a pi por dos r o dos pi por r, en donde r representa la medida del radio. Considera que el orden en que aparecen los factores no altera el producto.

Antes de resolver el problema del mantel circular, se van a resolver problemas menos difíciles donde se aplican directamente las fórmulas anteriores.

Por ejemplo:

¿Qué harías para resolver este problema? ¿Qué requieres calcular: el perímetro o el área del campo circular?

Como se trata de cercar un campo circular, se tiene que saber la longitud de la circunferencia o perímetro del círculo, por lo tanto, utiliza la fórmula C es igual a pi por d para saber la medida de la circunferencia del campo. Y ya que conoces que el diámetro mide 12.5 metros y como el valor de pi se aproxima a 3 punto 1416 sustituye estos valores en la fórmula y realiza las operaciones.

Así, sabes que el valor del perímetro o de la circunferencia del terreno es de 39.27 metros, pero como requieres rodear el terreno 5 veces con el alambre, multiplica la cantidad obtenida por 5. Entonces, se sabe que la respuesta al problema es que se requieren en total 196.35 metros de alambre.

Ahora, analiza un problema donde se utilice la fórmula para calcular el área del círculo.

Sin embargo, en este problema se observa que no se puede únicamente sustituir los datos en la fórmula porque no se sabe cuánto mide el radio del pastel.

Conociendo que un diámetro equivale a dos veces el radio o, dicho de otra manera, el radio es la mitad del diámetro, entonces, el radio debe medir 13 centímetros y teniendo este dato ya es posible sustituirlo en la fórmula para calcular el área del círculo.

Al sustituir en la fórmula tienes que el valor del área es igual a 3.1416 por 13 centímetros al cuadrado. Por la jerarquía de las operaciones, primero eleva al cuadrado los 13 centímetros, lo que resulta 169 centímetros cuadrados. Finalmente, multiplica 3.1416 por 169 centímetros cuadrados y obtienes el resultado. Así, se sabe que la bandeja para presentar el pastel debe medir, al menos, 530 punto 9 centímetros cuadrados de superficie, aproximadamente.

¿Consideras que con esta información ya puedes resolver el problema del mantel circular?

Es importante revisar dos conceptos más acerca del círculo y la circunferencia. Analiza la relación que existe entre el diámetro y la circunferencia.

Para ello, vas a suponer que tienes un aro del cual sabes que su diámetro es de 40 centímetros y requieres saber cuál es la longitud de la circunferencia para construir otro igual. Pero, sólo cuentas con una regla graduada y un hilo que no alcanza para medir la circunferencia del aro. Además, has olvidado por un momento la fórmula que relaciona el perímetro con el diámetro. ¿Qué puedes hacer?

Una manera es cortar 40 centímetros de hilo y lo superpones en el aro para ver cuántas veces cabe, Así, te darás cuenta de que cabe tres veces y un poco más. Entonces, multiplica 3 por 40 centímetros resultando 120 centímetros. Luego, mide el pedazo que falta con el hilo y la regla, y te das cuenta de que este pedazo mide 5 punto 6 centímetros y ya resolviste el problema porque 120 centímetros más 5 punto 6 centímetros suman 125 punto 6 centímetros, que es lo que mide la circunferencia del aro.

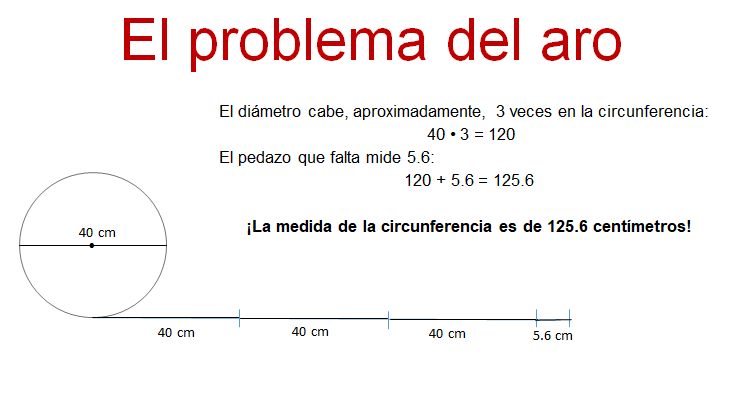
Se sabe que el diámetro cabe en la circunferencia 3 veces y un poco más, pero ¿cuánto es ese poco más? ¿Será posible determinarlo?

Divide la longitud total de la circunferencia: 125.6 centímetros entre 40 centímetros, que mide el diámetro, y eso da por resultado 3.14. Es decir, el diámetro cabe aproximadamente 3.14 veces en la circunferencia. Ésta es una muy buena aproximación de ese cociente. Pero seguramente ya conoces ese número. ¡Sí, es un valor aproximado de pi! El valor del número pi se aproxima a 3.14, lo que quiere decir que pi es la relación que existe entre el diámetro y la circunferencia, e indica que el diámetro de un círculo cabe aproximadamente 3.14 veces en su circunferencia.

Por ello, la fórmula para obtener el perímetro o circunferencia de un círculo es: perímetro igual a pi por D, en donde D representa la longitud del diámetro.

Se te pide que realices este experimento con aros u objetos circulares para verificar en algunos círculos que su diámetro cabe aproximadamente 3.14 veces en su circunferencia.

En los problemas iniciales, se toma el valor de pi como 3 punto 14, 16; esto es correcto porque el valor exacto de pi no está determinado. Entonces, ambos valores: 3 punto 14 y 3 punto 14, 16 se pueden considerar como válidos en los problemas donde se deba utilizar el valor de pi.

Ya has visto por qué la fórmula para calcular la longitud de la circunferencia es C igual a pi por “d”, pero ¿por qué la fórmula para obtener la medida de la superficie es pi por r al cuadrado?, ¿de dónde se obtiene?

Para ello, considera la fórmula para obtener el área de un polígono regular, por ejemplo, del pentágono, que se obtiene dividiendo el valor del perímetro del pentágono por el valor de su apotema entre dos. Esta fórmula se utiliza para obtener el área de cualquier polígono regular, como el decágono que está en la figura del centro, de la siguiente imagen.

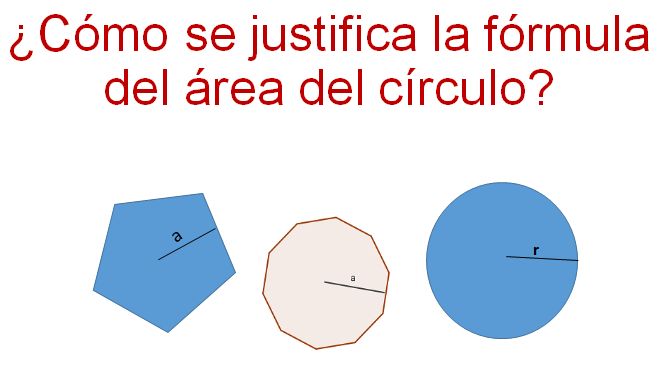
El pentágono tiene cinco lados iguales, el decágono tiene diez lados iguales. Observa las figuras anteriores, e imagina qué pasaría si tuvieras otra con un número de lados mayor a los anteriores por ejemplo 100 lados. ¿Se parecería más al círculo? ¿Verdad que sí?, porque sus lados serían cada vez más de menor medida.

De acuerdo con ello, observa que el perímetro de las figuras se aproxima a la circunferencia del círculo y la apotema se aproxima a la longitud del radio del círculo. Por lo tanto, sustituye en la fórmula del área del polígono la “p” que representa el valor del perímetro por la C que representa la longitud de la circunferencia y la a que representa el valor de la apotema por una r que representa la longitud del radio. De forma abreviada, se obtiene la fórmula: A es igual a C por r entre dos.

Ahora, como se sabe, la longitud de la circunferencia es igual a pi por la longitud del diámetro, entonces para calcular el área A del círculo se multiplica el valor de pi por la longitud del diámetro por el valor del radio, entre 2.

Abreviando, se obtiene la fórmula A igual a pi por d por r entre 2. También se sabe que la longitud del diámetro es igual a dos veces la longitud del radio, o sea D es igual a dos r. Sustituye estas equivalencias en la fórmula y obtienes pi por dos r por r entre 2. Y aplicando la propiedad conmutativa de la multiplicación se tiene que 2 pi por r por r, entre 2.

Si multiplicas r por r, resulta r al cuadrado, y al dividir el número dos en el numerador entre el número dos en el denominador, se obtiene la fórmula que se conoce para calcular el área de un círculo que es área igual a pi por r al cuadrado.

Con lo que has desarrollado hasta aquí, puedes comprender y resolver el problema inicial. Se sabe que Paco tenía la mejor opción para resolver el problema, porque decía que se puede medir la circunferencia y de ahí partir para obtener una muy buena aproximación del área.

La primera opción definitivamente se descarta, porque si se da al vendedor sólo la medida de la circunferencia de la mesa, podría dar un trozo de tela con el que se podría rodear el contorno de la mesa, pero no cubrir su superficie de forma más o menos aproximada.

La segunda es buena resolución, ya que se obtendría la longitud del diámetro y de ahí la del radio, para aplicar la fórmula del área. Sin embargo, las dificultades para realizar la medición del diámetro podrían llevar a un resultado que se alejara mucho de la medida de la superficie del mantel.

Analizando la opción de resolución del problema que propuso Paco. ¿Cómo se hará para que el dato del perímetro de la mesa sea de utilidad para obtener la medida de la superficie? ¿Cuál de los conceptos o relaciones debes utilizar?

Hay que suponer que Marta midió la circunferencia de la mesa y obtuvo 215.7 centímetros.

Como sabes que la longitud de la circunferencia es 3.14 veces la longitud del diámetro, entonces también puedes saber que dividiendo la longitud de la circunferencia entre 3.14 obtendrás la medida del diámetro. Entonces como 215.7 entre 3.14 es aproximadamente 68.7, aseguras que el valor del diámetro de esa mesa circular es aproximadamente 68.7 centímetros.

¿Qué harás a continuación para calcular el área de la mesa circular?

Ya calculaste la medida del diámetro, pero para sustituir en la fórmula del área del círculo debes conocer la medida del radio, ¿cómo puedes obtenerla?

Has visto que el diámetro es dos veces el radio o bien que el radio es la mitad del diámetro, entonces, divide 68 punto 7 centímetros que es la medida del diámetro entre dos y sabrás que, aproximando a las cifras de las décimas, el radio mide 34.3 centímetros.

Al conocer un valor aproximado del radio, ya puedes sustituir los valores en la fórmula del área del círculo que es a igual a pi por r al cuadrado.

Sustituyendo en la fórmula obtienes área igual a 3.14 por 34.3 centímetros al cuadrado. El cuadrado de 34.3 centímetros es 1176.5 centímetros cuadrados (aproximando el resultado a la cifra de las décimas), y esto multiplicado por 3.14 resulta aproximadamente 3694.2 centímetros cuadrados.

Ahora, Marta ya sabe que el área de su mesa es aproximadamente de 3 694.2 centímetros cuadrados.

Ahora conoces la superficie de la mesa circular, que es 3 694.2 centímetros cuadrados. Sin embargo, Marta se ha percatado de que no es suficiente con conocer el área de la mesa, puesto que quiere que el mantel cuelgue 20 centímetros. ¿Qué tiene que hacer ahora Marta? ¿Tú qué harías?

Como el mantel es circular, para que el mantel cuelgue 20 centímetros se puede incrementar 20 centímetros al radio que sabes que mide 34.3 centímetros, es decir, la longitud del radio será de 54.3 centímetros.

Entonces, ¿cuánto deberá medir el área del mantel? Aplica nuevamente la fórmula para obtener el área de un círculo que en este caso ya no es la superficie de la mesa sino del mantel.

Se utiliza la fórmula: área igual a pi por r al cuadrado. Sustituyendo los valores en la fórmula tienes que área es igual a 3.14 por 54.3 centímetros al cuadrado. Realizando las operaciones tienes que 54.3 centímetros al cuadrado es igual a 2 948 punto 49 centímetros cuadrados. Multiplicando esta cantidad por 3.14 resulta aproximadamente 9 258.26 centímetros cuadrados.

El mantel que Marta necesita comprar debe tener un área de 9 258.26 centímetros cuadrados.

¡Marta por fin sabe la medida para comprar su mantel! Le comentó a Paco que quiere ponerle listón alrededor.

¿Qué podría hacer Marta para saber la cantidad de listón necesario?

Has una estimación de la cantidad necesaria de listón que necesita Marta. ¿Serán 2 metros? ¿Más o menos de 2 metros? ¿Serán más o menos de 3 metros? ¿Serán más o menos de 4 metros? ¿Serán más de 5 metros? Registra tu estimación en tu cuaderno.

A Paco le gustan mucho las matemáticas. Por eso se puso el reto de calcular cuánto mediría el listón que compraría su mamá, sabiendo simplemente que el mantel tenía 9258.26 centímetros cuadrados de área. ¿Se podrá saber la longitud de la circunferencia del mantel circular si sólo conoces el área? ¿Tú qué harías?

Lo que hizo Paco fue lo siguiente:

Utilizó la fórmula para calcular el área de un círculo, o sea “A” es igual a pi por radio al cuadrado. Se dio cuenta de que tenía dos datos: el área y el valor del número pi, así que los sustituyó en la fórmula obteniendo 9258.26 centímetros cuadrados es igual a 3.14 por r al cuadrado.

Despejó el radio de esta expresión, primero usó la propiedad simétrica de la igualdad quedando 3.14 “r” al cuadrado igual a 9258.26 centímetros cuadrados. Luego, aplicó la propiedad uniforme dividiendo ambas partes de la igualdad entre 3 punto 14, de manera que obtiene “r” al cuadrado es igual a 9258.26 centímetros cuadrados entre 3.14.

Posteriormente, calculó el cociente anterior, por lo que obtiene que r al cuadrado es igual a 2948.49 centímetros cuadrados (aproximadamente). Finalmente, aplicó la raíz cuadrada de ambos términos de la igualdad, quedando que “r” tiene un valor de 54.3 centímetros.

De esta manera, a partir de conocer el área del mantel circular, Paco calculó la medida, muy aproximada, del radio.

Se sabe que el radio es la mitad de un diámetro, es decir que el diámetro es el doble que el radio, y, por lo tanto, si el radio mide 54 punto 3 centímetros, entonces el diámetro mide 108 punto 6 centímetros.

Conociendo la medida del diámetro, Paco utilizó la fórmula para obtener la longitud de la circunferencia, es decir, C es igual a pi por D. Luego, sustituyó los valores y obtuvo que la longitud de la circunferencia es igual a 3 punto 14 por 108 punto 6 centímetros. Finalmente, resolvió la multiplicación y obtuvo un valor aproximado de 341 centímetros.

Cuando Paco le comentó a su mamá que ya tenía la medida, ella le dijo que ya había medido el contorno del mantel y que había obtenido 3 metros con 41 centímetros.

Ambos obtuvieron la misma medida porque 341 centímetros equivalen a 3 punto 41 metros. Ahora, regresa a la estimación de la cantidad de listón necesaria. ¿Qué tan razonable fue su estimación?

Luego, Paco le dijo a su mamá que debía comprar un poco más de los 3 punto 41 metros.

¿Por qué habrá dicho esto, Paco a su mamá?

Para calcular el perímetro y el área del círculo a través de la fórmula correspondiente se utiliza el valor de pi. Anteriormente se dijo que el valor de pi es el cociente obtenido al dividir la medida de la circunferencia entre la medida del diámetro de un mismo círculo. Esto hace que ese valor esté determinado por la exactitud con que se obtengan dichas medidas.

Seguramente has utilizado pi igual a 3 punto 14 como también pi igual a 3.1416. Otras aproximaciones al valor de pi son 3 punto 14, 15, 9 y pi igual a 3 punto 14, 15, 92, 65. Incluso, si usas una calculadora científica y le indicas que dé el valor pi, seguramente observarás más cifras decimales que las mostradas aquí.

Pero, ninguno de ellos es el valor exacto de pi. Aunque, entre más cifras decimales se consideren para el valor de pi, los resultados de los cálculos donde se haga uso de él, tendrás una mejor aproximación.

Por eso, Paco dijo que 3.41 metros es una cantidad aproximada del listón que debe comprar para colocar alrededor del mantel circular. Él le dijo que debía comprar un poco más de 3 punto 41 metros de listón.

Has llegado al final de la sesión.

El reto de hoy:

No olvides elaborar tus apuntes con las ideas más relevantes de este tema.

Recuerda enriquecer tu conocimiento sobre este tema, consultando en otras fuentes, como tus libros de texto, páginas electrónicas o enciclopedias.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/