Notación científica I
Notación científica I
Aprendizaje esperado: resuelve problemas de potencias con exponente entero y aproxima raíces cuadradas.
Énfasis: resolver problemas de potencias con exponente entero y aproximar raíces cuadradas.
¿Qué vamos a aprender?
Continuarás con el estudio de potencias con exponente entero y aproximarás raíces cuadradas.
En esta sesión, te concentrarás en el estudio en potencias de base 10. Para ello, registrarás tus ideas y conocimientos sobre las potencias de base, para validar o fortalecer esos y otros saberes.
¿Qué hacemos?
Para iniciar, reflexiona en las siguientes preguntas:
¿Alguna vez has reflexionado sobre la curiosidad?
¿Has llegado a pensar que la curiosidad es un motor importante para conocer el mundo que nos rodea?
¿Te asombras cuando encuentras respuestas a tus preguntas?
Grandes pensadoras y pensadores han dedicado mucho tiempo y esfuerzo para entender el mundo, esa es la finalidad de las Matemáticas. La curiosidad, es un motor importante para conocer el mundo que nos rodea, y uno de esos grandes pensadores que se dedicó a entender el mundo, es Arquímedes de Siracusa, quien nació en Siracusa, Sicilia, en el año 287 antes de nuestra era, y murió en la misma ciudad en el año 212 antes de nuestra era.
Arquímedes demostró que toda cantidad, por muy grande que fuera, podía ser calculada. Para difundir ese conocimiento, escribió un libro llamado “Psammites”, en el que responde a la pregunta: ¿cuántos granos de arena son necesarios para llenar todo el universo?
De la información anterior, piensa en lo siguiente:
¿Cuál es la respuesta a la pregunta que se planteó Arquímedes hace muchos siglos?
¿Tendrá respuesta?
Ahora, analiza lo que dos estudiantes de segundo de secundaria encontraron al investigar en libros relacionados con “El Arenario” o “El Contador de Arena”, de Arquímedes.
El alumno 1 encontró la siguiente información:
“Los contemporáneos de Arquímedes pensaban que el número de elementos de un conjunto sólo podía ser expresado hasta un cierto límite. A partir de ahí, las cantidades eran consideradas no calculables”.
¿Estás de acuerdo con la afirmación del párrafo anterior?
¿Qué tan grandes son los números que conoces?
Registra tus respuestas para validarlas o ajustarlas durante el desarrollo de la sesión.
El estudiante 2 encontró la siguiente cita en un libro:
“Arquímedes, después de una serie de cálculos complicados, llegó a la conclusión de que en el universo caben aproximadamente diez a la, sesenta y tres granos de arena”.
¿Puedes saber cuántos granos de arena representa el número que calculó Arquímedes?
¿Qué significado puede tener el número 63?
En la antigua Grecia, los sistemas de numeración no pasaban de 100 millones, sería Arquímedes el primero en traspasar esa barrera en el escrito mencionado antes, conocido como “El Arenario”, que significa contador de arena, en el que pretendía contar todos los granos de arena que contenía el planeta.
Este reto lo hizo con el fin de demostrar que podía numerarse cualquier cantidad por grande que fuera. Se basó en un sistema de tres periodos basados en potencias sucesivas de miríadas: 10 000.
Miríada, es el nombre en griego clásico para el número 10 elevado a la cuarta potencia, igual a 10 000, igual a 100 elevado a la segunda potencia; esto es, cien veces cien. A veces, esta palabra se emplea como adjetivo que denota un número grande o incalculable.
Entre tanto, retoma las preguntas:
¿Puedes saber cuántos granos de arena representan el número que calculó Arquímedes?
¿Qué significado puede tener el número 63?
Una potencia, es la representación abreviada de una multiplicación de factores iguales y que consta de dos partes:
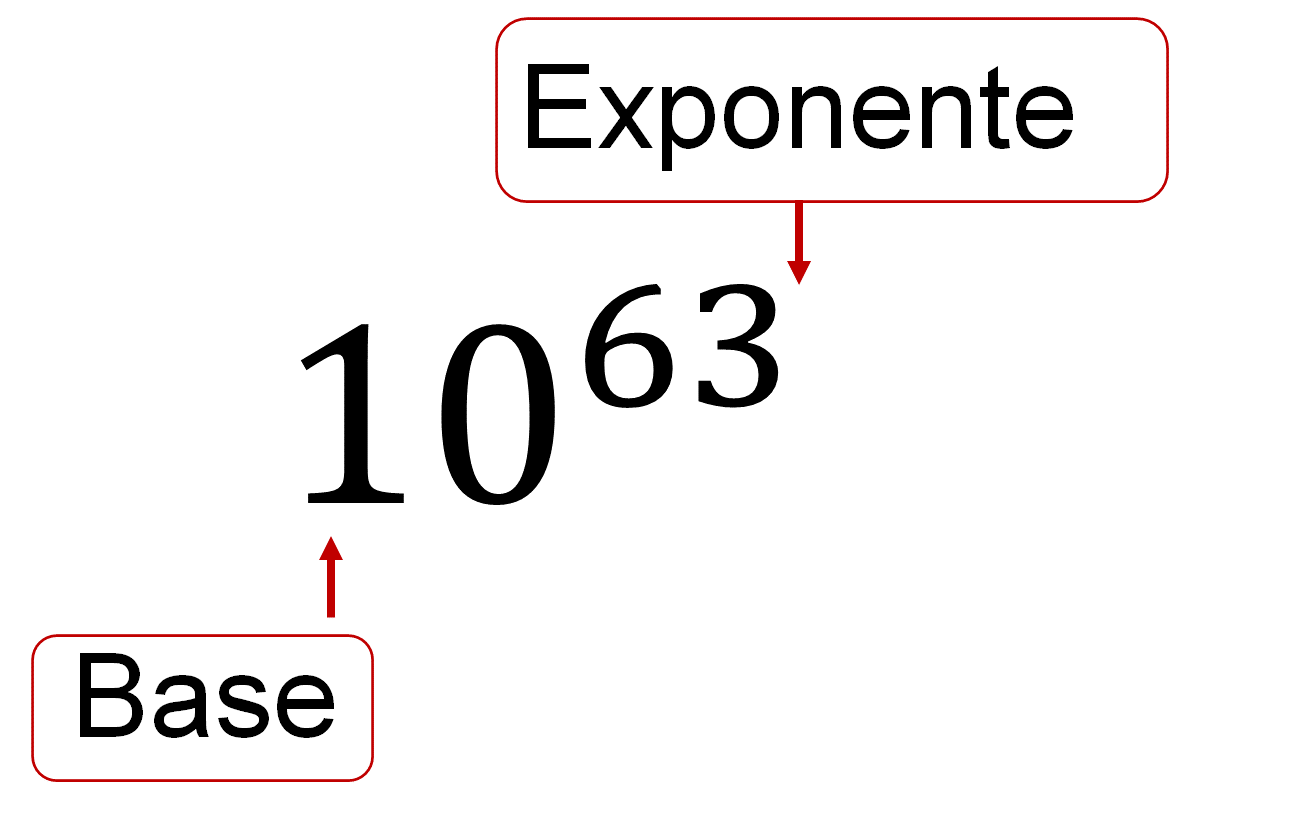
- La base es el número que se multiplica por sí mismo.
- El exponente es el número que indica las veces que se multiplica la base por sí misma.
Bajo esta óptica, el número 63 significa que el número base se multiplica 63 veces por sí mismo, y el producto obtenido es el total de granos de arena. Observa el número.
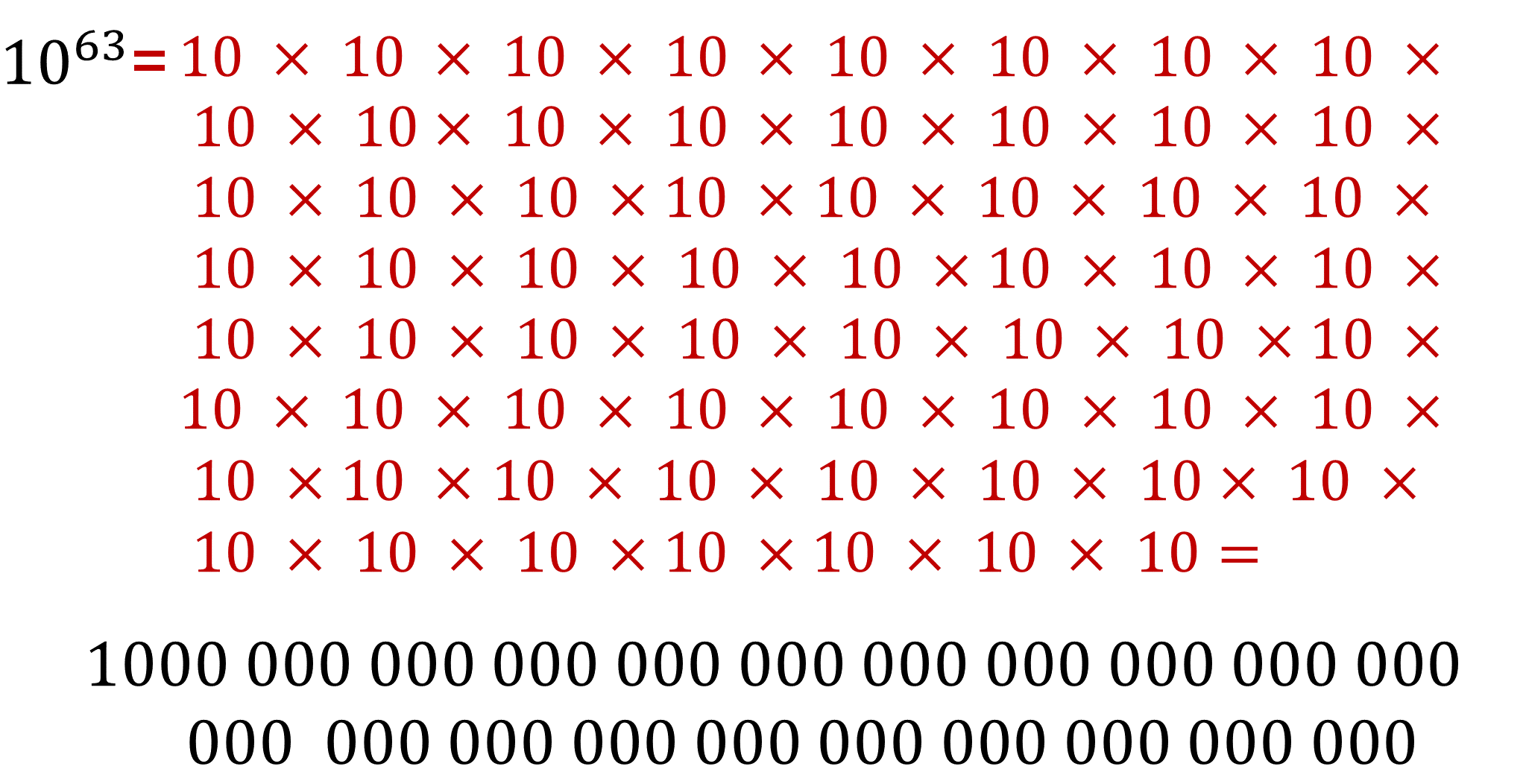
10 elevado a la sexagésima tercera potencia es 10 por 10, por 10… así hasta multiplicarlo 63 veces. El producto de la potencia es un número con 63 ceros. Afortunadamente, en matemáticas se cuenta con la notación científica, que ayuda a representar de manera abreviada cantidades muy grandes o pequeñas.
Para los científicos que estudian fenómenos y objetos de dimensiones muy grandes (como los astros), la notación científica es útil debido a que permite trabajar y operar esos números con cierta facilidad.
En el lenguaje de la ciencia el uso de números muy grandes y pequeños es frecuente. Por ejemplo, para hacer mediciones, como la distancia media aproximada de la Tierra al Sol, se usan números muy grandes, pues ésta mide 150 000 000 kilómetros; o para medir un glóbulo rojo se usan números muy pequeños, pues éste tiene un tamaño de 0.0000075 milímetros.
Para simplificar la escritura de números muy grandes o pequeños se utiliza la notación científica, que es una forma abreviada de representar números mediante una multiplicación de un número, entre 1 y 10, por una potencia de base 10.
En la notación científica, los números se expresan como el producto de dos factores: el primer factor es un número entre 1 y 10, el segundo, una potencia de base 10.
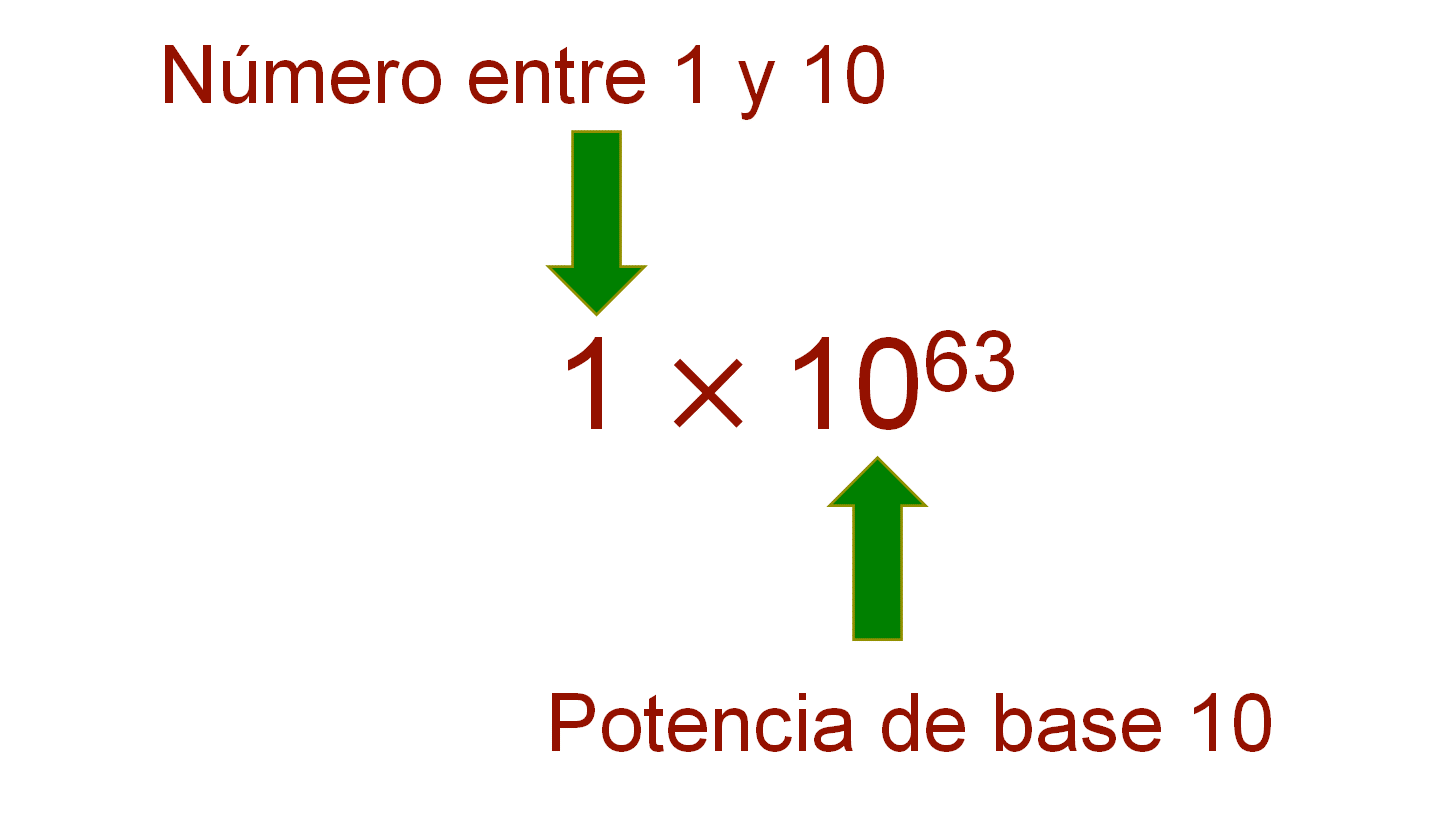
Como puedes ver, en el ejemplo de la cantidad de los granos de arena, el número 1 cumple con las condiciones anteriormente establecidas, ya que es un número decimal entre 1 y 10 que multiplica una potencia de base 10 con exponente 63.
A continuación, si te es posible, usa una calculadora científica y multiplica 1 por 10, por 10, por 10… hasta multiplicar “por 10”, 63 veces.
¿Cuál es el resultado?
El resultado está en notación científica
Ahora, analiza otros ejemplos.
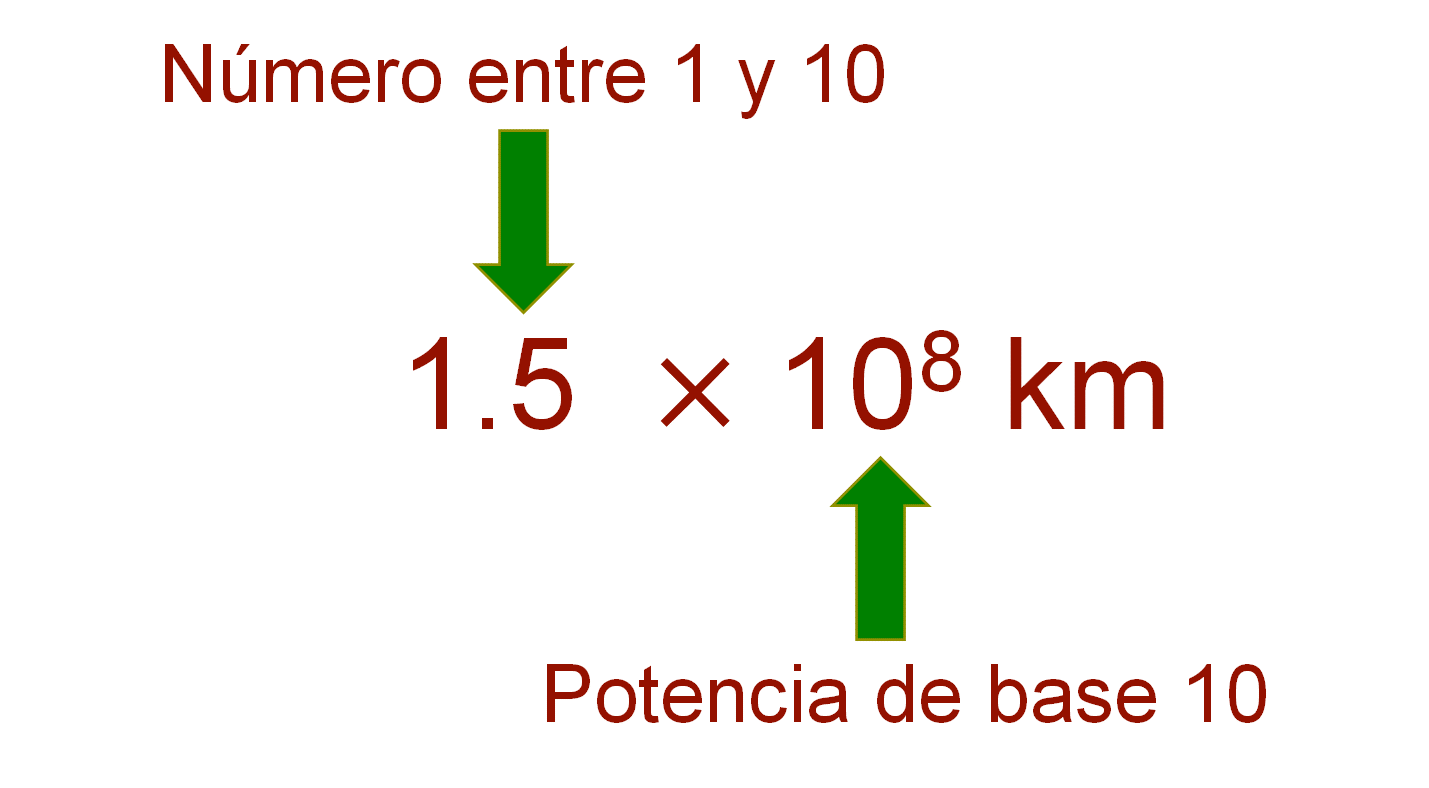
En este segundo caso, el número 1.5 es un número decimal entre 1 y 10, que multiplica una potencia de base 10 con exponente 8. Por lo tanto, cumple con las condiciones de la notación científica.
La distancia de la Tierra al Sol es de 150 millones de km, en notación científica se representa como 1.5 por 10 a la octava potencia. El tamaño de un glóbulo rojo es de 75 diezmillonésimos de milímetro, que se representa en notación científica como 7.5 por 10 a la sexta potencia negativa.

Ahora, conocerás cómo convertir un número, de su expresión común a su expresión en notación científica, y viceversa. Se enfocará esta sesión en la representación de números muy grandes en notación científica, y en otras sesiones lo realizarás con números muy pequeños.
Como sabes, para multiplicar un número decimal por una potencia de 10 se recorre el punto decimal a la derecha tantas posiciones como ceros tenga el número y se agregan ceros cuando es necesario, por ejemplo:

Ahora observa cómo representar un número como potencia positiva de base 10. En estos casos, el número del exponente es equivalente al número de ceros que tiene el número en cuestión.
Por ejemplo:
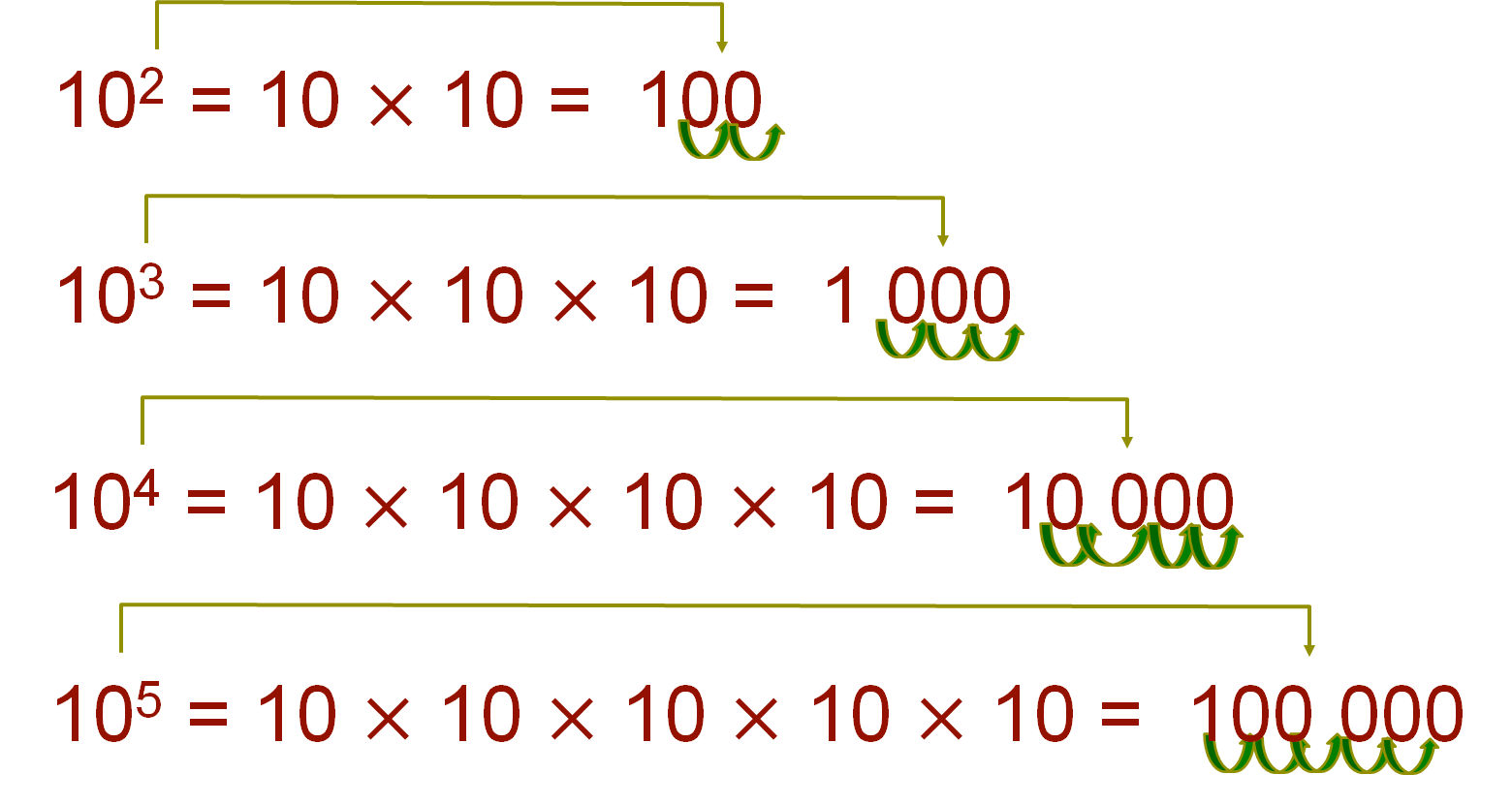
De acuerdo con lo anterior, se puede comprender cómo se convierten números de notación científica a notación decimal. Recuerda tomar nota en tu cuaderno de la información que se genere.
Por ejemplo, en el caso de 2.6 por 10 a la sexta potencia, el exponente indica el número de veces que se multiplica la base, en este caso, el 10, y abreviando, indica el número de ceros que se le agregan al 1; entonces, 10 a la sexta potencia es igual a un millón. Y al multiplicar 2.6 por 10 a la sexta potencia, el punto decimal se recorre seis cifras a la derecha, es decir, el mismo número que representa el exponente. Por lo tanto, 2.6 por 10 a la sexta potencia es igual a 2 600 000.
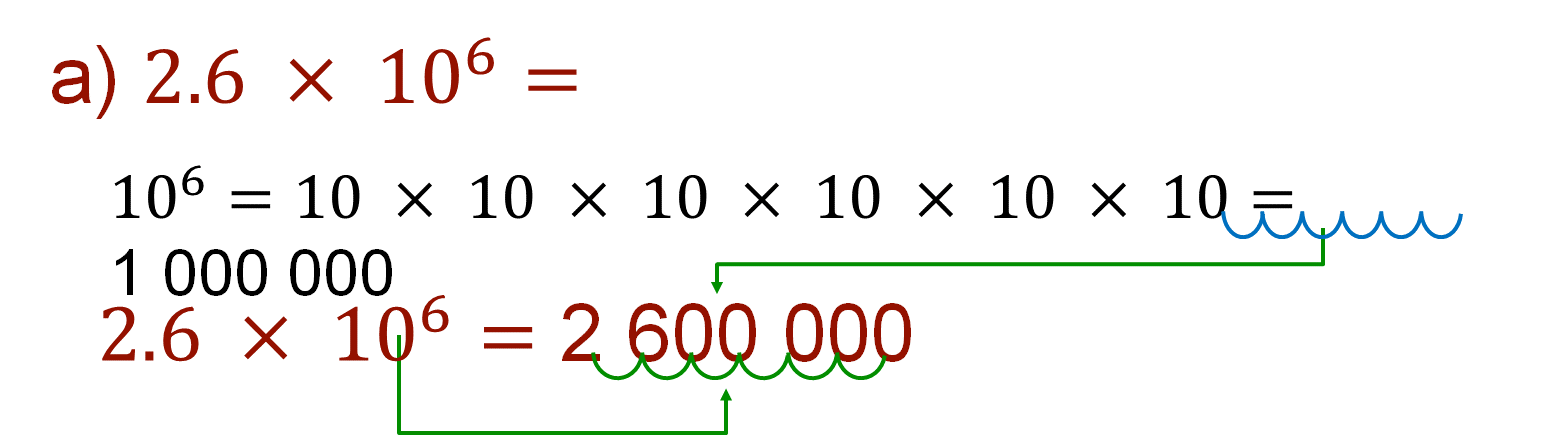
En el segundo ejemplo, 6.35 por 10 a la séptima potencia, al recorrer el punto decimal siete cifras a la derecha y agregando los ceros correspondientes, es igual a 63 500 000.
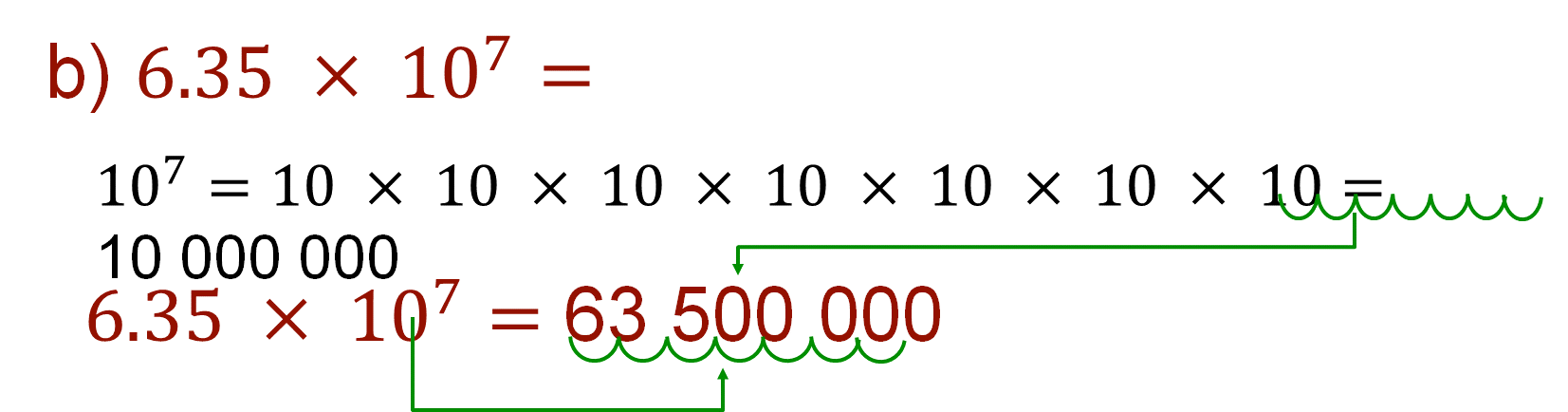
Ahora, identifica cómo pasar de notación decimal a notación científica. En este caso, el punto decimal se recorre a la izquierda las cifras necesarias hasta obtener un número decimal entre 1 y 10, y el exponente de la potencia de base 10 será igual al número de cifras que se haya recorrido el punto decimal. Por ejemplo:
2 600 000, representado en notación científica, es igual a 2.6 por 10 a la sexta potencia, porque el punto decimal se recorrió seis cifras a la izquierda hasta encontrar un número decimal entre 1 y 10.

Y 63 500 000 es igual a 6.35 por 10 a la séptima potencia.
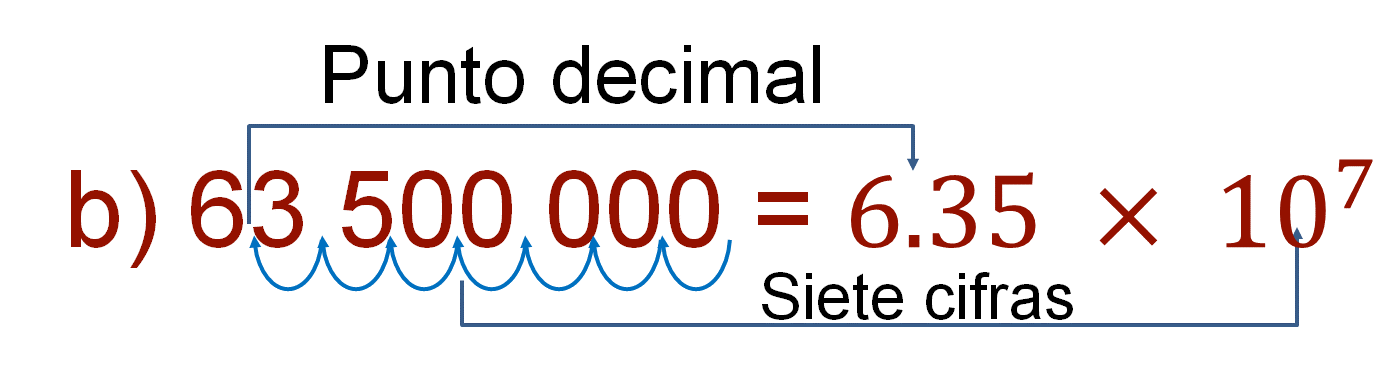
De acuerdo con la explicación anterior, ¿tienes claro cómo representar números en notación científica?
Considera que el número por el que se multiplica la potencia de base 10 obligatoriamente es un número entre 1 y 10; en caso contrario, la representación no sería correcta. Continúa con otros ejemplos.
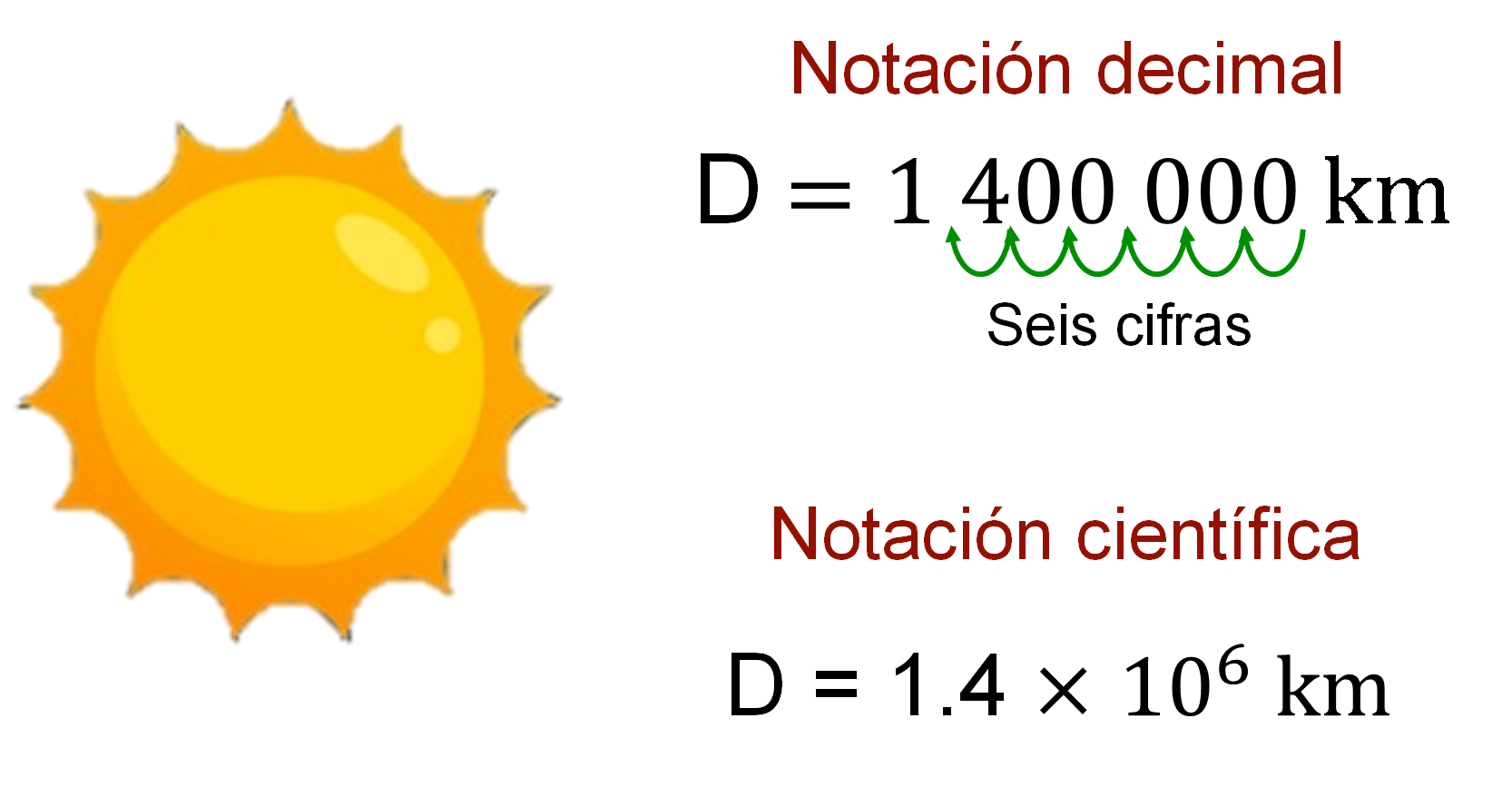
A continuación, escribe en notación científica el diámetro del Sol, que es igual al 1 400 000 km. Considera que el diámetro de una esfera es el segmento que pasa por el centro y tiene sus extremos en la superficie de ésta.
¿Cuál es la representación del diámetro del Sol en notación científica? Presta atención a lo siguiente.
Como el diámetro del Sol es igual a 1 400 000 km, se recorre el punto decimal a la izquierda hasta obtener un número decimal entre 1 y 10, en este caso, es 1.4.
¿Qué representa este valor?
Representa el número por el que se multiplica la potencia de base 10. Y dado que se recorrió el punto decimal seis cifras a la izquierda, el exponente de 10 es 6. Por lo tanto, el diámetro del Sol en notación científica es igual a 1.4 por 10 a la sexta potencia.
Sin duda alguna, la notación científica resulta útil para representar de manera abreviada cantidades muy grandes.
¿En qué otras situaciones piensas que resulta útil utilizar la notación científica?
Para aplicar lo aprendido hasta el momento, realiza la siguiente actividad.
Observa con atención la siguiente tabla y cópiala en tu cuaderno. Posteriormente, trata de completarla. La tabla muestra la distancia media de tres planetas al Sol: Saturno, Urano y Neptuno.
Como puedes observar, la distancia al Sol de Saturno y Neptuno está representada en notación decimal y es de 1,430 millones de km y 4,504 millones de km, respectivamente. Mientras que la de Urano está dada en notación científica y es igual a 2.871 por 10 a la novena potencia.
¿Ya lograste completar la tabla? Ahora, verifica tus respuestas.
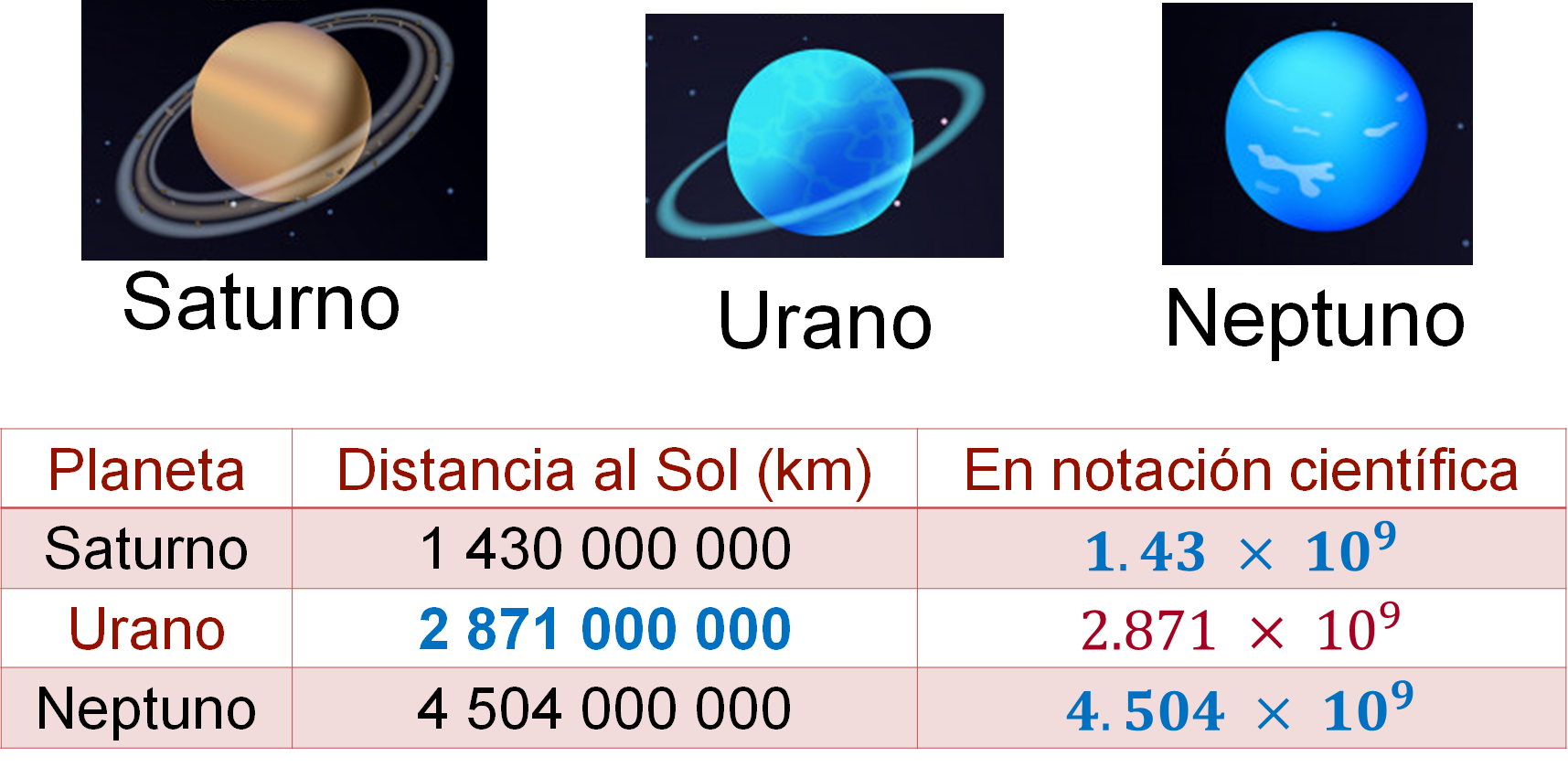
De acuerdo con los datos de la tabla anterior y aplicando lo aprendido, la distancia de Saturno al Sol en notación decimal es igual a mil cuatrocientos treinta millones de km, y en notación científica es 1.43 por 10 a la novena potencia; la distancia de Urano es de 2.871 por 10 a la novena potencia, que en notación decimal es igual a dos mil ochocientos setenta y un, millones de km; y finalmente la distancia de Neptuno al Sol es cuatro mil quinientos cuatro millones, que en notación científica es igual a 4.504 por 10 a la novena potencia.
Ahora, realiza lo siguiente.
Observa la siguiente información, sobre la masa de la Tierra en notación decimal, e identifica cuál de las opciones de respuesta que aparecen a continuación representa la masa de la Tierra en notación científica de manera correcta.
Analiza las opciones:

Ya que hayas seleccionado tu respuesta, arguméntala. Posteriormente, compara tu respuesta con la siguiente información.
La respuesta del inciso “b” no es correcta porque 59.72 no es un número entre 1 y 10, por lo tanto, esa opción se descarta. El número decimal correcto es 5.972, que aparece en los incisos “a” y “c”, ya que éste se encuentra entre 1 y 10. Al contar las cifras que se recorrió el punto decimal, se sabe que son 24 cifras, por lo tanto, la respuesta correcta es el inciso “a”: 5.972 por 10 a la 24 potencia.
Ahora, analiza el siguiente planteamiento.
Se sabe que la distancia que hay entre la Tierra y la galaxia Andrómeda es de 24 trillones de kilómetros, aproximadamente.
¿Cuál es la distancia entre la Tierra y la galaxia Andrómeda expresada en notación científica?
Para responder la pregunta, determina cuántos ceros tiene la cantidad que indica la distancia que hay entre la Tierra y Andrómeda. Después usa una calculadora científica y multiplica 24 por 10, por 10, por 10… tantas veces “por 10” como ceros tenga el número del ejemplo.
¿Cuál es el resultado?
Regístralo para compararlo más delante.
Reflexiona en lo siguiente, considerando el resultado obtenido en la calculadora:
¿El resultado que obtuviste representa el mismo valor que el número 24 trillones?
¿La distancia que hay entre la galaxia Andrómeda y la Tierra se puede escribir también como 24 por diez a la décimo octava potencia?
¿Por qué?
Argumenta si las siguientes expresiones pueden representar al número 24 trillones:
- 0.24 por diez a la vigésima potencia.
- 240 por diez a la décimo séptima potencia.
Una vez que hayas respondido a lo anterior, verifica tus respuestas.
El número 24 trillones tiene 18 ceros. Al multiplicar 24 por 10 dieciocho veces, se obtiene 2.4 por diez a la décimo novena potencia. Ambos valores, 24 trillones y 2.4 por diez a la décimo novena potencia, son los mismos, pues, aunque las representaciones son distintas, tienen el mismo valor, es decir, son representaciones equivalentes.
La distancia que hay entre la galaxia Andrómeda y la Tierra también se puede escribir como 24 por diez a la décimo octava potencia, esto porque esta representación también es equivalente a las anteriores, así como las expresiones 0.24 por diez a la vigésima potencia y 240 por diez a la décimo séptima potencia.
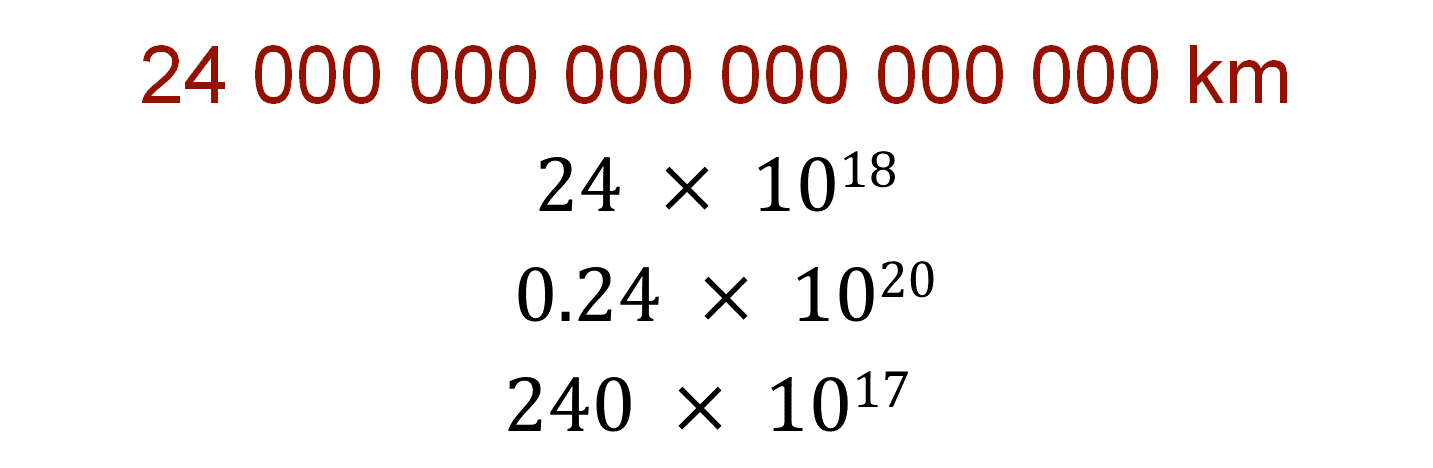
Por lo tanto, las expresiones anteriores son equivalentes, y sólo una de ellas está escrita en notación científica: 2.4 por 10 elevado a la potencia 19, pues 2.4 es un número decimal que está entre 1 y 10, que multiplica una potencia de base 10 con exponente 19.
Continúa con la siguiente situación.
La masa de Mercurio es igual a 330 300 trillones de kg. Un estudiante la representó en notación científica como 330.3 por 10 a la 21, kilogramos.
¿Por qué esta expresión no es correcta?
Porque el primer factor de la representación en notación científica es un número entre 1 y 10, y 330.3 es un número mayor a diez, por lo que no cumple con la condición establecida para la representación como notación decimal.
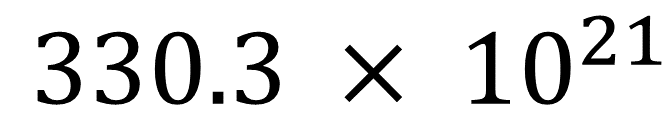
La representación correcta es 3.303, ya que después del punto se escriben todos los números diferentes a cero, y el número de las cifras recorridas, que son 23.

¿Qué representa este valor?
El valor del exponente. El exponente es el número que indica las veces que se multiplica la base por sí misma. La base es el número que se multiplica por sí mismo.
Para continuar con la sesión, reflexiona en la siguiente interrogante:
¿Qué significa el orden de magnitud en la notación científica?
La importancia de analizar el orden de magnitud de números expresados en notación científica es que permite saber qué tan grande es un número comparado con otro.
Por ejemplo:
El orden de magnitud del número 9,700,000,000 es de 10 a la décima potencia porque es un número que está entre diez a la novena potencia y diez a la décima potencia, y es más próximo a este último.
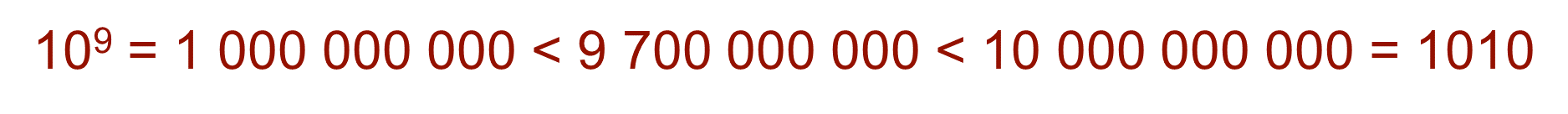
En notación científica:
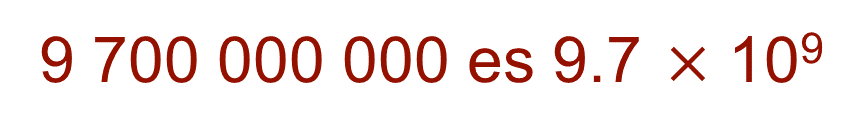
En “a por diez a la “n””, “a” es un número entero o decimal que se llama coeficiente, “n” es un número entero y 10 a la “n” es el orden de magnitud. Para cantidades muy pequeñas, “n” tendrá el signo negativo.
Has concluido esta sesión. Si deseas saber más del tema, puedes consultar tu libro de texto de Matemáticas, de segundo grado.
El reto de hoy:
Compara los siguientes números en notación científica y determina cuál es mayor.
Primer caso. ¿Cuál de estos dos números es mayor?
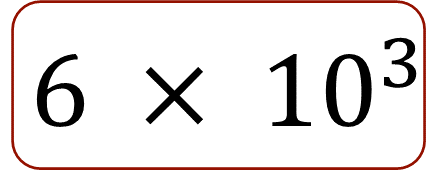
o

Segundo caso. ¿Cuál es mayor?

o
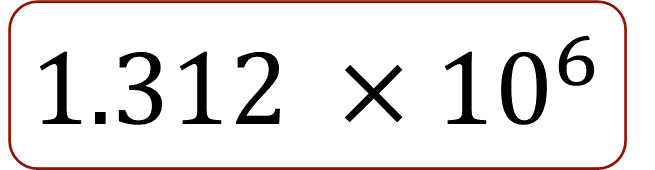
Registra los criterios que empleaste para comparar los números anteriores.
Finalmente, para fortalecer estos conocimientos, resuelve los problemas de potencias que vienen en tu libro de texto, sobre las cantidades expresadas con notación científica.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
