Diseñemos un mosaico
Diseñemos un mosaico
Aprendizaje esperado: uso de fracciones del tipo m/2n (medios, cuartos, octavos, etcétera) para expresar oralmente y por escrito medidas diversas.
Énfasis: identificar las fracciones que resultan de subdividir varias veces un conjunto en la misma proporción o razón.
¿Qué vamos a aprender?
En la sesión de hoy contaras con un dado.
Las caras del dado dicen:
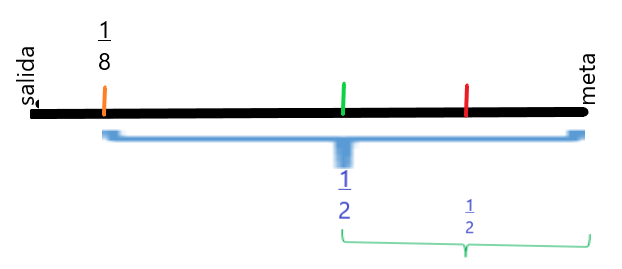
Avanza , avanza o avanza del camino que te falta.
Avanza , avanza o avanza del camino que te falta.
Vamos a Jugar.
¿Qué hacemos?
Si tiras el dado y en el primer tiro te sale el camino lo dividimos en 2 y avanzamos
una sección y en el segundo tiro sale nuevamente no continua con las secciones anteriores, sino que vuelve a dividir lo que resta del camino en 2 partes y avanzaras la mitad.
¿En dónde más podrías usar así las fracciones? mira, aquí tienes 8 pelotas que también te pueden ayudar con una duda. Mira, te voy a dar de ellas, o sea, la mitad, bien, ahora imagina que llegas a tu casa y tu hermano te pide que le regales la mitad de tus pelotas de tenis, es decir entonces tienes que repartir las pelotas de tenis en 2 grupos y darle un grupo a tu hermano y otro grupo sería para ti, muy bien, ahora puedes ver que, aunque le diste de las pelotas de tenis a tu hermano no fueron la misma cantidad con las que tú iniciaste el reparto. y entonces, la mitad de las pelotas que le diste a tu hermano, ¿Qué fracción representa del total que tenía?
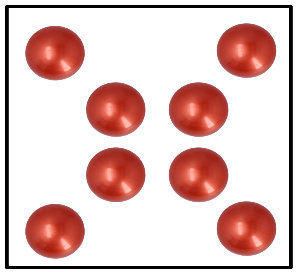
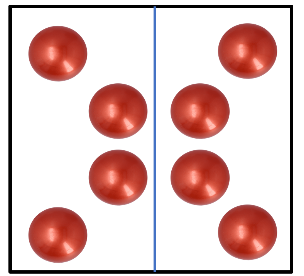
Tenías 8 pelotas y las repartiste en 2 grupos iguales, entonces allí repartiste de las pelotas.
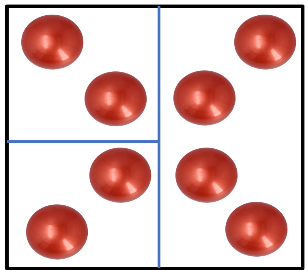
Después repartiste las pelotas de tenis que te dio entre tu hermano y yo, entonces, aunque repartiste las pelotas de tenis entre 3 personas, en realidad no fueron tercios, porque tenemos cantidades diferentes tú, tu hermano y yo, entonces creo que aún nos falta algo, ¿No?
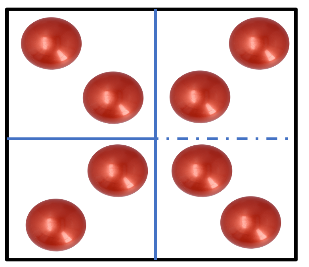
Así es, aunque parece que dividiste entre 3, también tienes que pensar que, para que puedas ver qué fracción corresponde a la parte que te tocó a ti y qué parte le tocó a tu hermano, es necesario analizar qué parte del total de pelotas de tenis representan esas dos que cada uno tiene, por lo que quedaría nuestro reparto como se observa en la imagen.
Entonces es como si lo repartiéramos entre 4 personas, por lo que me tocó al final de las pelotas de tenis al igual que a tu hermano y a ti le tocaron dos cuartos del total, entonces si la mitad de es ¿La mitad de es ? Así es, ahora me gustaría invitarte a resolver un ejercicio de nuestro libro de desafíos.
Resuelve un ejercicio del libro, niñas y niños, y así seguimos reflexionando sobre esto de las fracciones. Para este ejercicio es necesario su libro de desafíos en la página 81.
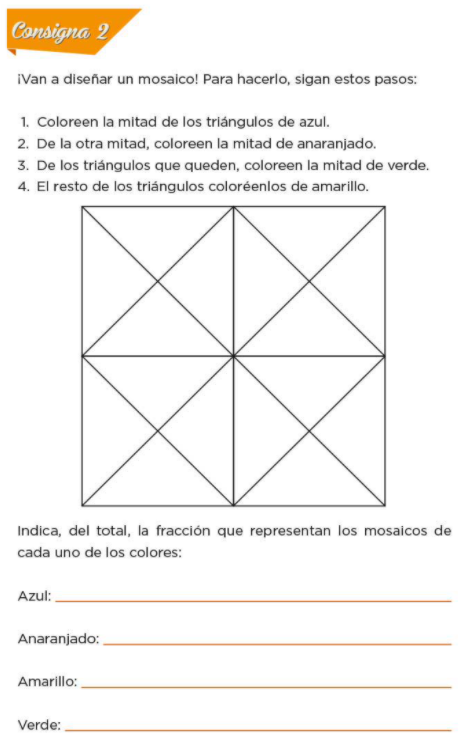
Ve la consigna 2. Vas a diseñar un mosaico, para hacerlo, sigue estos pasos:
- Coloreen la mitad de los triángulos de azul.
- De la otra mitad, coloreen la mitad de anaranjado.
- De los triángulos que queden, coloreen la mitad de verde.
- El resto de los triángulos coloréenlos de amarillo.
Entonces para comenzar vayamos con el primer paso que dice “Coloreen la mitad de los triángulos de azul”. ¿Qué hay que hacer para saber cuál es la mitad de los triángulos?
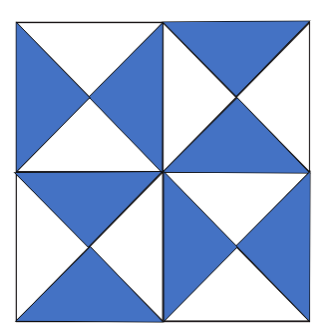
Si tenemos 16 triángulos, por lo que la mitad de ellos son 8, colorea entonces 8 triángulos, ¡ilumínalos! en tu libro de texto vamos 1, 2, 3, 4, 5, 6, 7 y 8.
De la otra mitad, coloreen la mitad de anaranjado, quedaron 8 entonces la mitad de 8 son 4 triángulos.

De los triángulos que queden, coloreen la mitad de verde. Quedaron 4 entonces la mitad de 4 son 2.

Vamos con la última instrucción “El resto de los triángulos coloréalo de amarillo.” bien, quedaron 2 y nos mencionan que ilumina el resto por lo cual ilumina los 2 faltantes.
Recuerda que era la mitad, y eso se representa así: eran 8 triángulos iluminados del total de 16 triángulos,
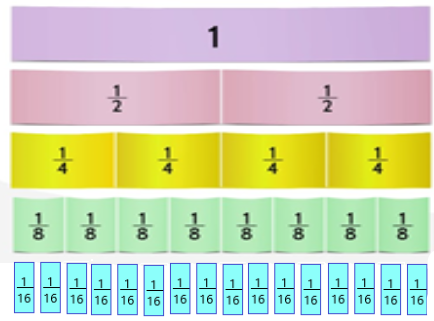
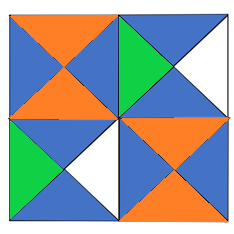
Así es, así como lo viste con el ejemplo del reparto de la sandía cuando dividimos la sandía en 8 pedazos y puedes observarlo más claro con nuestro fraccionario: Rn el fraccionario puedes observar que y son equivalentes ya que representan una misma cantidad.
Entonces en la segunda pregunta que dice: “total de fracción que representa el color naranja” sería 4 de los 8 triángulos, es decir sí, y su fracción equivalente es la mitad de es
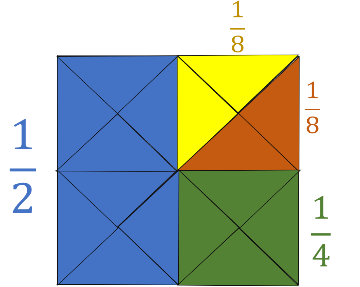
Entonces es fácil, el color amarillo y verde serían cada uno, porque representan también a 2 de los 16 triángulos, es decir, cada color es igual a vamos a verlo en esta otra imagen donde juntamos los triángulos de cada color para que se aprecien mejor las fracciones del entero que representan.
“Una fracción es la forma de expresar una cantidad dividida en partes iguales”.
Y como has visto justo las fracciones te ayudan a repartir o dividir enteros u objetos como la cartulina que repartiste en una clase e inclusive el tiempo, sí y las fracciones te ayudaron hoy a diseñar un mosaico.
Éstas se componen de dos cifras.
El numerador corresponde al número que nos indica cuántas partes tomamos y la siguiente dice, el denominador nos indica en cuántas partes se divide la unidad, el objeto o el entero. Así es, el denominador nos dice en cuántas partes repartimos o dividimos el entero y el numerador nos indica cuántas de esas partes son las que tomamos.
Y la última dice “las fracciones son muy usadas, aunque no lo veamos; las usamos al repartir objetos o al pedir cierta cantidad de un producto, como tortillas, o para medir el tiempo como nuestra clase que dura de hora”.
Recuerda todo lo que has trabajado en la sesión con el uso de las fracciones, pues recorriste el camino fraccionando distancias, repartiste pelotas de tenis.
Por eso es importante recordarlas y continuar trabajando y jugando con ellas.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lectura
