Desarrollo plano de cilindros y conos
Desarrollo plano de cilindros y conos
Aprendizaje esperado: resuelve problemas que implican calcular el volumen de cilindros y conos o cualquiera de las variables que intervienen en las fórmulas que se utilicen. Anticipa cómo cambia el volumen al aumentar o disminuir alguna de las dimensiones.
Énfasis: elaborar los desarrollos planos del cilindro y del cono.
¿Qué vamos a aprender?
Los materiales que utilizarás es tu cuaderno de apuntes, bolígrafo, lápiz y goma.
¿Conoces las figuras sólidas?
Seguramente conoces el cubo, prisma, pirámide, cilindros y esfera.
¿Qué hacemos?
Las figuras geométricas sólidas —también conocidas como formas o cuerpos geométricos— tienen tres dimensiones: longitud, profundidad y altura. Esto quiere decir que son figuras que tienen volumen. Por ello, puedes decir que ocupan un lugar en el espacio.
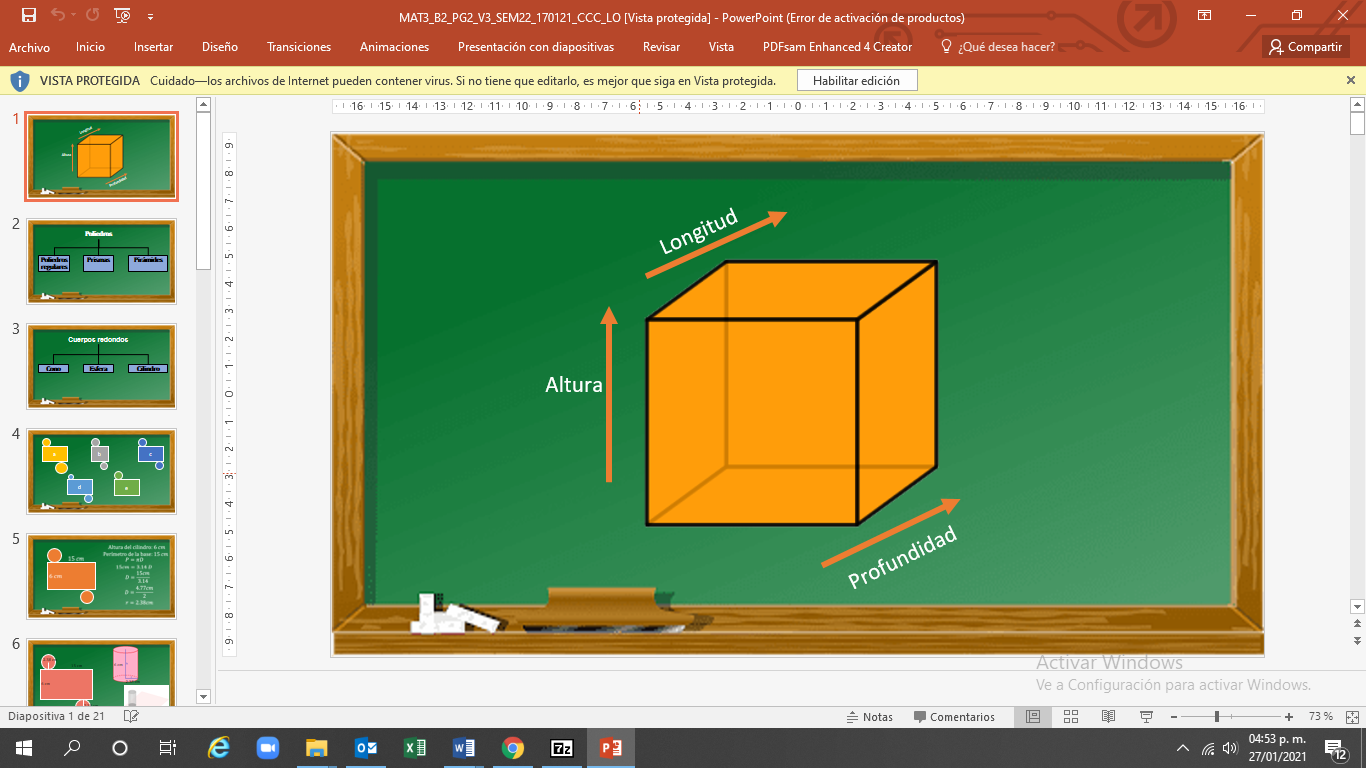
Existen dos tipos de figuras geométricas sólidas y son: los poliedros y los cuerpos redondos. La palabra poliedro proviene del griego “poly” que significa “pluralidad o varios” y “edra”, que significa base o caras.
Son formas geométricas que poseen varias caras y que además son planas. Entre ellas están poliedros regulares, prismas y pirámides
En el cotidiano, puedes encontrar objetos que tienen formas de poliedros. ¿Cuáles ejemplos te has encontrado?
Puede ser un cubito de hielo, una pirámide y un envase de leche.
Entonces en tu hogar tienes diversos tipos de figuras geométricas sólidas y también encuentras los cuerpos redondos.
Los cuerpos redondos son aquellas figuras compuestas por superficies curvas en su totalidad, o que muestran superficies planas y curvas. Entre los cuerpos redondos más comunes encuentras el cono, la esfera y el cilindro.
Los cuerpos redondos los encuentras en la forma de una bola de billar o en un bote de pintura.
Seguramente puedes darte cuenta de que, prestando un poco de atención en los detalles, estás descubriendo estas formas en el cotidiano.
En esta sesión estudiarás dos de estas figuras geométricas sólidas —el cilindro y el cono—. De este modo, se conocerá el desarrollo plano de estas figuras. ¿sabes qué es un desarrollo plano?
En la escuela trabajabas sobre una hoja y hacías un esquema para conocer cómo sería si desplegaras una figura geométrica sólida. Y al componerla, formabas la figura en tres dimensiones.
De los siguientes desarrollos planos, ¿cuál consideras que pueda formar un cilindro?
Observando con cuidado, se tiene que en la figura “a” los dos círculos son de diferente tamaño. En la figura “b”, el rectángulo es corto y no completa el perímetro de los círculos. En la figura “c”, se ve proporcionalidad entre el perímetro de los círculos y el rectángulo. Y en la figura “d” uno de los círculos es menor en su perímetro con respecto al otro, mientras que a la figura “e” le falta un círculo.
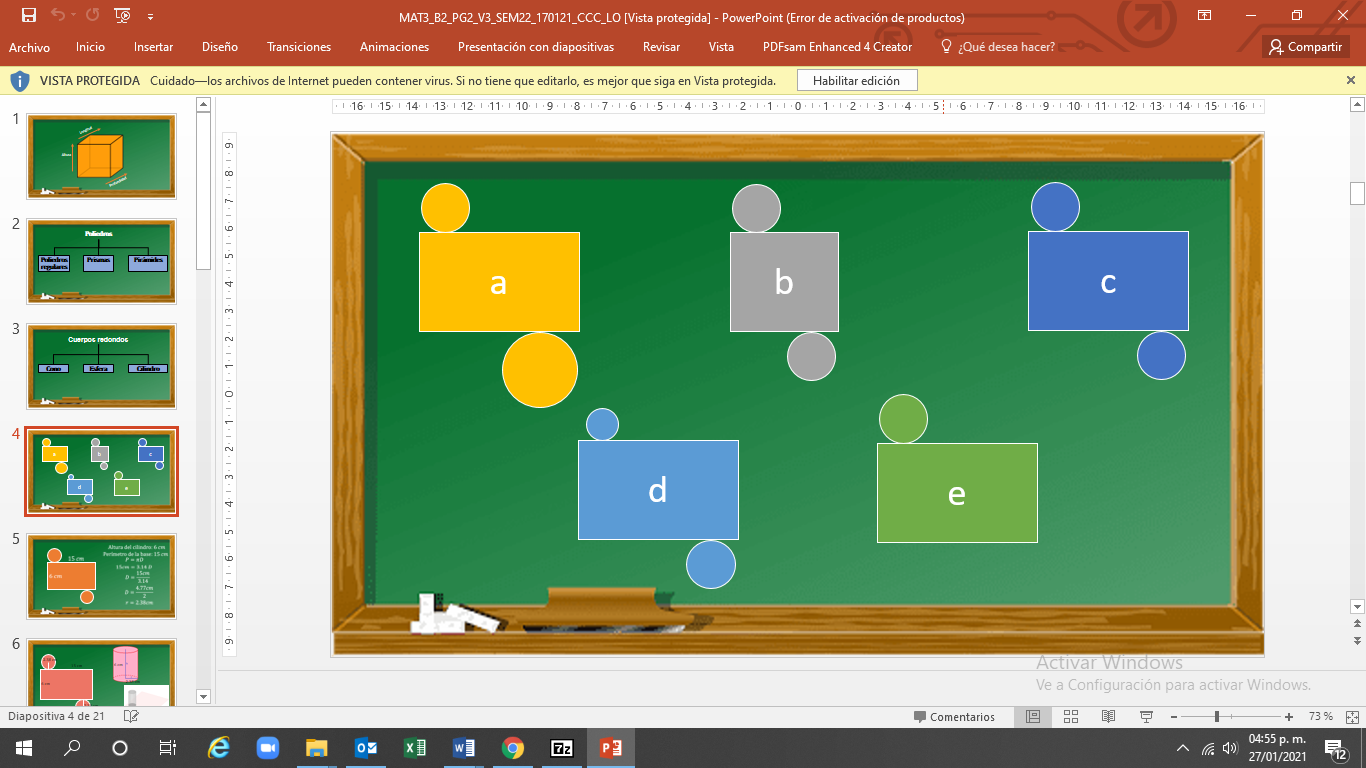
En este caso el desarrollo plano que permite construir el cilindro es el “c”.
Una de las características que debe de tener un desarrollo plano para que, a partir de éste, se pueda elaborar un cilindro es que el rectángulo debe tener de largo la misma distancia que tiene el perímetro de la circunferencia.
Ahora trazarás un desarrollo plano para elaborar un cilindro que tiene de altura 6 cm y un perímetro en la base de 15 cm. ¿Cómo construyes este desarrollo plano?
Considerando que el perímetro de la base es 15 cm, lo primero que harás será encontrar el diámetro de la circunferencia para poder determinar el radio y después construir el círculo del desarrollo plano.
Entonces, realiza los cálculos matemáticos para encontrar el radio de la circunferencia y elaborar el desarrollo plano.
Calcula el diámetro, y para ello utiliza la fórmula “perímetro es igual a pi por diámetro”.
No olvides que el valor de “pi” es una constante, y considerarás que tiene un valor de 3.14.
Sustituye los valores en la fórmula y tienes 15 cm igual a 3.14 por diámetro.
Despeja el diámetro y es igual a 15 cm entre 3.14.
Divides y obtienes como resultado 4.77, y para obtener el radio lo divides entre 2.
El radio es igual a 2.38 cm.
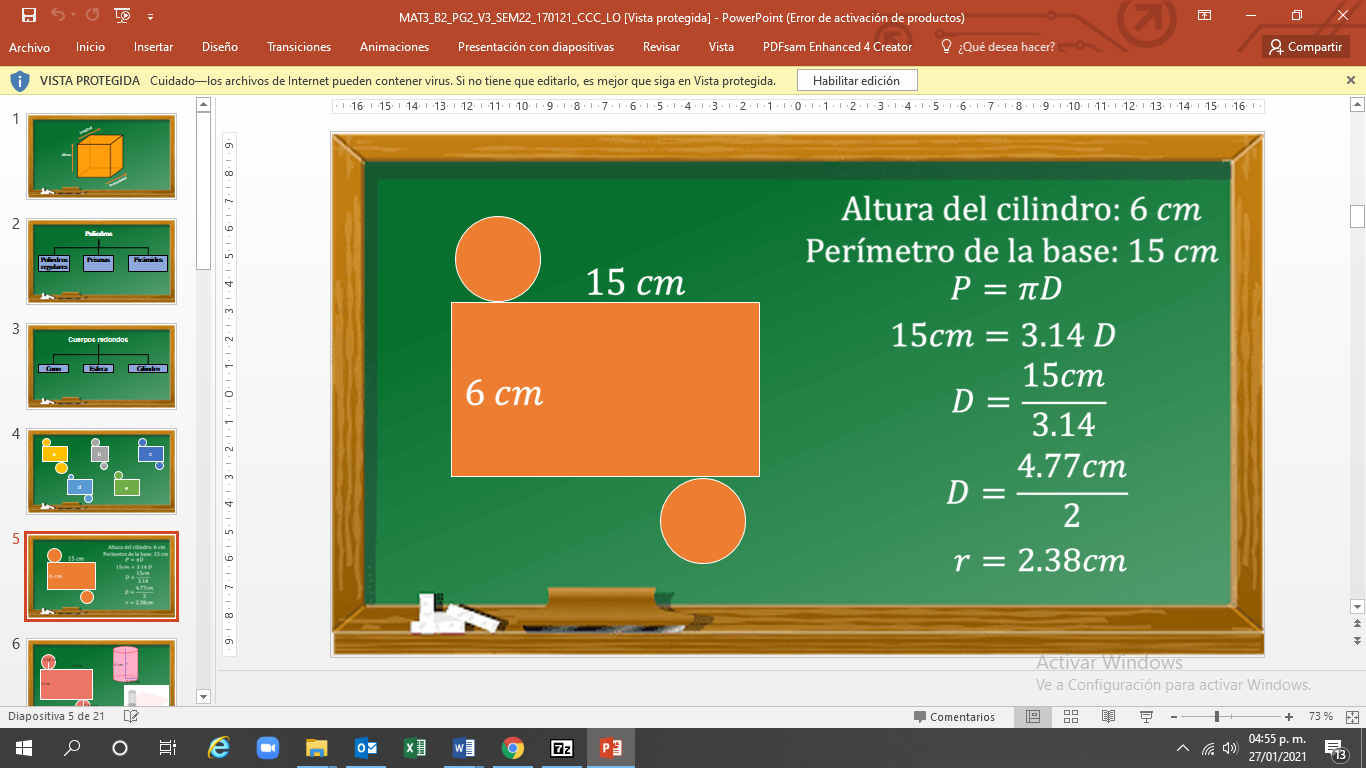
Con esta información construye los círculos para el desarrollo plano y, finalmente, arma el cilindro que tiene una altura de 6 cm y un radio de 2.38 cm.
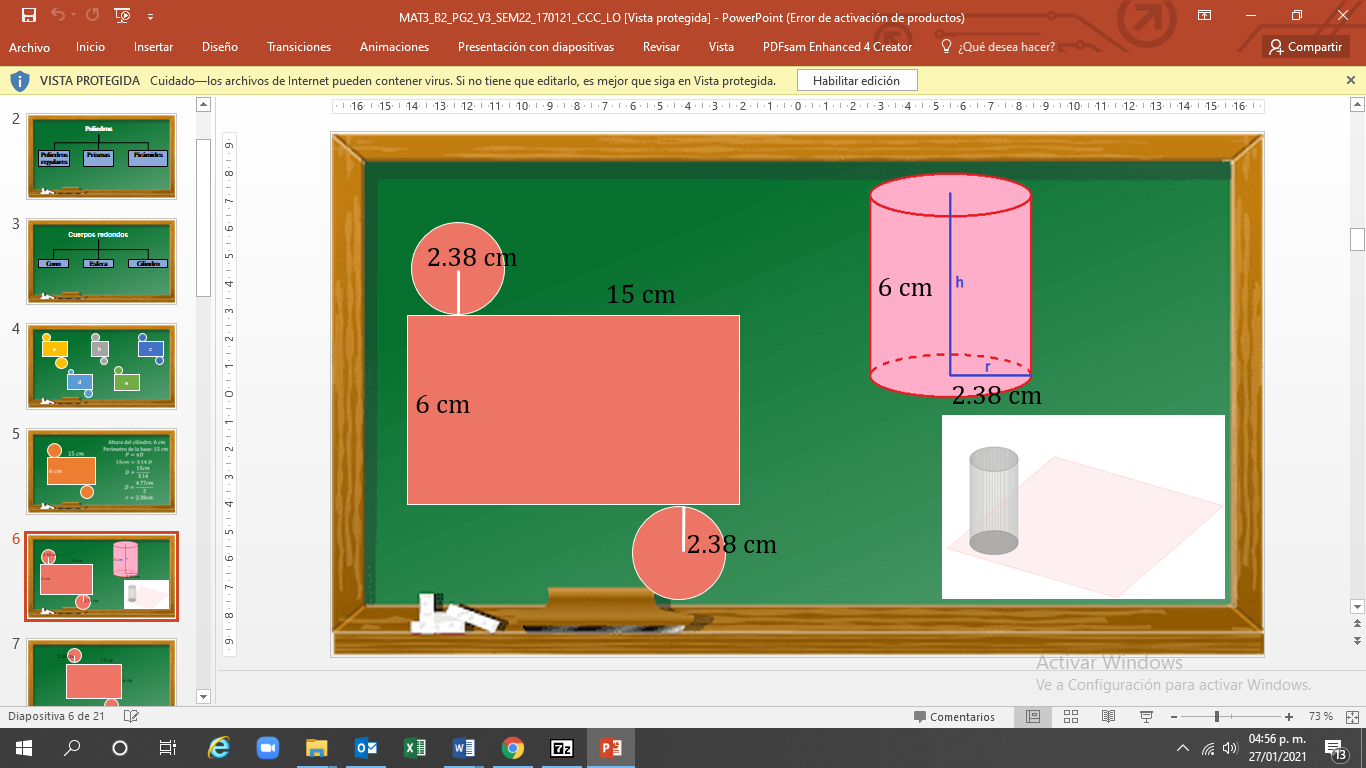
Recapitulando, ¿cuánto mide la cara curva del cilindro? Es decir, el largo y ancho del rectángulo.
El rectángulo mide de largo 15 cm y de ancho 6 cm.
¿Cuánto mide el radio de la circunferencia trazada?
El radio es de 2.38 cm.
¿Y cómo calculas la medida del radio?
Emplea la fórmula del perímetro del círculo. Primero sustituye los valores en la fórmula. Posteriormente, despeja la incógnita, que en este caso es el diámetro. Una vez obtenido este dato, lo divides entre 2, debido a que el radio es la mitad del diámetro.
Las medidas del cilindro tienen como resultado: 2.38 cm de radio, 6 cm de altura y 15 cm de largo.
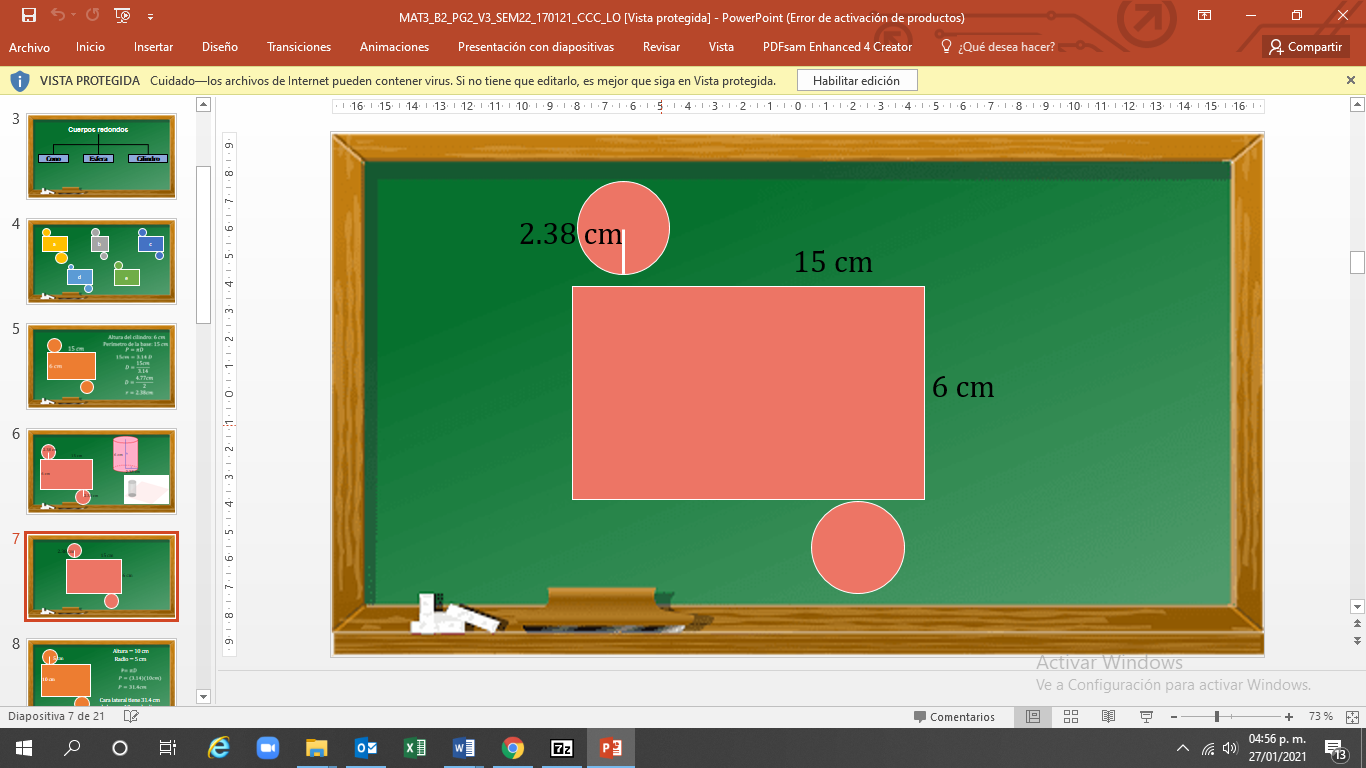
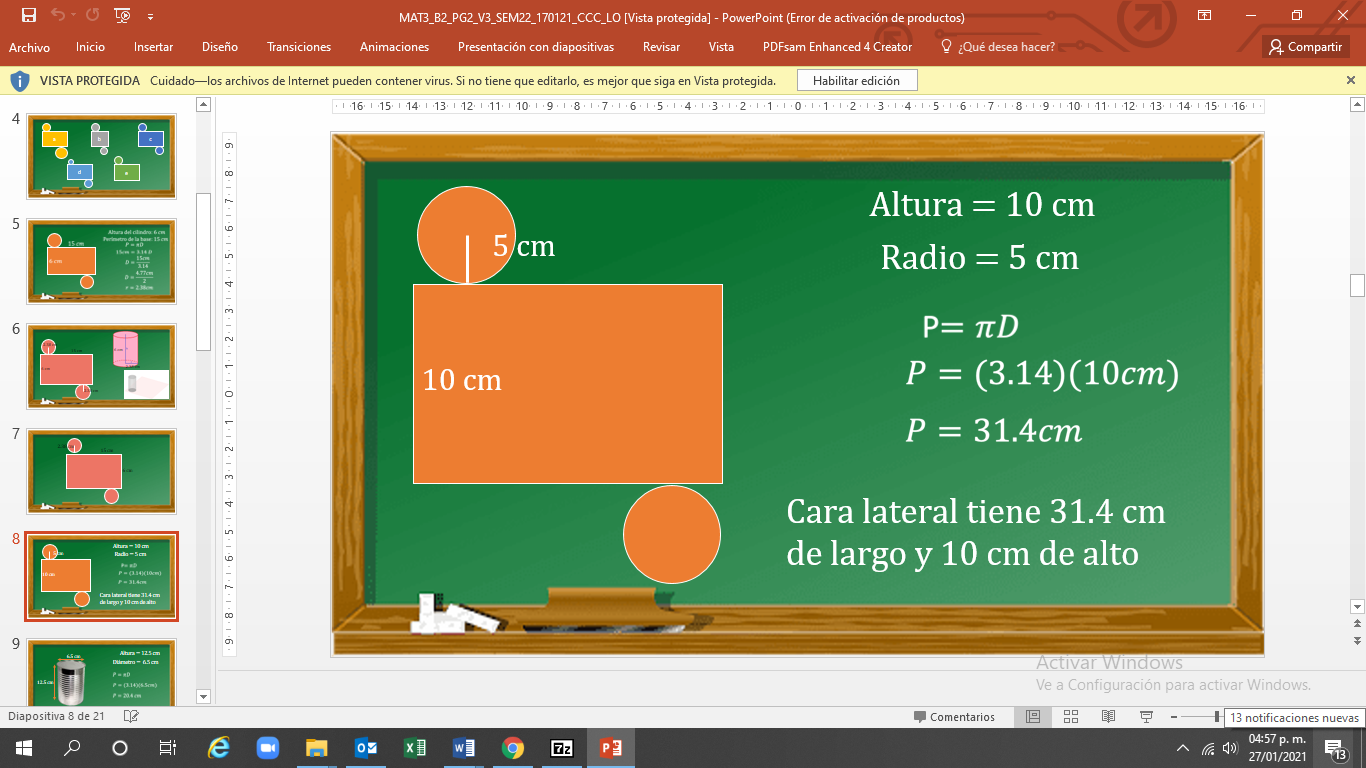
Si analizas, la cara lateral de un cilindro es un rectángulo cuyas medidas corresponden a la altura del cuerpo y el perímetro de su base. Pero, ¿qué medidas tiene la cara lateral de un cilindro de 10 cm de altura y 5 cm de radio?
Para calcularlo, lo primero es utilizar la fórmula del perímetro del círculo —que es igual a pi por diámetro—, donde pi equivale a 3.14.
Sustituyes los valores, y el perímetro es igual a 3.14 por 10, ya que el radio al ser 5, el diámetro es el doble.
Realiza la operación y el perímetro es igual a 31.4 cm.
Así el largo de la cara lateral de este cilindro es igual a 31.4 cm y su altura 10 cm.
Analiza el siguiente problema.
Una lata con forma cilíndrica tiene las siguientes medidas: alto 12.5 cm y diámetro 6.5 cm. Calcula las dimensiones de su cara lateral.
Lo que tienes que hacer es utilizar la fórmula del perímetro del círculo, que es igual a pi por diámetro.
Sustituye los valores en la fórmula, y el perímetro es igual a 3.14 por 6.5 cm.
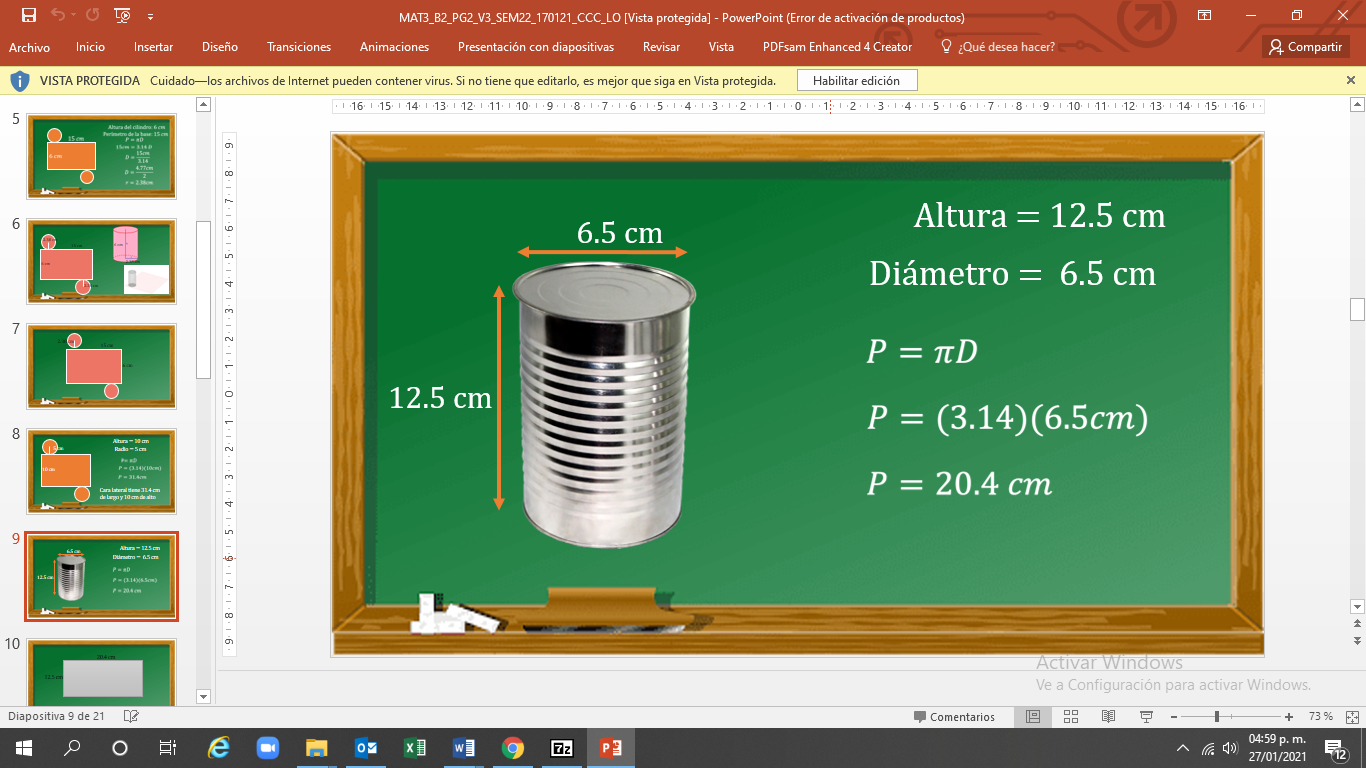
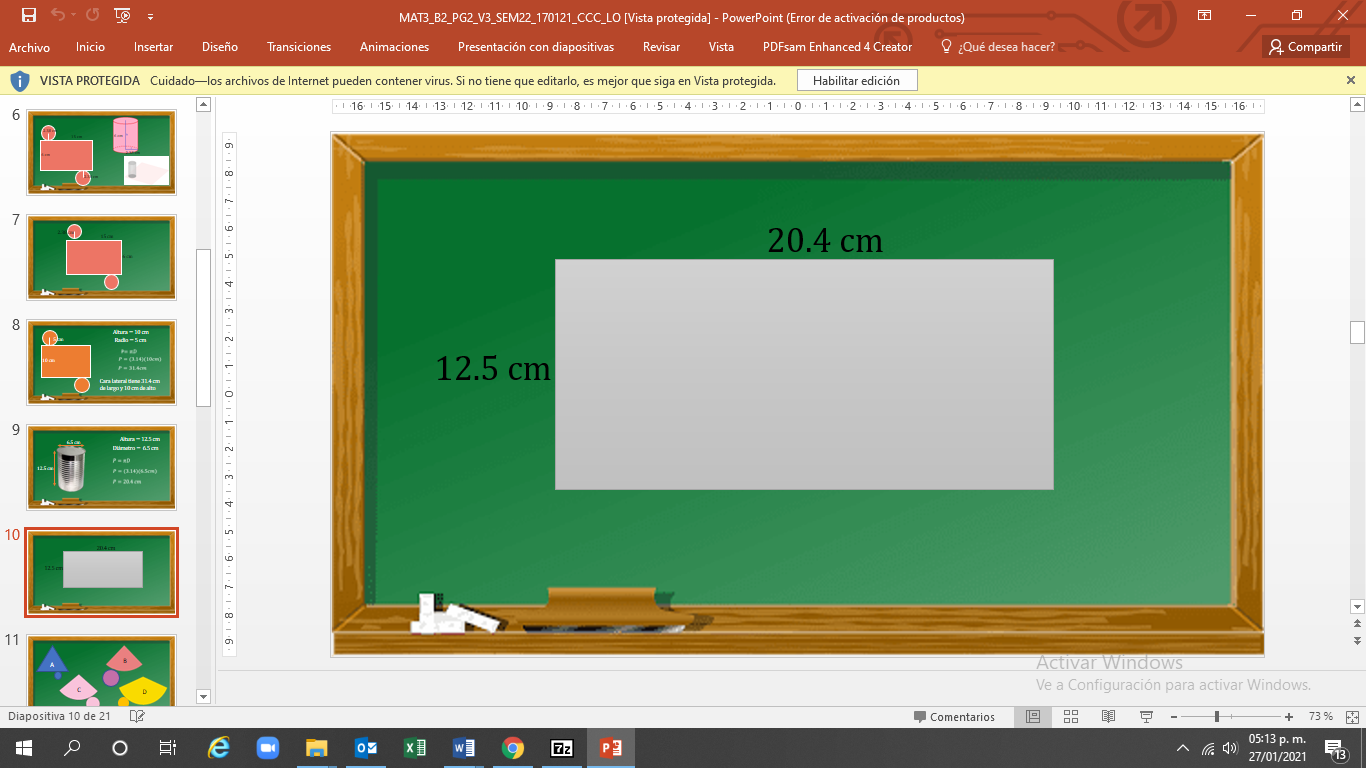
Al realizar las operaciones se tiene que el perímetro es igual a 20.4 cm. Así, el largo del rectángulo que forma la cara lateral es igual a 20.4 cm y el ancho es igual a 12.5 cm.
¿Te has preguntado cómo se construye un cono?
De las siguientes imágenes, ¿cuál opción corresponde con el desarrollo plano de un cono?
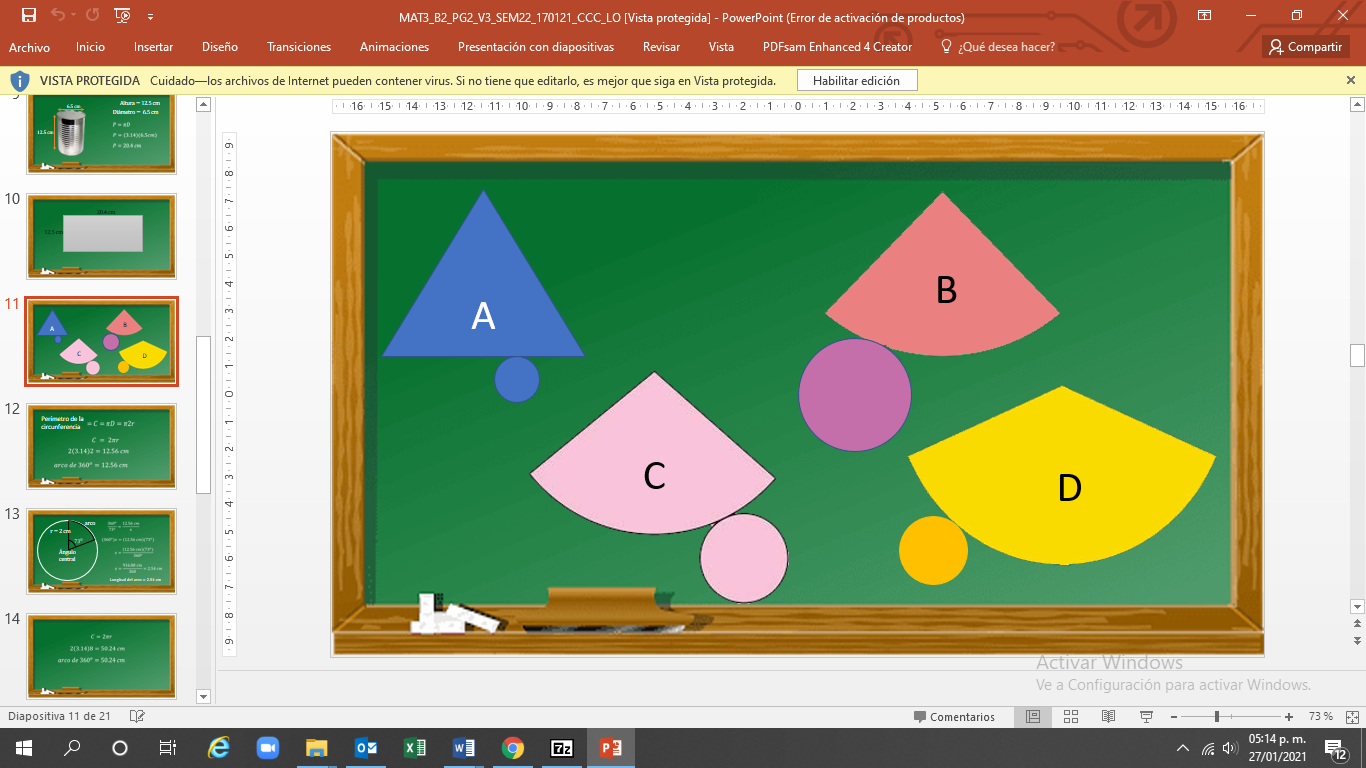
Es la “c”.
Ahora, 3 de las figuras anteriores constan de un arco con un sector circular y un círculo —elementos necesarios para elaborar un cono—. Sin embargo, sólo en una el arco del sector circular tiene la misma longitud que la circunferencia del círculo.
Analiza lo siguiente, para conocer el desarrollo plano del cono.
Para calcular la longitud de un arco se debe tener en cuenta lo siguiente:
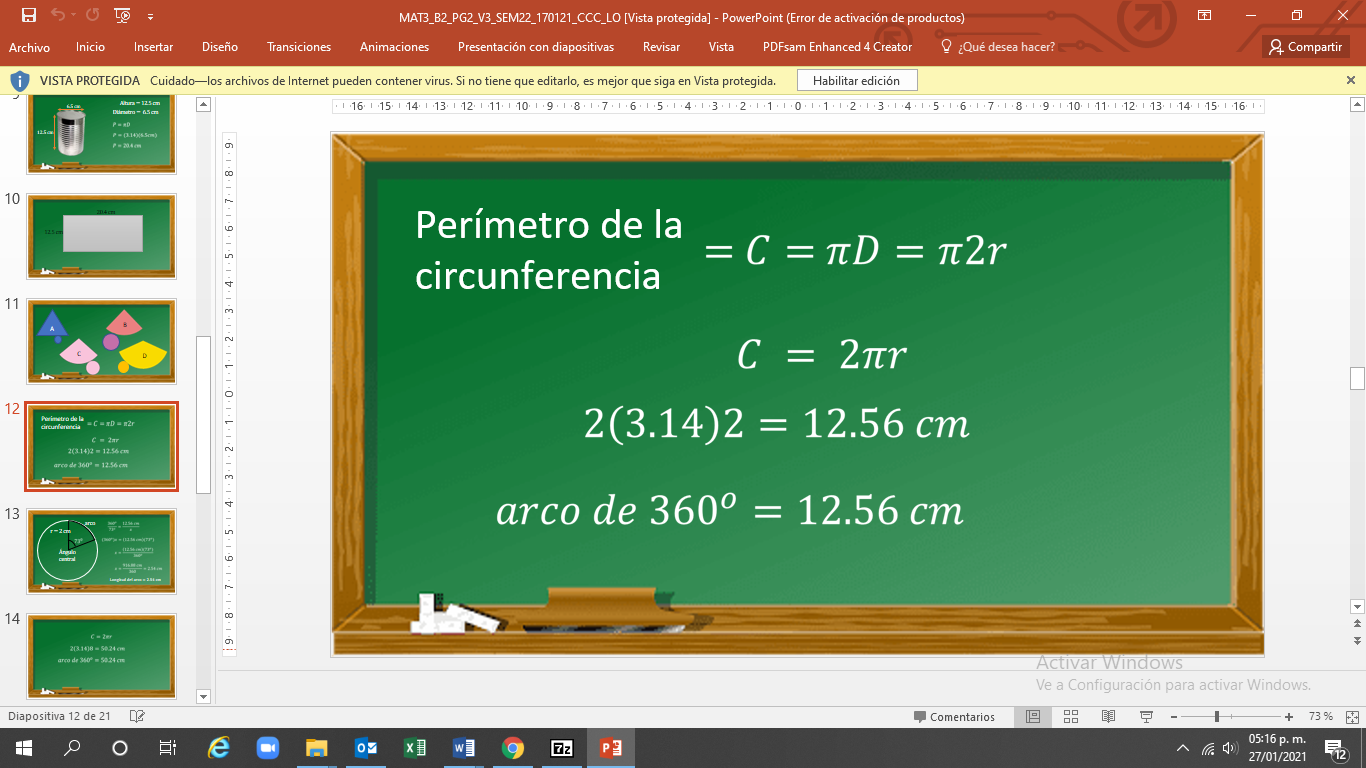
Si una circunferencia de 2 cm de radio estuviera completa mediría 2 pi por radio —que es aproximadamente 2 por 3.14 por 2—, que es igual a 12.56 cm.
Esto corresponde a los 360° de la circunferencia completa. Esto quiere decir que 360° corresponde al perímetro total de la circunferencia, que en el ejemplo es igual a 12.56 cm.
Observa cuando el arco abarca un ángulo de 73°, por lo que se plantea el siguiente problema:
Si en una circunferencia con 2 cm de radio, a un ángulo de 360° le corresponde una circunferencia de 12.56 cm. ¿Qué longitud le corresponde a un ángulo de 73°?
Sabes que 360° es igual a 12.56 cm, y 73° es igual a “x”. Por lo tanto, tienes una ecuación de primer grado.
Si despejas “x”, se tiene que 360° por “x” es igual a 12.56 cm por 73°.
“x” es igual a 12.56 cm por 73°, todo esto entre 360°
Se eliminan los grados y “x” es igual a 916.88 cm entre 360…
De este modo, “x” es igual a 2.54 cm.
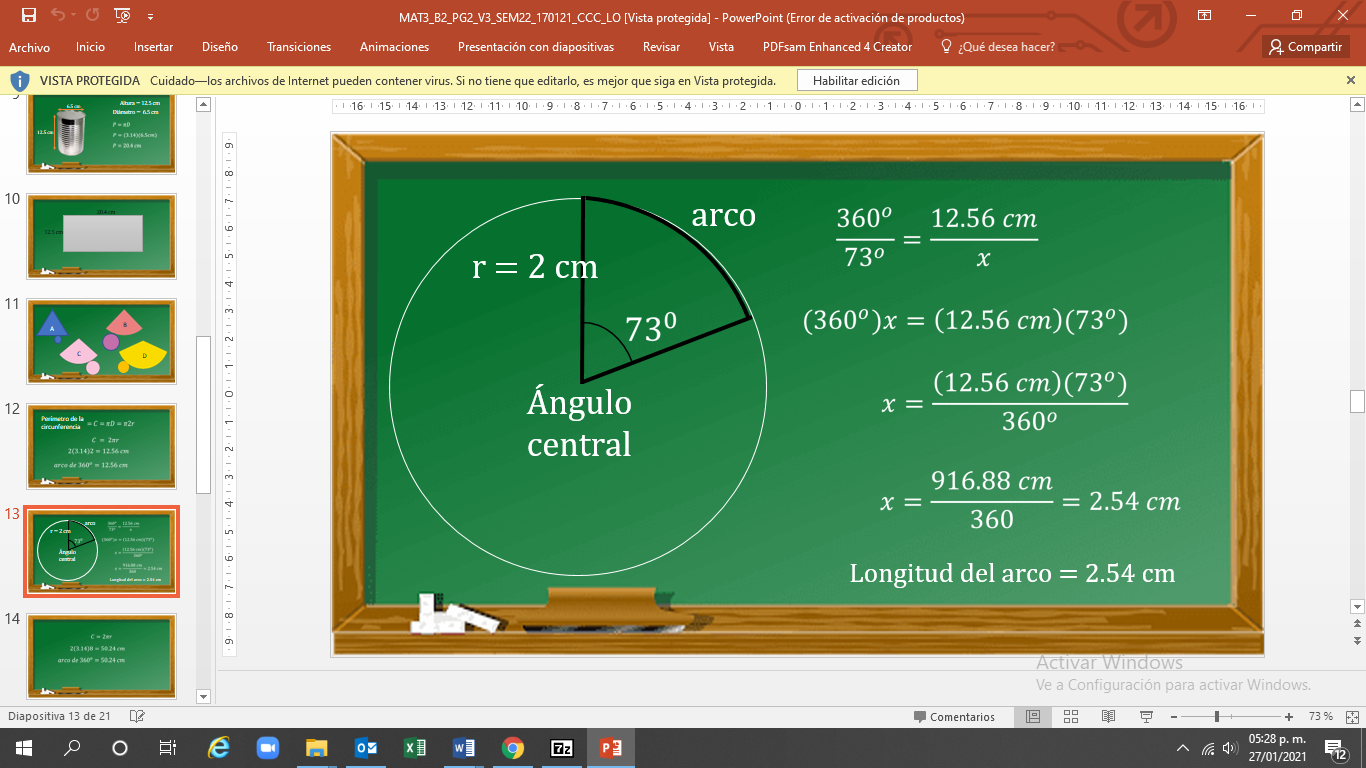
Entonces, la longitud del arco es igual a 2.54 cm.
Una vez identificadas estas dos relaciones, ¿puedes trazar el desarrollo plano de un cono?
Sí, una vez identificada esta relación puedes elaborar el desarrollo plano de cualquier cono.
Con los siguientes datos: radio del sector circular, 8 cm, y ángulo central, 120°, con ellos puedes elaborar el desarrollo plano para un cono.
Realiza los cálculos siguientes para elaborar el desarrollo plano del cono que propones.
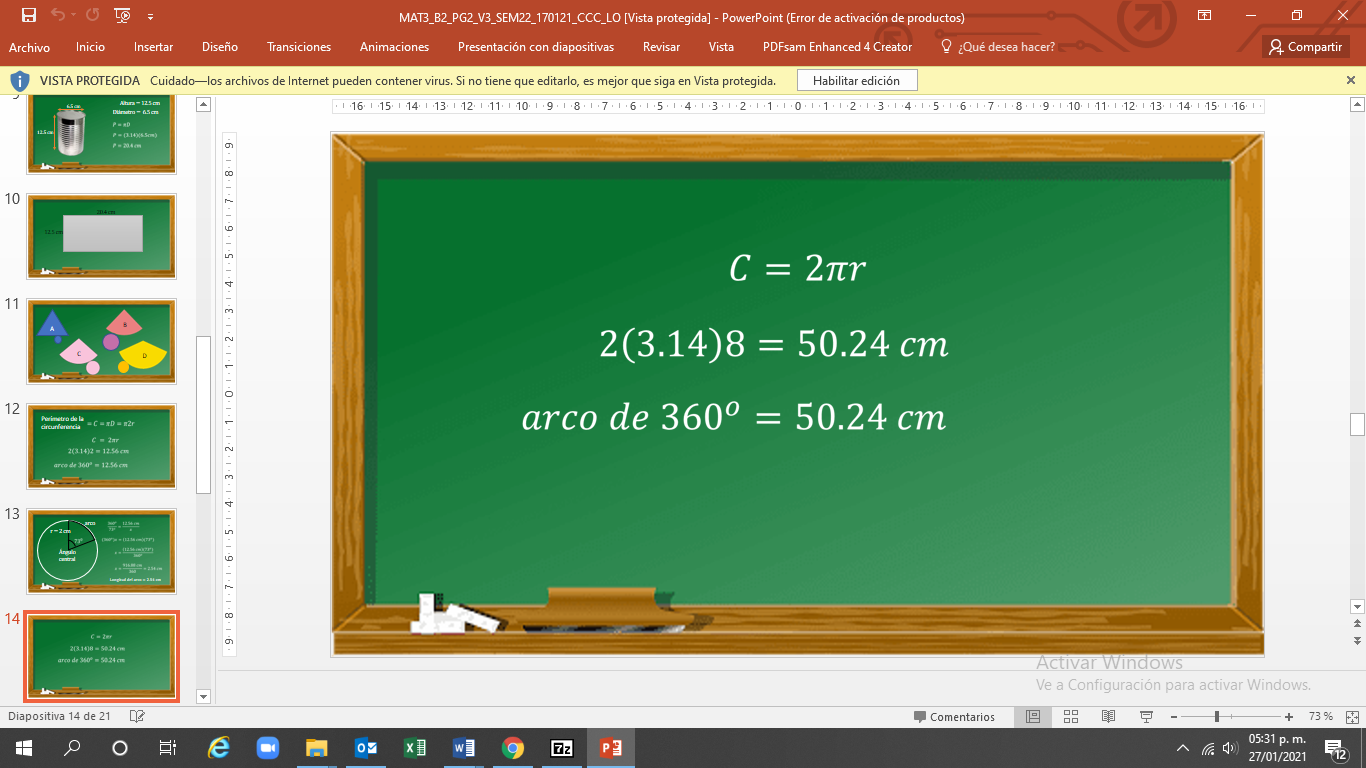
Haciendo uso de la fórmula de la circunferencia, encuentra la relación de los grados de la circunferencia:
Sustituyes los valores, tienes 2 por 3.14 por 8 es igual a 50.24 cm. Es así como estableces que el arco de 360° es igual a 50.24 cm.
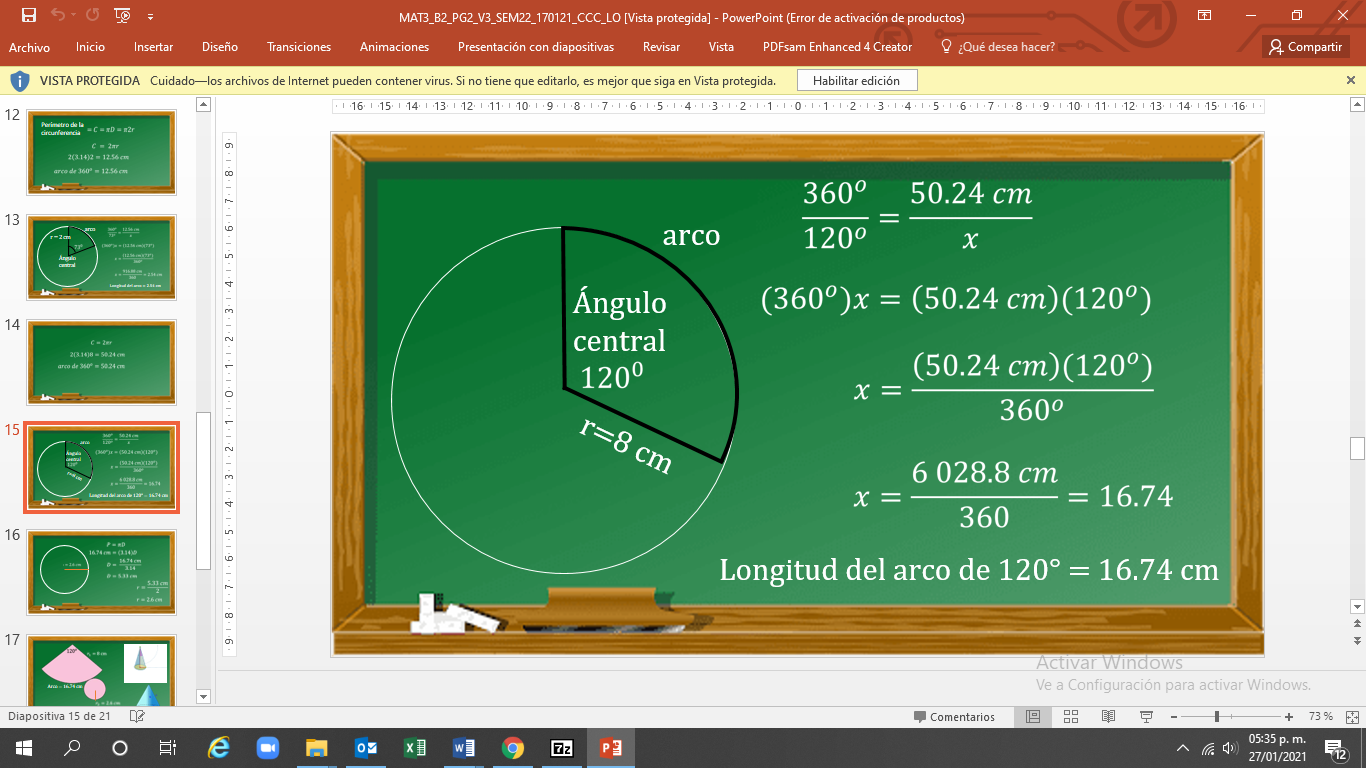
En la relación 360° es a 50.24 cm como 120° es a “x”.
Se tiene con esto una ecuación de primer grado. Por lo tanto, se despejan los términos 120 y “x”.
Así se obtiene que 360 por “x” es igual a 50.24 cm por 120°.
Y al despejar, se obtiene que “x” es igual a 50.24 cm por 120°, todo esto entre 360°.
“x” es igual a 6 028.8 cm entre 360.
“x” es igual a 16.74 cm.
La longitud del arco de 120° es igual a 16.74 cm.
Una vez que tienes todos estos datos, ¿puedes construir el cono?
Sólo te hace falta conocer el radio de la base.
Para obtener ese dato debes hacer lo siguiente:
Partes de la fórmula del perímetro de la circunferencia:
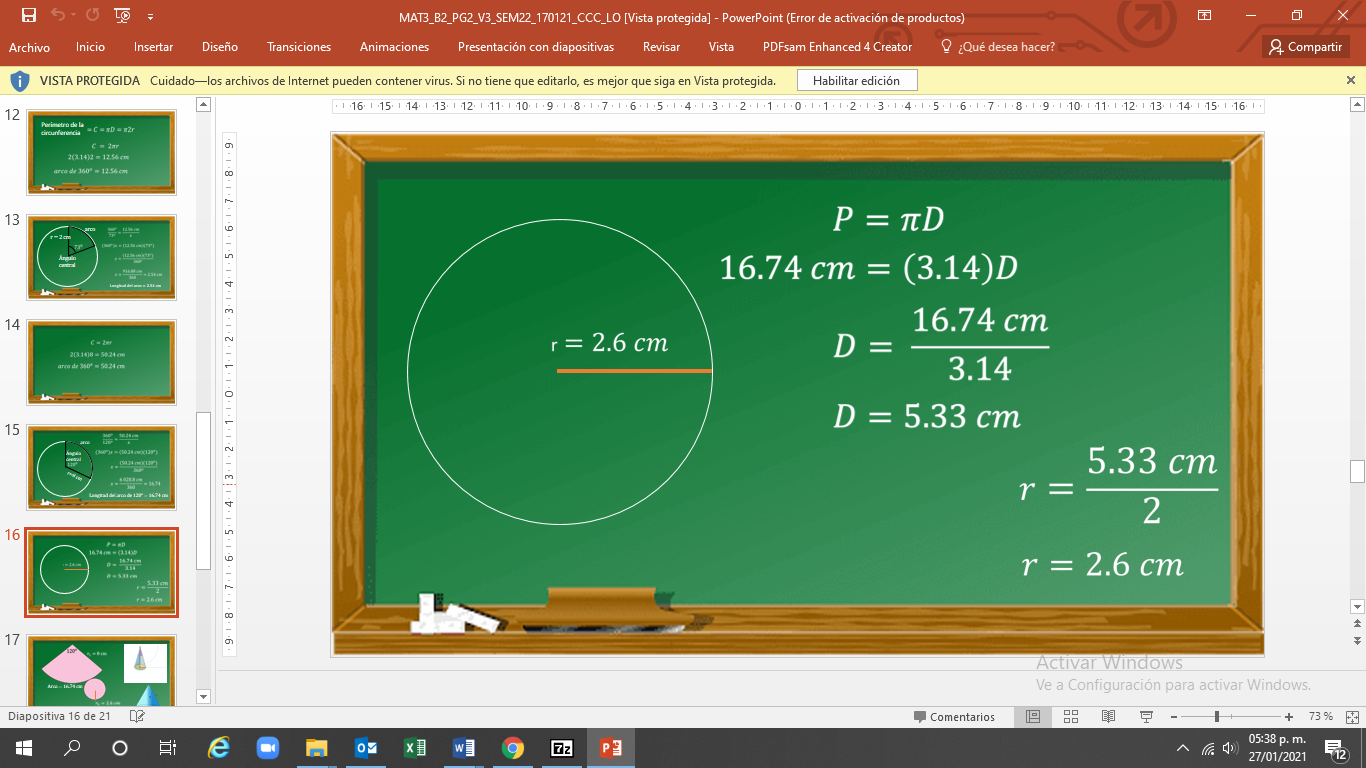
Sustituyes los valores y tienes que 16.74 cm es igual a 3.14 por diámetro.
Despejas el diámetro que es igual a 16.74 cm entre 3.14.
Realiza la operación, y tienes que el diámetro es igual a 5.33 cm.
Como requieres conocer el radio de esta circunferencia, lo único que tienes que hacer es dividir entre dos el diámetro.
El radio es igual a 2.6 cm.
Finalmente, trazarás un sector circular que tendrá una apertura de 120° en el ángulo central. El radio (r1) del círculo mayor será igual a 8 cm; la distancia del arco es igual a 16.74 cm y el radio (r2) del círculo menor es igual a 2.6 cm, como se muestra en la figura. Una vez trazada, el desarrollo plano se recorta y se construye el cono.
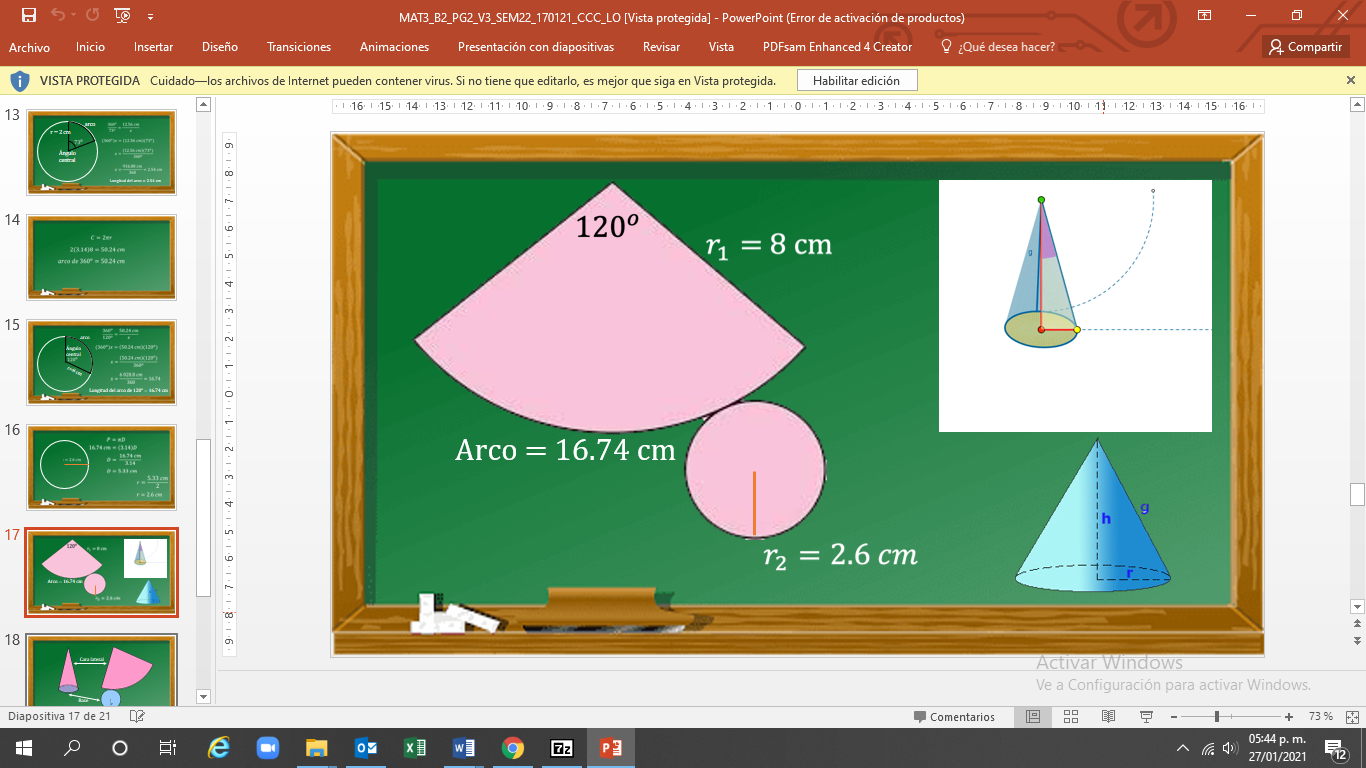
Aunque este método fue útil para construir un cono, existen otros medios para realizarlo.
Es importante establecer la relación entre las medidas de un cono y su desarrollo plano. Considerando que el desarrollo plano del cono está formado por una cara circular llamada base y una cara lateral que es un sector circular.
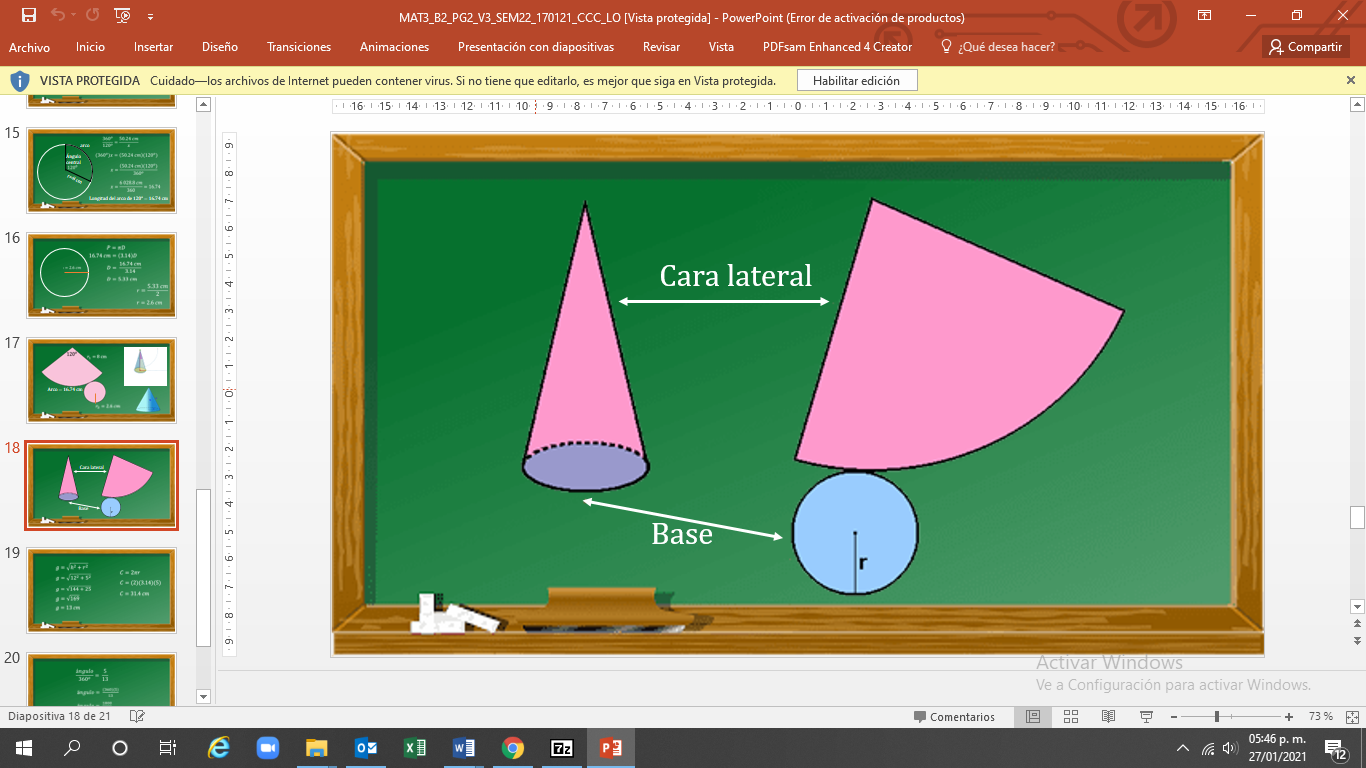
La longitud del perímetro de la circunferencia de la base es igual que la longitud del arco del sector circular. Y aunque la altura del cono varía, la base no cambia. Entonces, la longitud del arco del sector circular tampoco cambia, pero sí cambia el ángulo del sector circular y el radio que lo forma.
Para calcular el área o superficie lateral de un cono necesitas conocer la generatriz, es decir, la distancia entre el vértice y uno de los puntos de la circunferencia de la base. Hay una relación entre la generatriz y la altura del cono. Esta relación está dada por el Teorema de Pitágoras.
Para conocer más, analiza el siguiente problema:
Se quiere construir un cono de 5 cm de radio y 12 cm de altura. Lo primero que se hace es encontrar el valor de la “g”, —es decir, la generatriz—. Para ello te apoyarás en el Teorema de Pitágoras:
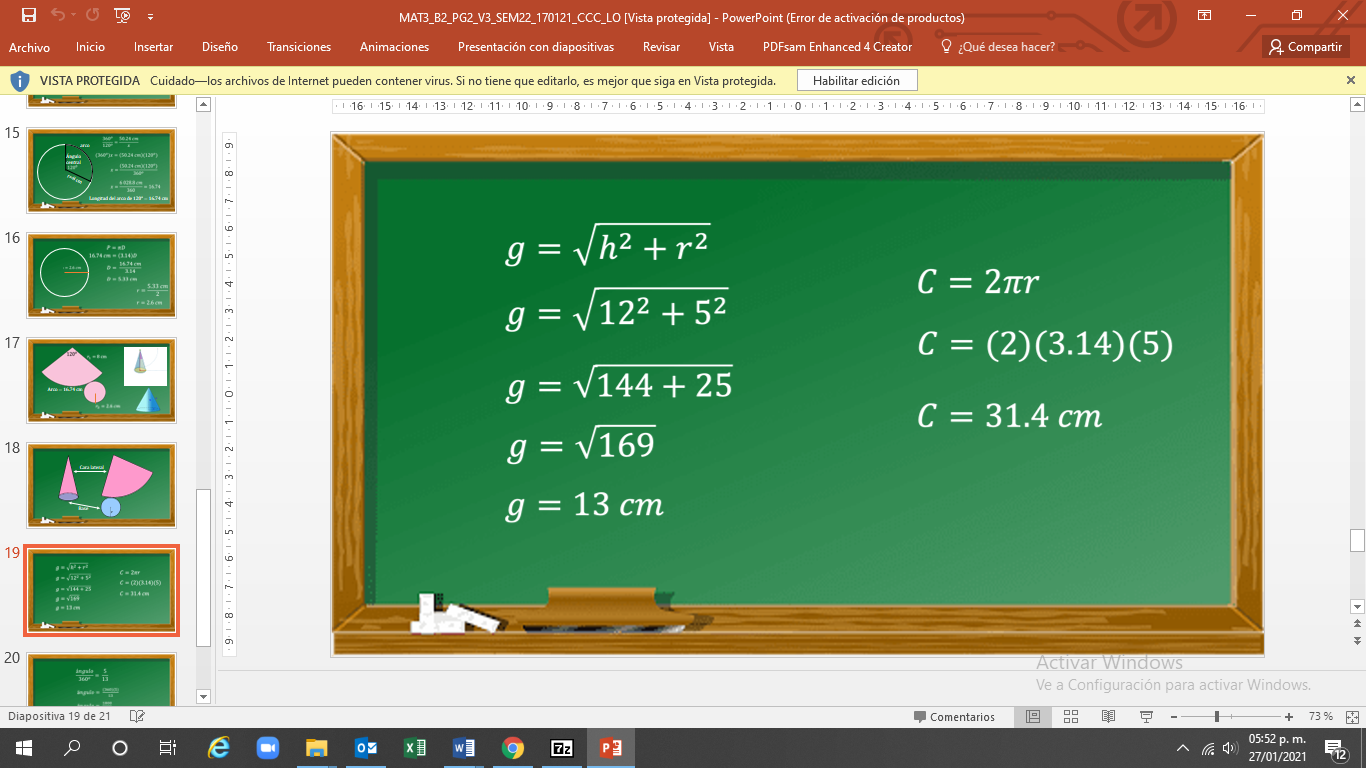
La generatriz es igual a la raíz cuadrada de la altura al cuadrado, más el radio al cuadrado.
Al sustituir los valores, tienes que la generatriz es igual a la raíz cuadrada de la suma de 12 al cuadrado más 5 al cuadrado.
Esto es igual a la raíz cuadrada de 144 más 25.
Así, se tiene que la generatriz es igual a la raíz cuadrada de 169.
Calculando la raíz cuadrada, tienes que la generatriz es igual a 13 cm.
Ahora, calcularás la circunferencia de la base del cono. Ya sabes que la fórmula de la circunferencia es igual a 2 pi por radio.
A sustituir los valores tienes que la circunferencia es igual a 2 por 3.14 por 5.
Al realizar las operaciones se tiene que la circunferencia es igual a 31.4 cm.
Esta será la longitud del arco del sector circular, y el ángulo de dicho sector lo calcularás de la siguiente forma:
El ángulo es a 5 cm como 360° es a 13 cm.
Despejando tienes que el ángulo es igual a 360° por 5 cm entre 13 cm.
Al realizar las operaciones, en el numerador tienes que el ángulo es igual a 1800 entre 13.
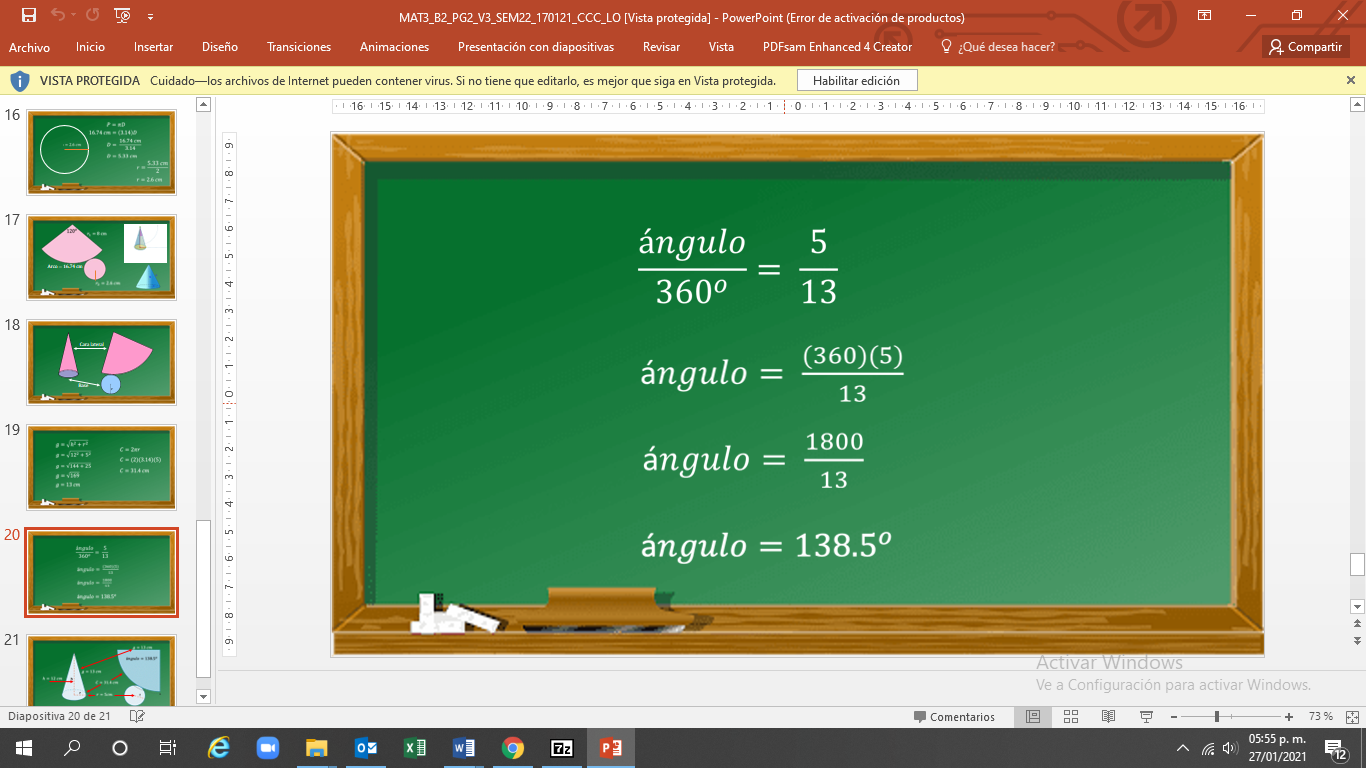
Después de operar, se tiene que el ángulo es igual a 138.5°. Con esta información puedes destacar que: la generatriz es igual a 13 cm; el ángulo central es de 138.5°; el radio del círculo menor es igual a 5 cm; la altura del cono es 12 cm y la longitud del arco es de 31.4 cm.
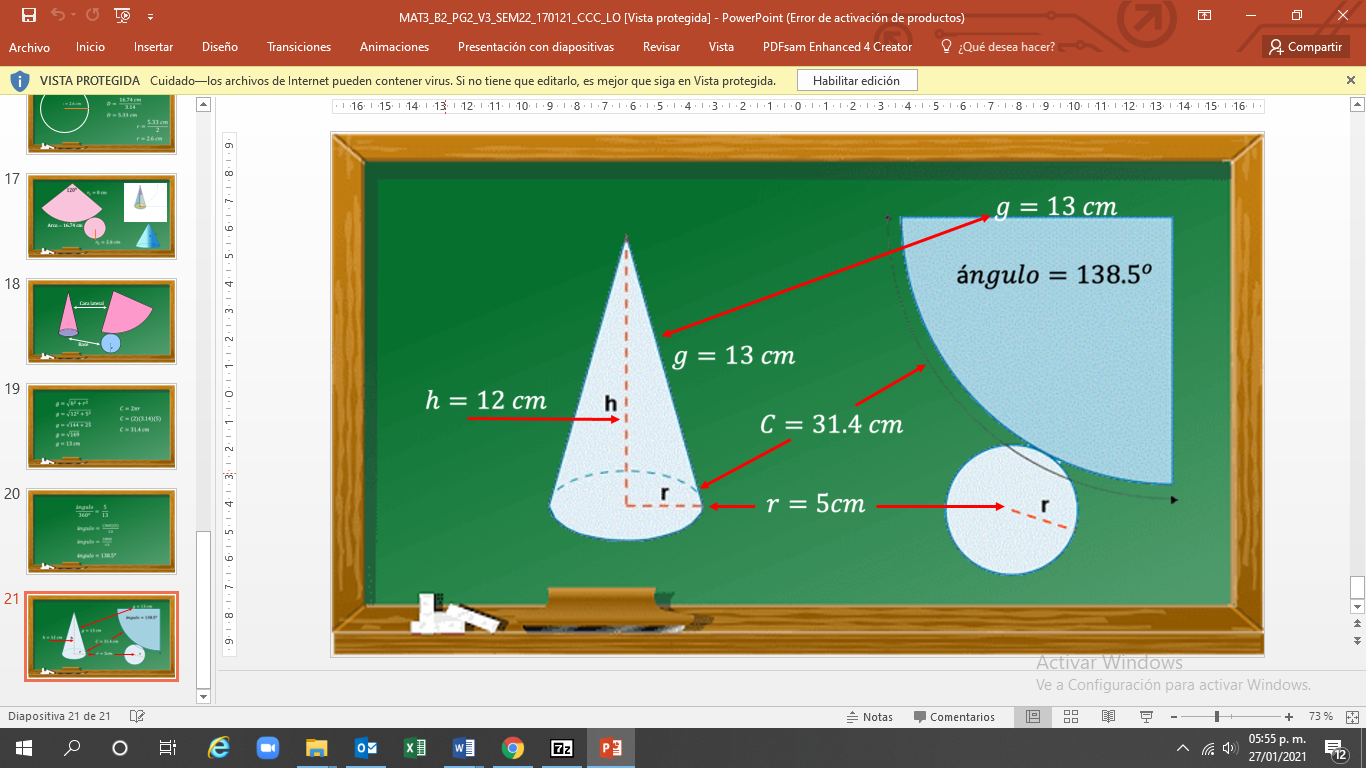
Usando esta información, ya se puede elaborar el desarrollo plano para construir el cono.
Aprendiste que un sólido o cuerpo geométrico es una figura geométrica de tres dimensiones: largo, ancho y alto. Además, estas figuras ocupan un lugar en el espacio y, en consecuencia, tienen un volumen.
Además, están implícitas en la vida cotidiana, es decir las puedes encontrar en el entorno en el que te rodeas.
Sin embargo, entre los cuerpos geométricos existen dos tipos: los poliedros y cuerpos redondos.
Conociste el cilindro y el cono, que son cuerpos redondos:
El cilindro circular es la figura tridimensional que se forma cuando una recta es llamada generatriz. Y éste gira alrededor de otra recta que queda fija, llamada eje.
El cono es un cuerpo de revolución generada al hacer girar un triángulo rectángulo alrededor de uno de sus catetos. Se le llama base al círculo inferior del cono y “g” a las generatrices que se unen en el vértice de este.
El reto de hoy:
Después de esta sesión, puedes resolver algunas situaciones planteadas en tu libro de texto.
Piensa también, en qué otras áreas del conocimiento se puedes emplear lo aprendido.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas