Sucesiones I
Sucesiones I
Aprendizaje esperado: verifica algebraicamente la equivalencia de expresiones de primer grado, formuladas a partir de sucesiones.
Énfasis: explicar la equivalencia de las distintas expresiones algebraicas cuando representan la regla de una misma sucesión.
¿Qué vamos a aprender?
En esta sesión, las actividades están centradas en verificar la equivalencia de expresiones algebraicas a través de la construcción y el análisis de sucesiones numéricas.
Este tema de estudio no es nuevo, pues ya has trabajado con sucesiones de figuras geométricas y numéricas. Además, en tu trayectoria escolar aprendiste a encontrar otros términos de sucesiones mediante la regla que las genera, la describiste con tus propias palabras y, posteriormente, a través de una expresión algebraica. Por lo tanto, reconocerás que existen diversas sucesiones de figuras y que éstas se pueden organizar numéricamente para analizar su comportamiento y así, deducir el número de elementos de acuerdo con el número de posición.
¿Qué hacemos?
En la siguiente imagen se muestran tres arreglos formados por cuadrados. El punto de partida fundamental para comenzar el análisis de una sucesión de figuras es determinar que cada arreglo de la sucesión es un término de esta y esos términos se pueden representar utilizando números. Es decir, el primer arreglo será el término 1 de la sucesión, a continuación, el segundo será el término 2 y así, sucesivamente.
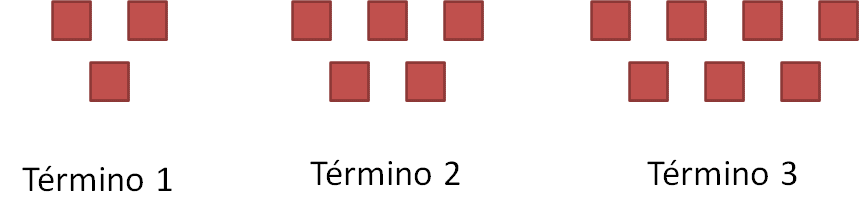
Una vez representada la sucesión de figuras usando números, se pueden hacer observaciones respecto a la manera como se va construyendo el siguiente término. Incluso se pueden dibujar los siguientes términos. Además, los elementos gráficos de la sucesión se pueden analizar numéricamente, convirtiéndolos en una sucesión numérica.
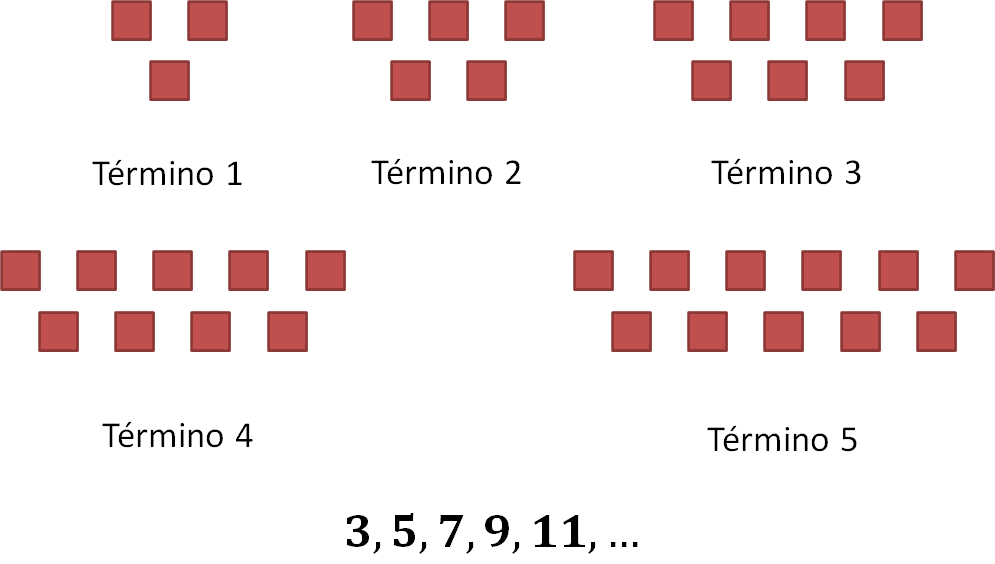
Ahora, escribe con tus propias palabras qué entiendes por sucesión numérica. Después analiza la siguiente definición.
Una sucesión es un conjunto de números ordenados a través de la regla que los origina. Los elementos que forman una sucesión numérica se llaman términos. Los términos que constituyen una sucesión pueden calcularse a través de una regla o patrón que puede describirse por medio de una expresión algebraica o regla general. Los puntos suspensivos, significan que la sucesión continúa, es decir, que no tiene fin.

A continuación, analiza cómo tres alumnos de secundaria explican lo que saben acerca de las sucesiones. Esto, al trabajar con la sucesión de figuras que se usó de ejemplo. Algunos de ellos visualizaron cada término de la sucesión como un conjunto, al cual se agrega cierta cantidad de cuadrados de figura en figura.
Alumno 1:
El alumno 1, identificó que la sucesión de figuras va aumentando de dos en dos, pero eso no fue suficiente para que pudiera definir el comportamiento de la sucesión con una expresión algebraica.
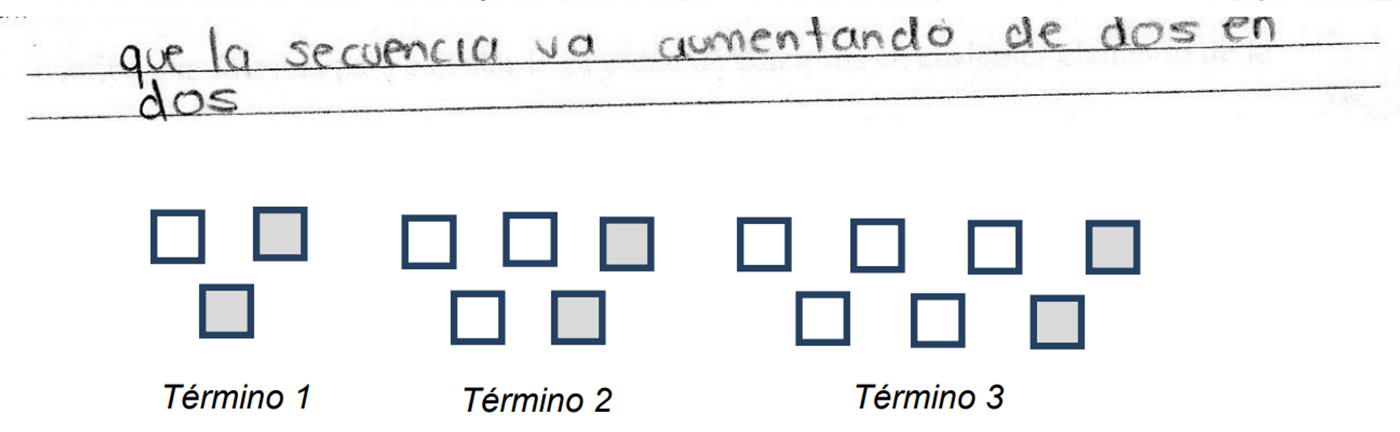
Aunque cabe aclarar que identificar el comportamiento de la sucesión es un primer paso muy importante.
Alumna 2:
La alumna 2, a partir de la visualización, consigue expresar las relaciones entre las figuras y es capaz de explicar y dar razón de los crecimientos y la relación de éstos con la posición que ocupan los elementos de la secuencia.
Ella relaciona la cantidad de los elementos presentes en cada arreglo con el número de término que le corresponde, lo que facilita la construcción de la expresión que genera la sucesión. La expresión general la plantea en función del número de término o de posición, al que habitualmente se le asigna la literal “n”
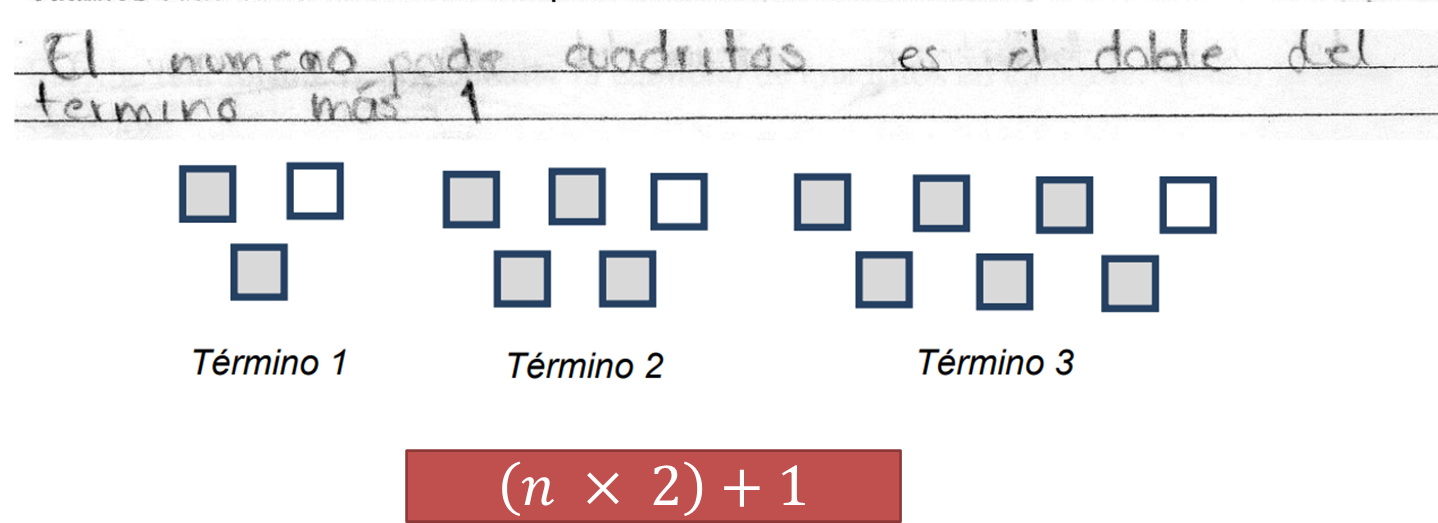
En este caso, la alumna indica que la expresión general de la sucesión es (n x 2) + 1, y es capaz de explicarla: “n” es el término, entonces si el término es uno, se multiplicará por dos, más el uno que siempre va a ser constante.
Después, ella lleva su razonamiento al siguiente caso, es decir, en lugar de “n” coloca 2 y comprueba que obtiene el número de elementos del segundo término, que son 5.
Pero ¿esta expresión algebraica funciona para cualquier término de la sucesión? Compruébalo con el quinto término.
Si “n” toma el valor de cinco, entonces en lugar de “n” por dos más uno, se coloca (5 x 2) + 1, el resultado es once y efectivamente, el quinto término de la sucesión tiene once elementos.

Alumno 3:
El alumno 3 descompuso la secuencia en filas, y cada fila en subelementos que forman subfiguras, cuya cantidad depende de la posición que ocupa cada elemento dentro de la secuencia.
Él escribe: “Los cuadros de abajo son el número de la posición y arriba son el número de la posición más uno”. Esto permitió al estudiante organizar de manera adecuada la relación existente entre los elementos de la figura y lo llevó a generalizar con una expresión algebraica.
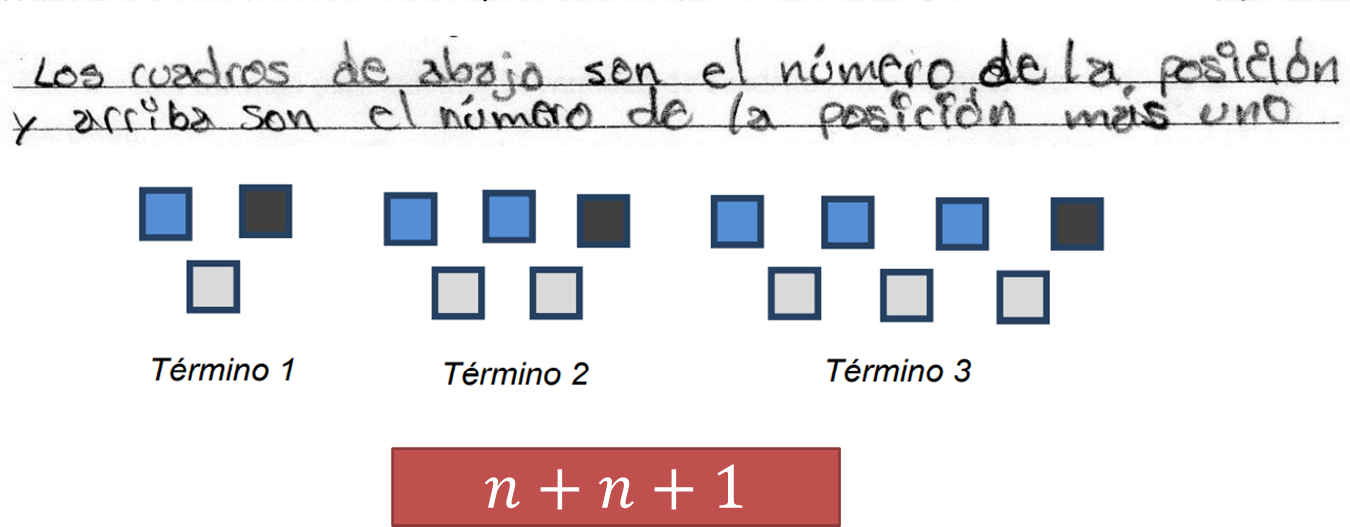
En este caso, el número de la posición se representa con “n” y, por lo tanto, el número de elementos que contiene la posición se puede encontrar con (n + n + 1). El primer término “n” representa el número que se asigna “a la posición” del término, y el término “n” más uno se refiere a “el número de la posición más uno”.
Así, se puede observar cómo es que los estudiantes pudieron conectar lo que vieron, con lo que escribieron con los símbolos algebraicos.
Analiza lo siguiente:
Esta última expresión es diferente a la que plantea la alumna 2. ¿Alguien está mal?
Para conocer lo anterior, revisa lo que plantea cada alumno y reflexiona al respecto.
La alumna 2 encuentra la expresión (n x 2 + 1), mientras que el alumno 3 plantea (n + n + 1). Si se cambia la variable “n” por el número diez ¿qué ocurre en cada caso?

Al resolver, empleando la jerarquía de operaciones, ambas expresiones llevan al mismo resultado. Por lo tanto, ambas son correctas.
Esto muestra que las dos formas son equivalentes, es decir, son dos expresiones algebraicas diferentes que formulan la misma situación. Entonces, es posible tener respuestas diferentes para la misma situación.
Cuando dos o más expresiones algebraicas generan la misma sucesión numérica se dice que las expresiones algebraicas son equivalentes, es decir, tienen el mismo valor.
A continuación, analiza el siguiente ejemplo.
2b = b + b
¿Qué piensas que pasaría si se cambia la letra “b” por el número 1? Toma un momento para reflexionar y después, observa qué sucede.
Al sustituir la letra “b” por el número 1, se obtiene la siguiente igualdad:
2 (1) = 1 + 1
Si se resuelven las operaciones, se obtiene que 2 es igual a 2. ¿Qué piensas que significa eso?, ¿pasará lo mismo si en lugar del número 1 se usa el número 2, el 3, el 8, o cualquier otro número?
Toma un momento para pensar y reflexionar, después, escribe una breve conclusión en tu cuaderno.
Ahora, el valor de la letra “b” será 8. Sustituye los valores en la igualdad.
2b = b + b
2 (8) = 8 + 8
16 = 16
Se obtiene que 16 es igual a 16.
De lo anterior se puede deducir que lo mismo pasará si se sustituye la letra “b” por cualquier número. Cuando sucede esto, se comprueba que las expresiones algebraicas son equivalentes.
Piensa en la siguiente cuestión:
¿Qué se puede hacer para encontrar una expresión equivalente a otra?
Para dar respuesta a la pregunta anterior, trabaja con la siguiente sucesión numérica que está parcialmente formada por los números:
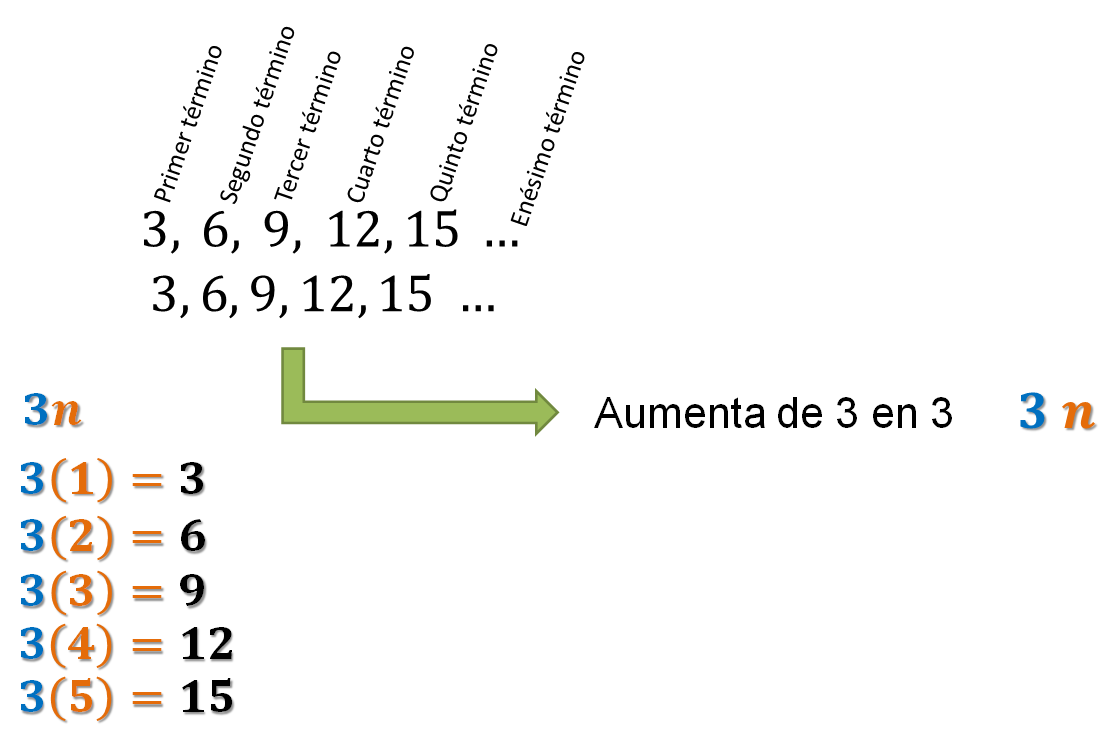
3, 6, 9, 12, 15…
Los puntos suspensivos indican que la sucesión no tiene fin, es decir, es infinita.
Ahora, encuentra la manera de saber cuál es la regla que genera una sucesión.
¿Conoces algún procedimiento para encontrar la regla general de una sucesión numérica? Describe tu procedimiento en tu cuaderno.
Para encontrar la regla general de una sucesión, se identifica la diferencia entre un término y su consecutivo. Asimismo, se observa si la diferencia es constante entre los demás términos.
¿Ya sabes cuál es la diferencia entre los términos de la sucesión anterior?
Como puedes notar, la sucesión numérica aumenta de tres en tres. Entonces, para escribir la regla general de esa sucesión, se anota el número 3, porque ya sabes que aumenta de tres en tres. Se relaciona con el número de término, es decir, con el número de posición. Como ese número es variable, se le asigna una literal, generalmente la letra “n”.
De tal manera, que la regla que genera la sucesión numérica es (3n). El 3 porque la sucesión va aumentando de tres en tres y la “n” para representar cualquier término de la sucesión.
Un método para encontrar expresiones algebraicas equivalentes a otra, consiste en descomponer una expresión algebraica en sus partes.
Ahora, debemos preguntarte:
¿Cómo puedes descomponer 3n en partes?
Para descomponer una expresión algebraica es muy importante saber leerlas y entender su significado. Si sabes eso, también puedes saber las partes de las que se compone cualquier expresión algebraica.
¿Cuál es el significado de 3n? 3n significa tres veces el valor de “n”. Entonces, ¿de cuántas partes se forma 3n? Piénsalo un momento.
La expresión algebraica 3n se forma de tres partes y sus partes son tres letras “n”. Ahora, debes pensar una forma diferente de unir esas partes, ¿tienes alguna idea de cómo hacerlo?
Se pueden unir esas letras a través de signos que indiquen una operación, en este caso, puede ser por medio de una suma, ya que, si se suma “n”, más “n”, más “n”, se tiene 3n; y con eso, ya se ha descompuesto la expresión algebraica; pero también existe otra expresión algebraica equivalente a 3n, que es 2n más “n”.

Ahora, encuentra por lo menos dos expresiones algebraicas equivalentes a:
6n + 4
Primero, observa cuáles son las partes que la forman. Si se separan todos los elementos queda de la siguiente forma:
n + n + n + n + n + n + 4
Incluso ese cuatro puede separarse en 1 + 1 + 1 +1
Con los elementos separados, ¿puedes escribir por lo menos dos expresiones equivalentes? Coméntalas y compáralas a distancia con tus compañeras y compañeros.
Ahora, analiza las siguientes expresiones y comprueba si son equivalentes:
2 (3n + 2)
2n + 2n + 2n + 4
Reflexiona:
¿Se parecen estas expresiones algebraicas a las que escribiste?
¿Cómo puedes comprobar que estas expresiones algebraicas son equivalentes?
Comprueba que las expresiones algebraicas anteriores son equivalentes a 6n + 4. Después, comprueba que las expresiones algebraicas que propusiste también sean equivalentes.
Una de las formas para comprobar la equivalencia de expresiones algebraicas consiste en resolver las operaciones algebraicas indicadas; otra es construir la sucesión numérica que representan. En esta sesión, construirás sucesiones numéricas para realizar las comprobaciones.
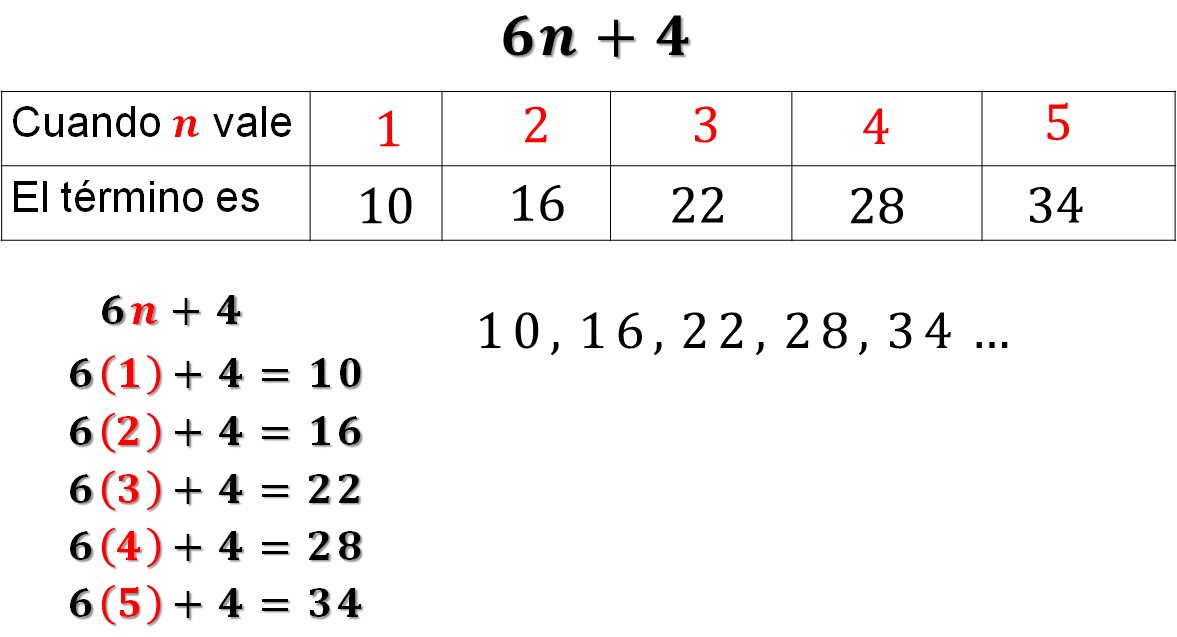
Primero construye la sucesión numérica que genera 6n + 4 Lo harás para los primeros 5 términos.
Lo que debes hacer es sustituir el valor de “n” por 1, pues como recordarás, “n” representa el valor del término que se está buscando, en este caso, representa el primer término de la sucesión. Por lo tanto, se tiene que:
6n + 4
6(1) + 4 = 10
Entonces se puede decir que cuando “n” vale 1, el término es 10
Ahora, calcula el segundo término. “n” vale 2 porque se está buscando el segundo término de la sucesión, Realiza los caculos:
6n + 4
6(2) + 4 = 16
Entonces podemos decir que cuando n vale 2, el término es 16
Para el tercer término “n” vale 3; entonces se tiene que:
6n + 4
6(3) + 4 = 22
Por lo tanto, se puede decir que cuando “n” vale 3, el término es 22
Para el cuarto término, “n” vale 4; entonces se tiene que:
6n + 4
6(4) + 4 = 28
Por lo tanto, se puede decir que cuando “n” vale 4, el término es 28
Para el quinto término, “n” vale 5; entonces se tiene que:
6n + 4
6(5) + 4 = 34
Por lo tanto, se puede decir que cuando “n” vale 5, el término es 34
Ya has terminado de calcular los primeros 5 términos de la sucesión. Eso quiere decir que la sucesión que genera la regla 6n + 4, está formada por los términos 10, 16, 22, 28 y 34. Observa como quedaron los resultados de esta expresión:
Al final se le agregan puntos suspensivos, ya que la sucesión continúa y no tiene fin.
Ahora ya sabes cuáles son los primeros términos de la sucesión. Para comprobar que las expresiones algebraicas que se escribieron son equivalentes a 6n + 4, sustituye “n” en las expresiones anteriores, por los números del uno al cinco. Si los resultados son idénticos, entonces la expresión algebraica es equivalente a 6n + 4.
Comienza con la expresión: 2 (3n + 2)
Se sabe que, para el primer término “n” vale 1. Sustituye y resuelve las operaciones paso a paso.
2 (3n + 2)
2 [3(1) + 2] = 2 [3 + 2] = 2 [5] = 10
Esto quiere decir que cuando “n” vale 1, el término es 10.
Para el segundo término “n” vale 2. Realiza la sustitución y resuelve las operaciones.
2 (3n + 2)
2 [3(2) + 2] = 2 [6 + 2] = 2 [8] = 16
Esto quiere decir que cuando “n” vale 2, el término es 16
Para el tercer término “n” vale 3
2 (3n + 2)
2 [3(3) + 2] = 2 [9 + 2] = 2 [11] = 22
Esto quiere decir que cuando “n” vale 3, el término es 22
Para el cuarto término “n” vale 4
2 (3n + 2)
2 [3(4) + 2] = 2 [12 + 2] = 2 [14] = 28
Esto quiere decir que cuando “n” vale 4, el término es 28
Para el quinto término “n” vale 5
2 (3n + 2)
2 [3(5) + 2] = 2 [15 + 2] = 2 [17] = 34
Esto quiere decir que cuando “n” vale 5, el término es 34
Ya has terminado de calcular los primeros 5 términos de la sucesión. Esto quiere decir que la sucesión que genera la regla “2 (3n + 2)”, está formada por los términos 10, 16, 22, 28 y 34. Observa como quedaron los resultados:

Como puedes observar, los términos de esta sucesión son idénticos a la sucesión anterior. Esto significa que ambas expresiones algebraicas son equivalentes.
Continua con la siguiente expresión: 2n + 2n + 2n + 4
Comprueba que esta expresión es equivalente a las dos expresiones algebraicas anteriores. Ya conoces el procedimiento para sustituir y resolver operaciones, así que esta vez te apoyaremos en el cálculo mental para avanzar más rápido.
Para “n” en el primer término se tiene que:
2n + 2n + 2n + 4
2(1) + 2(1) + 2(1) + 4 = 2 + 2 + 2 + 4 = 10
Para “n” en el segundo término se tiene que:
2n + 2n + 2n + 4
2(2) + 2(2) + 2(2) + 4 = 4 + 4 + 4 + 4 = 16
Para el tercer término se tiene que:
2n + 2n + 2n + 4
2(3) + 2(3) + 2(3) + 4 = 6 + 6 + 6 + 4 = 22
Para el cuarto término se tiene que: 2
2n + 2n + 2n + 4
2(4) + 2(4) + 2(4) + 4 = 8 + 8 + 8 + 4 = 28
En el quinto término se tiene que:
2n + 2n + 2n + 4
2(5) + 2(5) + 2(5) + 4 = 10 + 10 + 10 + 4 = 34
Al calcular los primeros 5 términos de la sucesión que genera la regla (2n + 2n + 2n + 4), se encuentra que está formada por los términos 10, 16, 22, 28 y 34. Observa como quedaron los resultados:

Los términos de esta sucesión son idénticos a los términos de las dos sucesiones anteriores. Entonces, las tres expresiones algebraicas son equivalentes.
Para finalizar, compara las siguientes expresiones. Sustituye el valor de “n” para comprobar si son equivalentes o no.
Expresión algebraica 1: 3 (n + 1)
Expresión algebraica 2: 5n + 1
Expresión algebraica 3: 3n + 3
En la primera expresión, sustituye “n” por 1 y 2:
3 (n + 1)
3 (1 + 1) = 3 (2) = 6
3 (2 + 1) = 3 (3) = 9
Al resolver, se obtiene el valor de 6 y 9, respectivamente.
En la segunda, también sustituye “n” por 1 y 2
5n + 1
5 (1) + 1 = 5 + 1 = 6
5 (2) + 1 = 10 + 1 = 11
Y en la tercera, sustituye de la misma manera a “n” por 1 y 2:
3n + 3
3 (1) + 3 = 3 + 3 = 6
3 (2) + 3 = 6 + 3 = 9
Cómo puedes observar, sí sólo se calcula el primer término de la sucesión en las expresiones algebraicas “3 (n + 1)”, “5n + 1” y “3n + 3”, parece que las expresiones son equivalentes, ya que, en los tres casos, se obtiene el mismo resultado.
Sin embargo, si se hace el cálculo con el segundo término de cada sucesión, puedes identificar que las tres expresiones algebraicas no son equivalentes entre sí.
¿Ya observaste que el valor del segundo término de la segunda expresión algebraica fue diferente? ¿Qué significa eso?
Esto significa que, solamente la primera y la tercera son equivalentes.
Por lo tanto, se puede concluir que: no basta con calcular un solo término para comprobar si dos o más expresiones algebraicas que generan una sucesión son equivalentes.
Con estos ejemplos aprendiste que se pueden identificar diferentes reglas que generan la misma sucesión numérica y a verificar su equivalencia con otras expresiones. Aunque sólo lo hiciste con la construcción de las secuencias numéricas que generan.
Hemos llegado al final de la sesión. Recuerda que este es un material de apoyo. Para complementar lo estudiado puedes consultar otras fuentes, como tu libro de texto de matemáticas de segundo grado.
El reto de hoy:
Escribe expresiones equivalentes de los ejemplos que se mencionaron en esta sesión. Además, resuelve los ejercicios de tu libro de texto de Matemáticas, correspondientes a este tema. Finalmente, coméntalas y compáralas a distancia con tus compañeras y compañeros.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas