Calculando (x + a) (x + b)
Calculando (x + a) (x + b)
Aprendizaje esperado: resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: calcular expresiones de la forma (x + a) (x + b).
¿Qué vamos a aprender?
Aprenderás a calcular expresiones de la forma (x + a) (x + b). Lo que vas a necesitar para esta clase serán cuaderno, lápiz y goma.
Anota las dudas, inquietudes o conclusiones que surjan al resolver los planteamientos dados en esta lección.
Seguramente en alguna ocasión resolviste binomios en tu clase de Matemáticas.
Dentro del álgebra y la multiplicación de polinomios se tiene a un grupo de operaciones que se les llama “productos notables”. Para que reciban este nombre, se emplea una regla para abreviar el procedimiento y desarrollar el cálculo mental al resolverlos.
Una de estas reglas es la de los dos binomios con elementos iguales que reciben el nombre de binomio al cuadrado. Es el más conocido, pues su representación geométrica es la figura de un cuadrado.
¿Qué hacemos?
Trabaja el producto de dos binomios de la forma (x + a) por (x + b), observa a qué hace referencia mediante el siguiente ejemplo.
Una persona va a adquirir un salón de baile. Las medidas del local son 14 metros de frente y 15 metros de fondo.
Esta persona lo comprará siempre y cuando pueda distribuir el espacio de la siguiente manera:
– Un cuadrado cubierto de duela para pista de baile.
– En contraesquina de esta pista debe estar localizada la orquesta.
– Y dos secciones a la orilla de la pista para la zona de las mesas de al menos 80 metros cuadrados.
El esquema que tiene en mente es el siguiente:
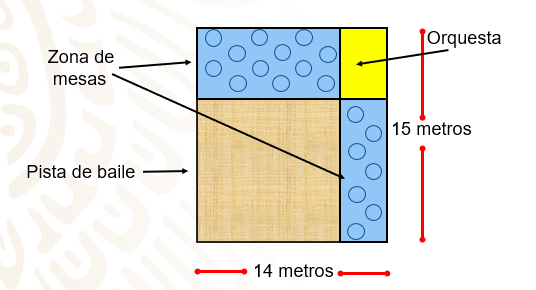
Como puedes observar en el rectángulo que representa el salón, se tienen 4 secciones: un cuadrado y tres rectángulos menores de distintas áreas.
El dueño se da cuenta de que su presupuesto para la duela de la pista de baile alcanza para cubrir 100 metros cuadrados, así que de esa medida será la pista de baile.
Con base en ello se pregunta: ¿cuál es el área que ocupará la orquesta?, ¿alcanzará para tener al menos 80 metros cuadrados para las mesas?
Observa qué debe hacer.
Debido a que quiere en forma de cuadrado la pista de baile, y son 100 metros cuadrados de duela, la longitud de ese cuadrado debe ser de 10 metros por lado, el resto de las secciones quedará necesariamente de la siguiente forma:
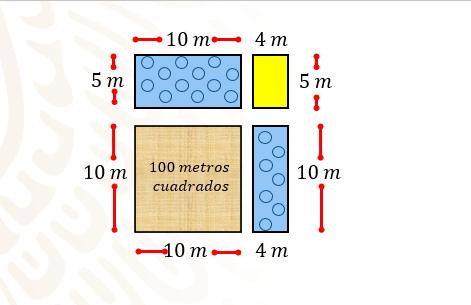
Al tener un cuadrado de lado 10 para la pista, y el salón de baile mide 15 metros de fondo, quedan 5 metros disponibles.
En el frente le quedan entonces 4 metros libres, por lo que se forman dos rectángulos, uno de 5 por 10 metros y otro de 4 por 10 metros, y observando te das cuenta de que en el esquema queda delimitada la zona para la orquesta.
Esta zona medirá entonces 5 por 4 metros. Entonces, sólo falta calcular las áreas restantes de las zonas de orquesta y las mesas, y con ello podrás saber si es el lugar que está buscando.
Calcula:
La pista de baile tiene 100 metros cuadrados. En el rectángulo de 5 por 10 metros tiene un área de 50 metros cuadrados. En otro rectángulo de 4 por 10 metros tiene un área de 40 metros cuadrados. Y en la zona restante tiene un rectángulo de 4 por 5 metros, lo que da 20 metros cuadrados.
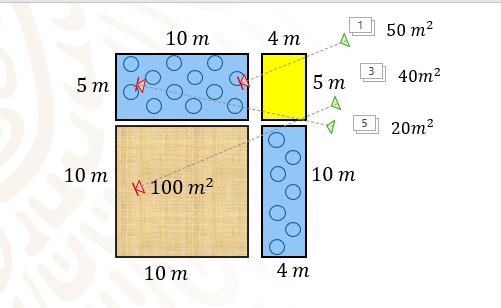
Entonces, si tiene dos rectángulos para la zona de mesas de 50 y 40 metros cuadrados cada una, se dispone de 90 metros cuadrados para la zona de mesas y eso es más de lo que necesitaba como mínimo, por lo que sí cumple con las condiciones que estableció para su compra.
Pero ¿cómo se relaciona este ejemplo con el propósito de la sesión?, ¿Qué sucede si a esta representación geométrica le das el valor de “x” al lado del cuadrado que se tenía en 100 metros cuadrados?, ¿Qué pasa con las áreas de las 4 secciones que se forman? Observa el esquema.
Tienes ahora que las dimensiones de frente y fondo del rectángulo están representadas por “x” más 4 y por “x” más 5. Entonces las áreas de las 4 secciones quedan del siguiente modo:
- El cuadrado de lado “x” tiene área de “x” cuadrada.
- El rectángulo de base 4 y altura “x” tiene un área de 4x.
- El rectángulo de base “x” y altura 5 tiene un área de 5x.
- Y el área del rectángulo restante es de 4 por 5 igual a 20.
Con las literales te das cuenta de que la base y la altura del rectángulo tienen el formato de binomios (x + a) y (x + b).
En donde “a” y “b” representan dos cantidades distintas entre sí, mientras que “x” es lo que se le llama un término común.
Los binomios de la forma (x + a) por (x + b) tienen un término común —que en este caso es la “x”—, y un término que es diferente en ambos binomios.
Utiliza la representación geométrica para resolver otro ejemplo, observa la representación geométrica del producto (x + 3) por (x + 4).
Forma una figura cuya base sea el primer binomio (x + 3) y de altura sea (x + 4).
Como se trata de un rectángulo, añades las secciones que corresponden. Así, se forma un cuadrado de lado “x” y se añaden en la base 3 rectángulos de base 1 y de altura “x”.
En la parte que falta de la altura se añaden 4 rectángulos de altura 1 y de base “x”.
Para completar la figura rectangular, añades las piezas unitarias necesarias, esto es que agregas piezas de lado 1 hasta completarlo. Se requiere que formes un rectángulo de lados 3 por 4. El resultado es de 12 unidades.
Pero ¿cómo se obtiene el área total de la figura? Si sumas el área de todas las piezas que lo conforman, puedes obtener el área total, aunque no todas son del mismo tipo.
Cuenta las áreas que son del mismo tipo. Tienes:
- 1 cuadrado de área “x” cuadrada.
- 4 más 3 piezas de área “x”.
- Y 12 piezas de área 1.
Así se representa la suma algebraica de los términos: “x” cuadrada más 7 “x” más 12. Ese es el resultado algebraico.
Y como la figura es un rectángulo, su área se obtiene multiplicando la base por la altura.
Entonces, x cuadrada más “7x” más 12 es el resultado de la multiplicación de (x + 3) por (x + 4).
Observa el procedimiento algebraico.
Tienes (x + 3) por (x + 4).
Multiplicas “x” por “x” y obtienes “x” cuadrada.
Multiplicas “x” por 4 y obtienes “4x”.
Multiplicas 3 por “x”, que es igual a “3x”.
Multiplicas 3 por 4 y obtienes 12.
Reduce términos semejantes y te queda “x” cuadrada más “7x”, más 12.
De este modo, resuelves algebraicamente. En este caso, la regla que te servirá para abreviar el procedimiento.
Observa otro ejemplo:
Tienes ahora las siguientes piezas:
- 1 de “x” cuadrada,
- 6 piezas de área “x”
- y 8 piezas unitarias.
Forma el rectángulo correspondiente. Ahora, con las piezas en su lugar, puedes ver que la base es “x” más 4 y la altura es “x” más 2.
¿Y cuál es el área total?
El área total es “x” cuadrada más “6x”, más 8, entonces el producto de (x + 4) por (x + 2) es igual a “x al cuadrado” más “6x”, más 8.
No siempre se tiene una sola pieza de “x” cuadrada pueden ser más piezas.
Observa otro ejemplo.
Forma ahora un rectángulo cuya base debe medir “2x” más 1 y de altura 2x más 2.
Ahora coloca las piezas necesarias para lograr formar el rectángulo.
Inicia colocando dos piezas de “x” cuadrada en la base. Después, como debe tener dos piezas de “x” cuadrada de altura, ajusta las piezas necesarias.
Deben ser 4 piezas de “x” cuadrada.
Efectivamente, debes formar un cuadrado con las piezas de área “x” al cuadrado. Añade ahora en la base una pieza de base 1 y altura “x”. Para completar la altura del rectángulo, añades dos piezas de base “x” y altura 1.
Ahora añade más piezas de área “x”, para ajustar el espacio de las piezas de “x” cuadrada, necesarias para formar el rectángulo.
Debes añadir varias piezas más del área “x”, tanto en horizontal como en vertical, para completar las piezas que rodean las 4 piezas de “x” cuadrada.
Efectivamente, se completan hasta ser 6 piezas. Finalmente, añades las piezas de área 1 que en total son 2. Así, el área del rectángulo es igual a “4x cuadrada” más “6x”, más 2.
Entonces, el producto de (2x + 1) por (2x + 2) es igual a “4x cuadrada” más “6x”, más “2”.
Ahora debes trabajar la parte algebraica para lograr encontrar la regla que te permita abreviar el procedimiento de este producto de binomios con término común.
Considera los 3 ejemplos que has realizado, apoyándote en su representación geométrica. Los ejemplos son:
- (x + 3) por (x + 4)
- (x + 4) por (x + 2)
- (2x + 1) por (2x + 2)
Tienes los resultados que se obtuvieron de cada uno de ellos. Analiza si encuentras una regularidad.
Se puede observar que en todos ellos se formó un cuadrado con las piezas que corresponden al término común del binomio.
Y con las piezas de área “x” se puede ver que en las dos primeras tienes una cantidad igual a la suma de los términos no comunes: en la primera son 7 piezas de “x”, que es la suma de 3 más 4. En la segunda son 6 piezas de “x”, que es la suma de 4 más 2. Pero en el tercer ejemplo no se encuentra eso mismo. Deberían ser sólo 3 y se tiene 6.
Ese análisis es correcto, pero falta observar con más detalle.
En el tercer ejemplo son 6 piezas de “x” porque se ven afectadas al tener no sólo una “x” cuadrada en la base y en la altura del rectángulo. Observa: esa parte hace que exista un cambio.
Como no tienes dos piezas de “x” cuadrada en los binomios, las piezas de área “x” son el doble de la suma que se había contemplado.
Las piezas unitarias corresponden al producto que se obtiene de multiplicar los términos no semejantes:
- 3 por 4 son 12 en el primer ejemplo,
- 4 por 2 son 8 para el segundo y
- 1 por 2 igual a 2 para el tercer ejemplo.
Resumiendo, se tiene que el producto de dos binomios con término común es igual a elevar al cuadrado el término común más la suma de los términos no comunes multiplicándolos por el común, más el producto de los términos no comunes.
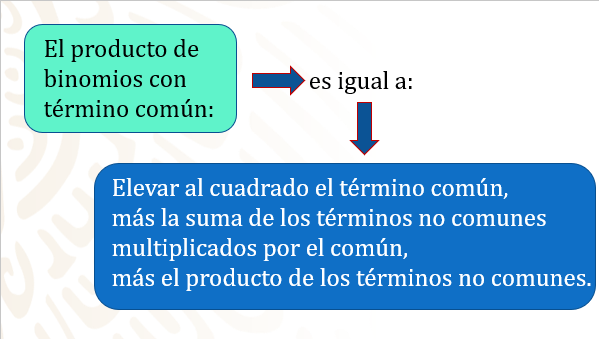
Observa sólo las expresiones algebraicas anteriores:
Tienes (x + 3) por (x + 4). Si aplicas lo antes descrito, tienes “x”, que es el término común, y 3 y 4 que son los términos no comunes. Así, el cuadrado del común es “x” cuadrada.
Se suman 3 y 4, y obtienes 7. Este 7 lo multiplicas por “x”, que es el común, y tienes 7x. Finalmente multiplicas 3 por 4 y es 12.
En el ejemplo 2 tienes: (x + 4) por (x + 2).
Se aplica el cuadrado del término común, que es “x cuadrada”. Se suman 4 más 2 y se multiplica por “x”, se tiene “6x” y multiplicas 4 por 2; resulta en 8.
En el último ejemplo: (2x + 1) (2x + 2). Aplicando, se tiene el cuadrado de “2x”, que es “4x” cuadrada. Se suma 1 más 2, que es 3, lo multiplicas por “2x”, que es el común, y se obtiene “6x”. Por último, se multiplica 1 por 2, igual a 2
Y obtienes los resultados directamente.
Ahora realiza otro ejercicio, completa las áreas que se forman en el siguiente esquema y verifica que el resultado sea correcto.
Ahora el esquema ya no lleva piezas individuales de “x” y de 1, pero se aplicará lo que acabas de aprender.
Como la base es (x + 5) y la altura es (x + 3), tienes que la zona verde es “x cuadrada” porque es el cuadrado del término común.
La zona de color amarillo es “8x”, ya que es la suma de “5x” y “3x”, que corresponden a la suma de los términos no comunes multiplicados por “x”, el común.
¿A qué es igual el producto de “x” más 5 por “x” más 3?
Sumando todos los anteriores términos, es igual a “x cuadrada” más “8x”, más 15. También, puede haber cantidades negativas en esos binomios, los binomios pueden representar una sustracción.
Observa un ejemplo con los modelos geométricos.
Realiza la multiplicación de (x + 2) por (x – 4).
Para ello, formarás diversas secciones: inicia colocando el cuadrado que representa a “x” cuadrada, que es cuadrado del término común.
A continuación, añades una sección que representa al dos del primer binomio, que es un rectángulo de área 2x.
Posteriormente representas la sustracción que está en el siguiente binomio “x” menos 4.
Para ello, debes reducir la altura, que es “x”, en una franja de ancho 4, que abarca todo el largo de la figura representada por este rectángulo de fondo blanco.
Has representado esta franja con una sección achurada para que puedas ver que disminuye a la sección de “x” cuadrada, y una sección completamente blanca, que disminuye la zona de color amarillo que representa a 2x.
De este modo, esta franja que representa la disminución de 4 unidades a “x”, reduce el área que se tenía inicialmente, que es “x” cuadrada más 2x (zona roja y zona amarilla).
Finalmente, observa qué parte es la que corresponde a la sección que se disminuye. Es un rectángulo que en la zona achurada tiene un área de 4x, y en la zona blanca, 8, pues al ser rectángulos, se obtiene su área multiplicando su base y su altura.
Así, (x + 2) por (x – 4) es igual a “x” cuadrada más 2x, menos 4x, menos 8.
Al reducir términos semejantes, es igual a “x” cuadrada menos 2x, menos 8.
Se observa que también la sustracción se puede representar en estos modelos geométricos. Es cuestión de analizar con cuidado las representaciones que se pueden obtener.
Resuelve: Multiplicar (x + 2) por (x – 4) es igual al cuadrado de “x”, que es “x cuadrada”. Se suman los términos no comunes, que en este caso son 2 y 4 negativo, obtienes 2 negativo y lo multiplicas por “x”. Así queda “2x negativo” y, por último, multiplicas 2 por “4 negativo” y obtienes “8 negativo”. Se obtiene lo mismo que con las figuras.
Por último, se te reitera la regla que se obtuvo durante la sesión.
Para multiplicar binomios con término común, elevas al cuadrado el término común. Se suman los términos no comunes y los multiplicas por el común, y multiplicas los términos no comunes y sumas esos tres términos.
El reto de hoy:
Se te recomienda completar tus notas sobre este tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas









