Información en encuestas y muestreo
Información en encuestas y muestreo
Aprendizaje esperado: calcula y explica el significado del rango y la desviación media.
Énfasis: fortalecer el estudio con información obtenida en encuestas y muestreos.
¿Qué vamos a aprender?
Los materiales que vas a utilizar son tu cuaderno de apuntes, lápiz, goma.
En medida de lo posible, te sugerimos tomar nota de cada una de las dudas que surjan durante el desarrollo de la sesión para que puedas compartirlas con tus compañeros y profesores.
Ya sabes lo que es una encuesta, las características y aplicación del muestreo, las medidas de tendencia central: moda, mediana y media aritmética.
En esta sesión consolidarás algunos conceptos sobre estudios estadísticos, como encuesta y muestra.
¿Qué hacemos?
Observa algunos conceptos, como la encuesta. La encuesta es una técnica empleada en la investigación para obtener datos y analizarlos; asimismo, es diseñada con un propósito, se identifica a qué población o muestra va destinada, se plantean preguntas específicas y concretas para llegar al objetivo.
Lo primero que debes de tomar en cuenta para diseñar una encuesta es identificar a qué población va ir destinada.
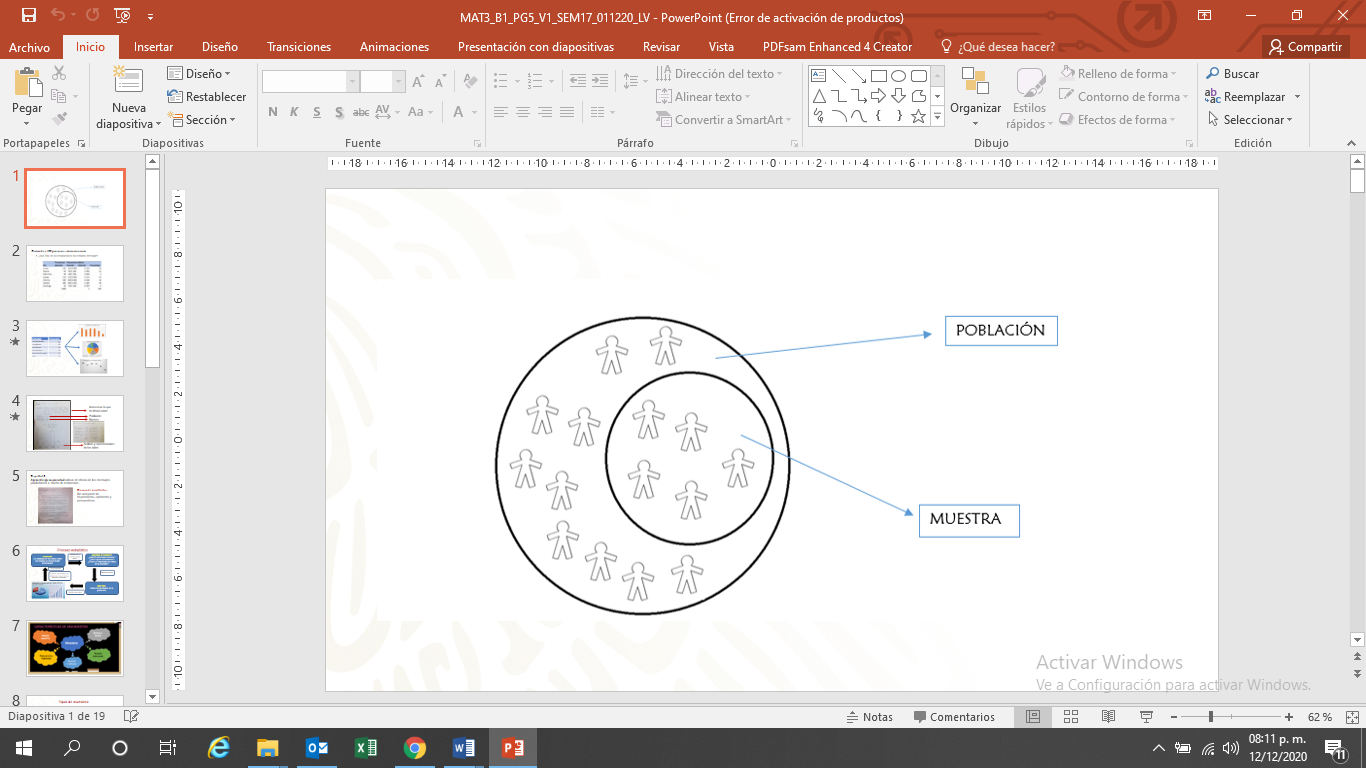
Se le llama “población” a un conjunto de individuos o un conjunto de elementos que presentan características comunes.
Una muestra se refiere a una parte de la población; esto es, en caso de que no te sea posible encuestar a todos los miembros de ésta, puedes encuestar a un porcentaje.
Así, una muestra es un conjunto representativo de la población en un estudio estadístico. Es decir, el número de personas es menor al de una población.
En general, los datos que se obtienen en un estudio o experimento estadístico pueden ser de dos tipos: cualitativos o cuantitativos.
Los datos cualitativos son, por ejemplo, el color de cabello, ojos o piel, y cuantitativos son, por ejemplo, la edad, el peso y la estatura de una persona.
En ambos casos se pueden organizar en tablas de frecuencia absoluta, relativa o porcentaje.
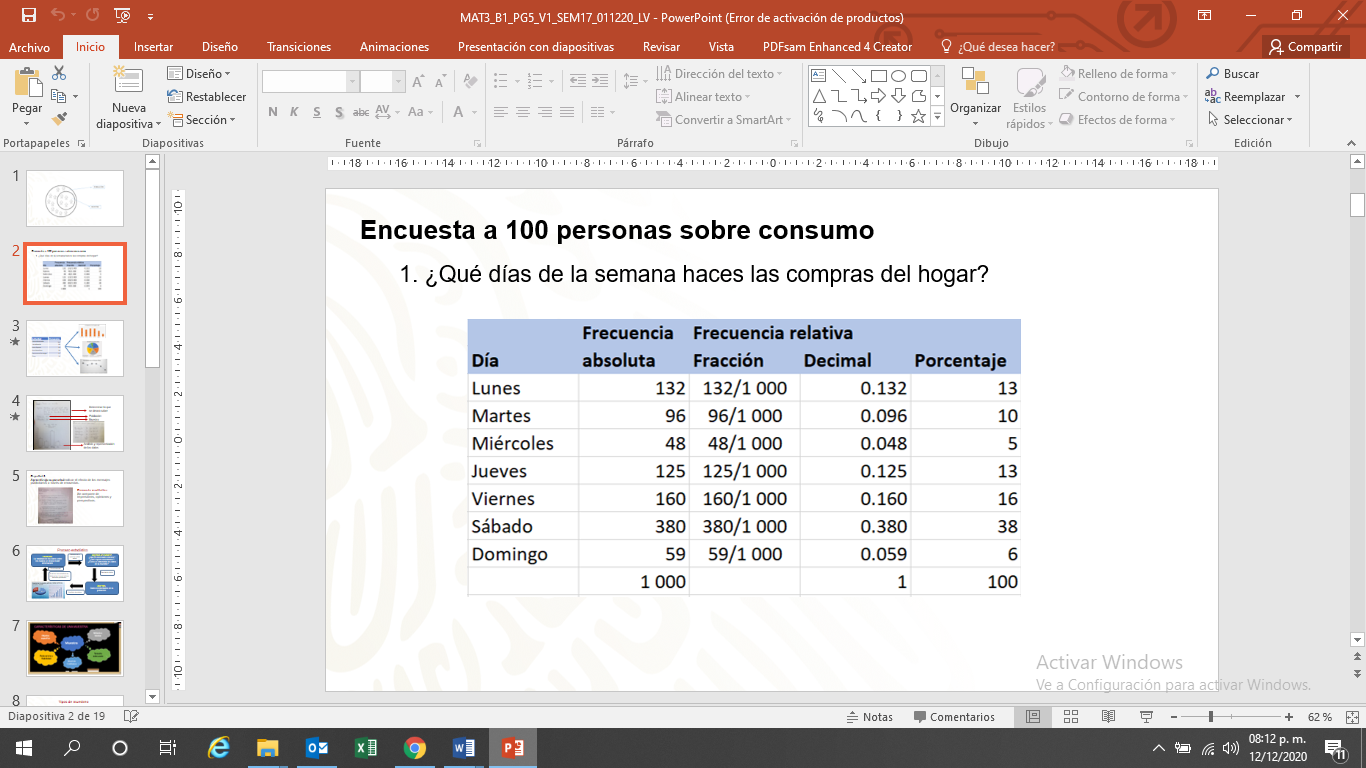
Cuando el conjunto de datos es cuantitativo y grande, se puede organizar en tablas de datos agrupados en intervalos.
Para representar los datos del resultado de la encuesta es importante realizarlo mediante gráficas; éstas pueden ser:
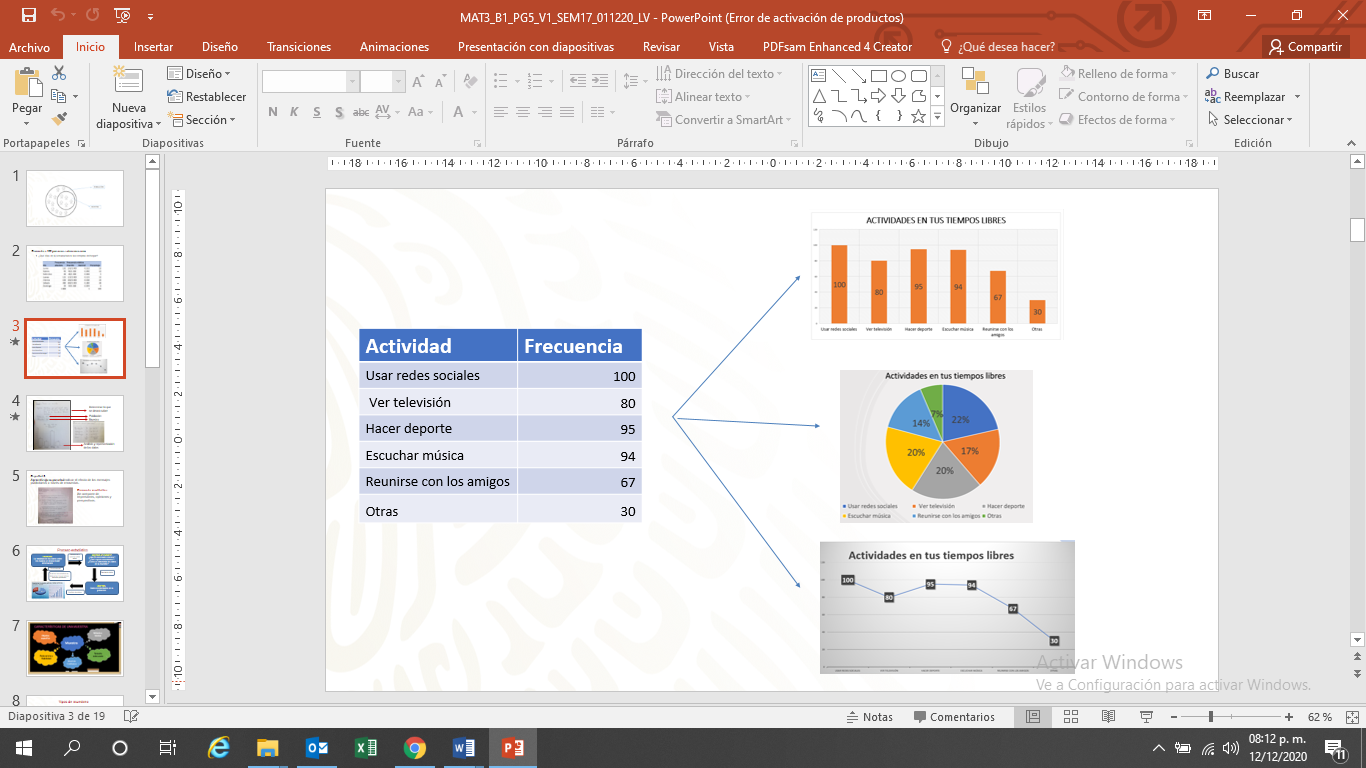
- Gráfica de barras, que se utiliza para presentar y comparar frecuencias con que ocurre una cualidad o atributo.
- Circular, sirve para comparar qué fracción de un todo es cada parte.
- Gráfica histograma, que presenta datos agrupados en intervalos; cuando éstos son iguales, la altura de cada barra indica su frecuencia.
- Gráfica de un polígono de frecuencias, que también muestra la frecuencia absoluta, relativa o porcentaje de datos agrupados.
Lo importante es utilizar la gráfica que mejor represente tus datos.
Revisarás algunos retos que realizaron alumnos de secundaria de tercer grado, referentes al aprendizaje esperado.
Diseñar una encuesta de un tema de tu interés y presentar los datos organizados, eligiendo la gráfica que mejor se adapte para representar la información, es algo que hizo Julieta, de Zumpango, Estado de México.
Si observas en la evidencia de su actividad, determinó el objetivo de su encuesta. Ya sabes que el objetivo consiste en definir qué aspecto de la población se va a investigar y, con base en esto, elaborar el instrumento a emplear.
También observas que identificó a la población o la muestra y, finalmente, seleccionó una gráfica de barras para representar los resultados.
Julieta lo que quería obtener de su encuesta fue identificar qué red social usan con mayor frecuencia los alumnos de 3.º D de su secundaria.
La población es de 45 y la muestra es 30 alumnos; es decir, del total del grupo sólo se aplicó la encuesta a 30 alumnos.
La pregunta que les realizó a sus compañeros fue: ¿cuál red social usas más?
Como puedes observar, ella realizó una gráfica de barras para representar los resultados.
Las encuestas que son cortas, directas al punto y son lo más claras posible, resultarán más precisas; sin embargo, para elaborar el número de preguntas debes asegurarte de haber pensado en el objetivo al que deseas llegar.
Las preguntas no deben ser engañosas o confusas, si quieres obtener buenos resultados, debes tener cuidado en el planteamiento de las preguntas.
¿Qué tipo de datos arrojó la encuesta de Julieta? Cuantitativos.
La muestra es representativa del grupo ya que representa más de 50% de la población, es decir, fueron 30 encuestados de 45.
Con la gráfica circular pudo representar esos datos, pues también obtuvo el porcentaje de lo que representa cada respuesta.
Rogelio, de Tula, Tamaulipas, escribió que él y sus compañeros pensaron en qué otras áreas del conocimiento se pueden emplear las encuestas como parte de un estudio estadístico, y lo acaban de usar en un proyecto de la asignatura de Español de tercer grado, ya que analizaron el efecto de los mensajes publicitarios a través de encuestas; de hecho, envió una fotografía de su proyecto de Español.
Si observas, la encuesta de Rogelio es cualitativa porque se compone de impresiones, opiniones y perspectivas. Este tipo de encuestas aportan un conocimiento profundo a partir de las preguntas de investigación, pero sus resultados son a veces difíciles de analizar y representar.
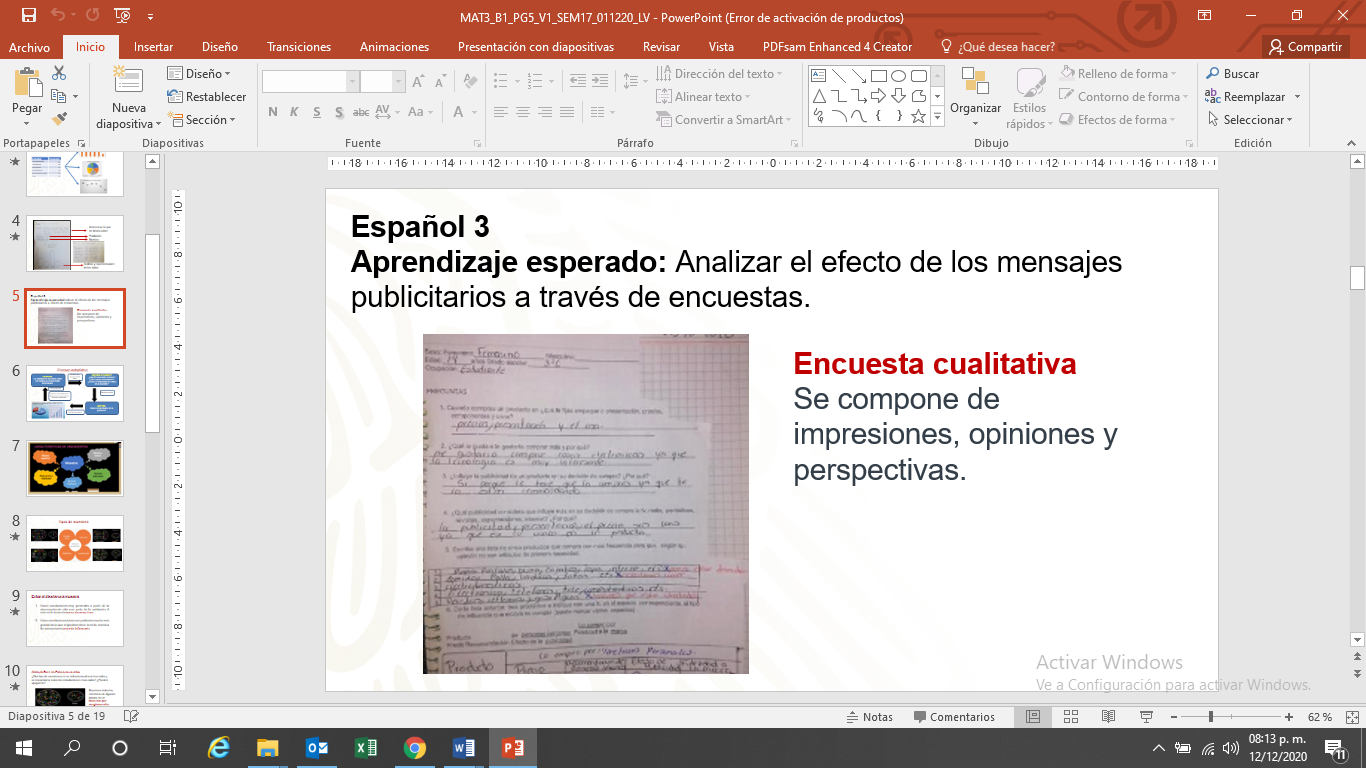
Con respecto a que es más conveniente usar, si datos cuantitativos o cualitativos, eso va a depender del objetivo que buscas, pero los datos cuantitativos pueden ayudarte a observar el panorama general. En cambio, los datos cualitativos brindan información detallada y aportan una voz personal a los resultados de tu encuesta.
¿qué debes hacer cuando quieres realizar un estudio sobre algún asunto?
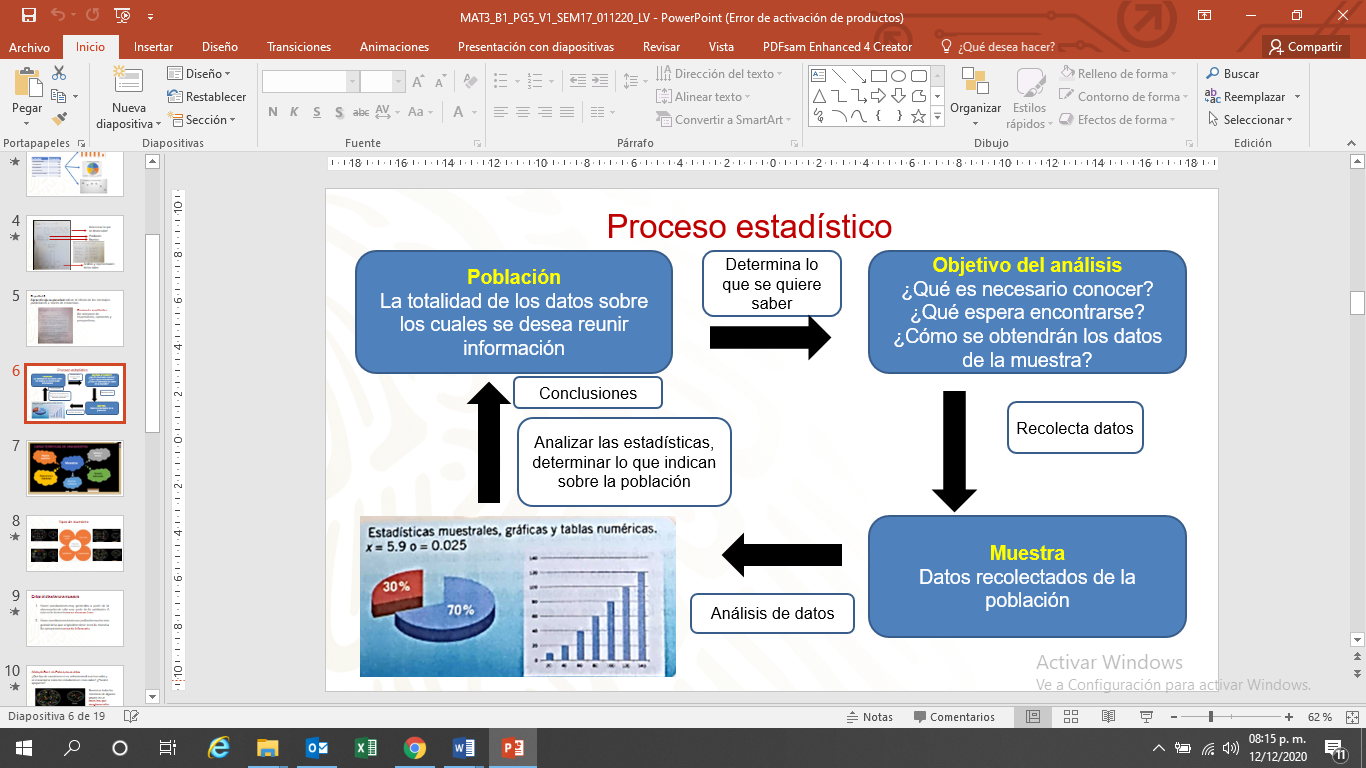
- Determinar qué grupo o población deberá ser considerado para realizar el estudio.
- Elaborar la encuesta que utilizarán para recopilar los datos en tu cuaderno. Debes reflexionar sobre el tipo de preguntas que se plantearán y las posibles respuestas que se obtendrán.
- Aplicar la encuesta y clasificar las respuestas obtenidas.
- Considerar, además, ¿qué tipo de representación gráfica y tabular utilizarás?
- Obtener y verificar las conclusiones a las que se llega.
Ahora, te centrarás en el muestreo. El muestreo es una técnica estadística en la que se revisa un subconjunto de una población de estudio y tiene como principal propiedad que es representativo del total, o sea, de la población considerada.
El muestreo es el procedimiento que se emplea para extraer una pequeña parte de una población de estudio dentro de un universo o población.
La muestra debe lograr una representación adecuada de la población en la que se reproduzcan de la mejor manera los rasgos esenciales que son importantes para el trabajo. Para que una muestra sea representativa y, por lo tanto, útil, debe reflejar las similitudes y diferencias encontradas en la población, es decir, ejemplificar las características de ésta.
Las características del muestreo son:
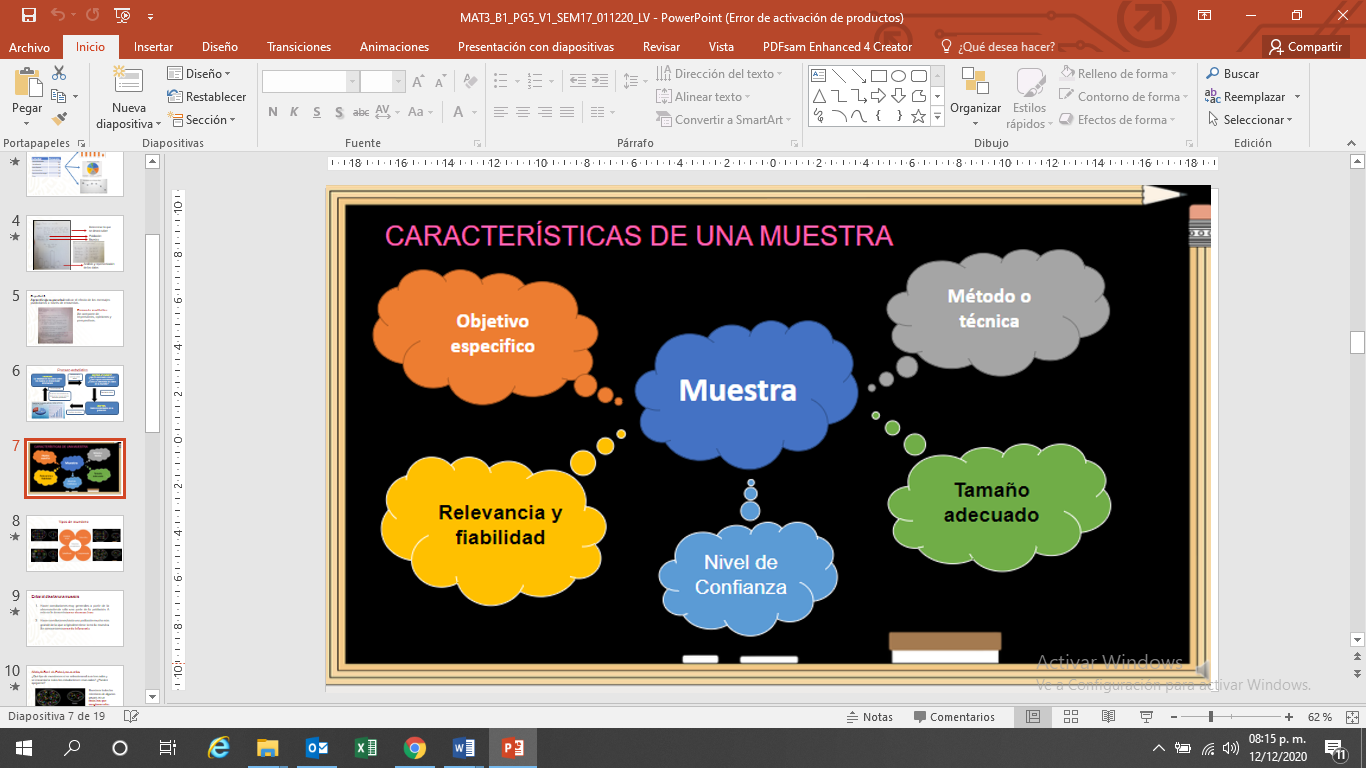
- Se debe considerar el objetivo específico que se ha de lograr.
- La combinación de procedimientos que tienen mayor posibilidad de alcanzar dicho objetivo, es decir, el método o la técnica a utilizar.
- La relevancia y fiabilidad de la información que se utilizará.
- La elección de un tamaño adecuado de la muestra con precisión, es decir, el margen de error, y un nivel de confianza aceptable.
Existen cuatro tipos de muestreo:
- Aleatorio simple
- Estratificado
- Sistemático
- Conglomerado
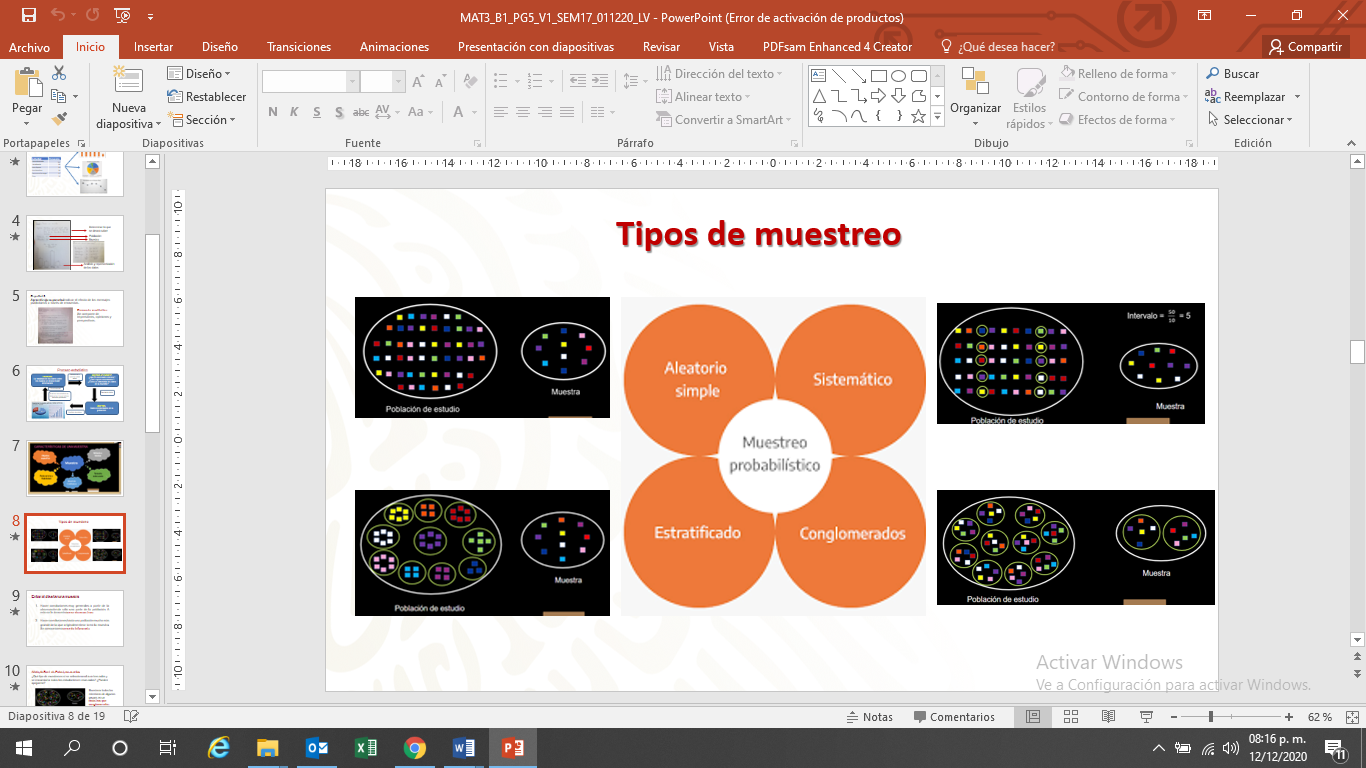
Estos muestreos consisten en:
Muestreo aleatorio simple: todos tienen la misma posibilidad de ser elegidos.
Muestreo estratificado: se pretende asegurar la representación de cada grupo.
Muestreo sistemático: se elige al azar un elemento a partir de él, cada intervalo se elige a quien será parte de la muestra.
Muestreo conglomerado: se tienen varios grupos homogéneos y se eligen grupos completos al azar.
Debes evitar, al estudiar una muestra, dos situaciones:

Se puede saber con certeza cuando una muestra es representativa o no.
Hay dos criterios que permiten tomar decisiones para mejorar la representatividad de una muestra:
- Una muestra más grande generalmente es más representativa que otra más pequeña.
- Una muestra aleatoria, es decir, elegida al azar, de manera que cualquier miembro de la población tenga la misma probabilidad de quedar en la muestra; generalmente es más representativa que otra que no haya sido elegida al azar.
Las muestras aleatorias son las que se utilizan en los análisis estadísticos.
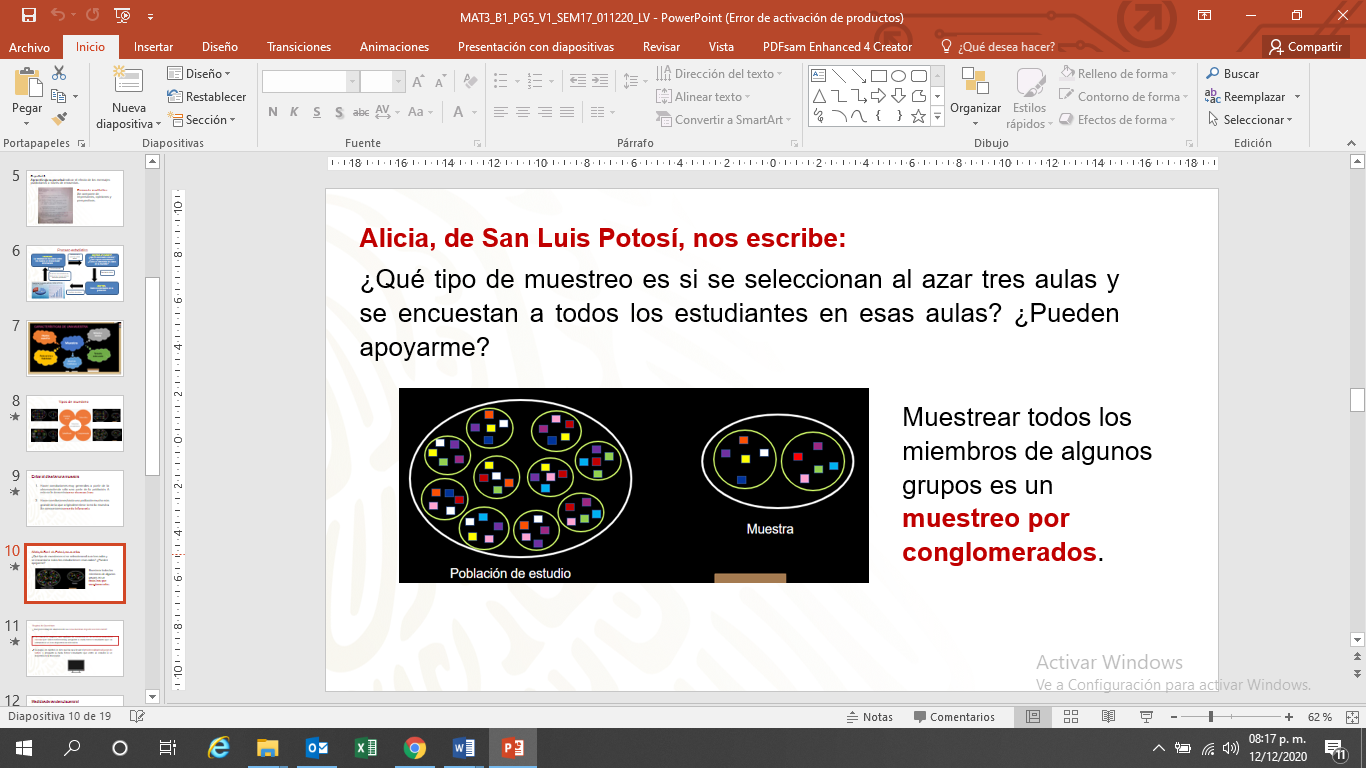
Los alumnos se separan en grupos (aulas) y se eligen algunos de esos grupos aleatoriamente. Todos los miembros de los grupos seleccionados están en la muestra.
Muestrear todos los miembros de algunos grupos es un muestreo por conglomerados.
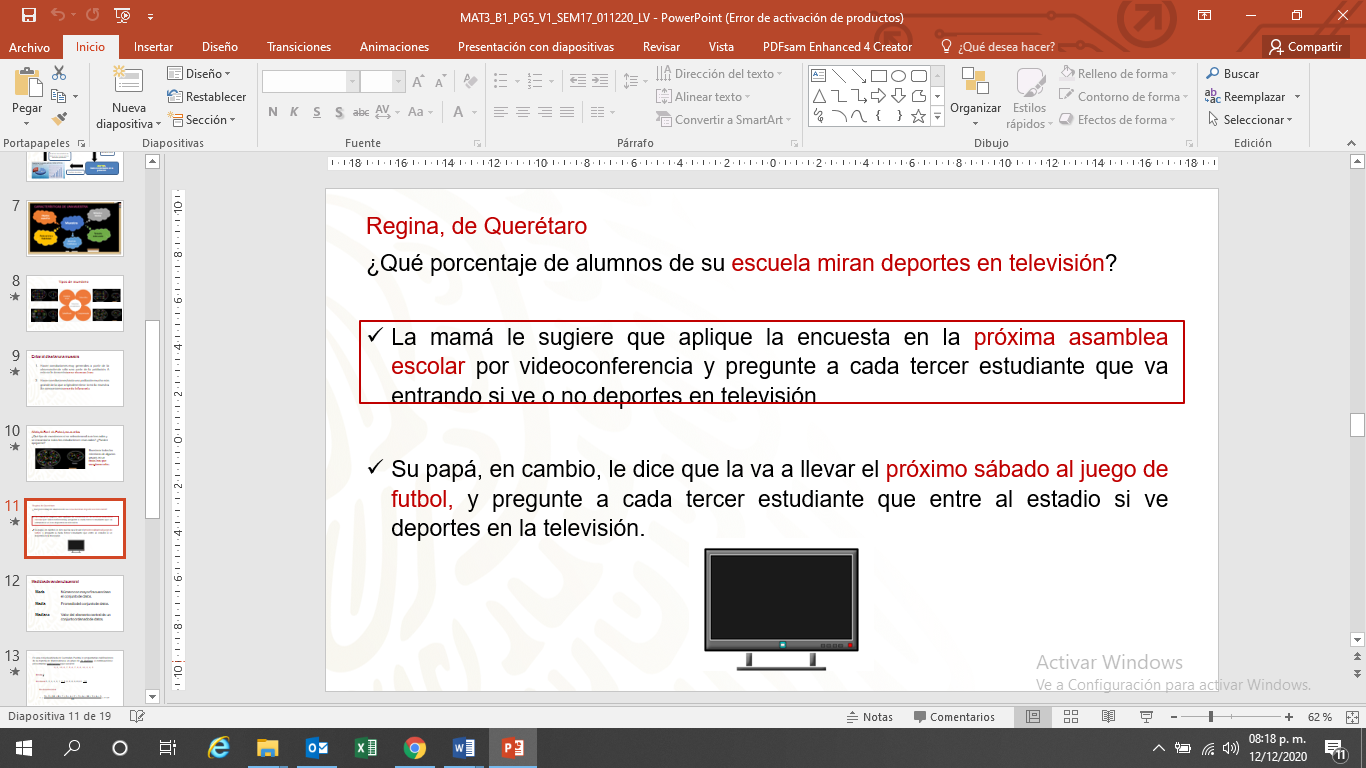
Ayuda a Regina a saber cuál estrategia de muestreo será más probable que genere una muestra representativa.
A los estudiantes en un partido de futbol les puede gustar más ver deportes que a los estudiantes que no van a los partidos.
Si Regina quiere saber sobre los estudiantes en su escuela, debe realizar una muestra de tal manera que cada estudiante de su escuela tenga la misma probabilidad de estar en la muestra.
La respuesta para una muestra más representativa es la que sugiere su mamá.
En la asamblea escolar por videoconferencia preguntar a cada tercer estudiante que va entrando si ve o no deportes en televisión.
Repasa las medidas de tendencia central, estas son medidas estadísticas que pretenden resumir en un solo valor a un conjunto de valores.
Las medidas de tendencia central más utilizadas son media, mediana y moda.
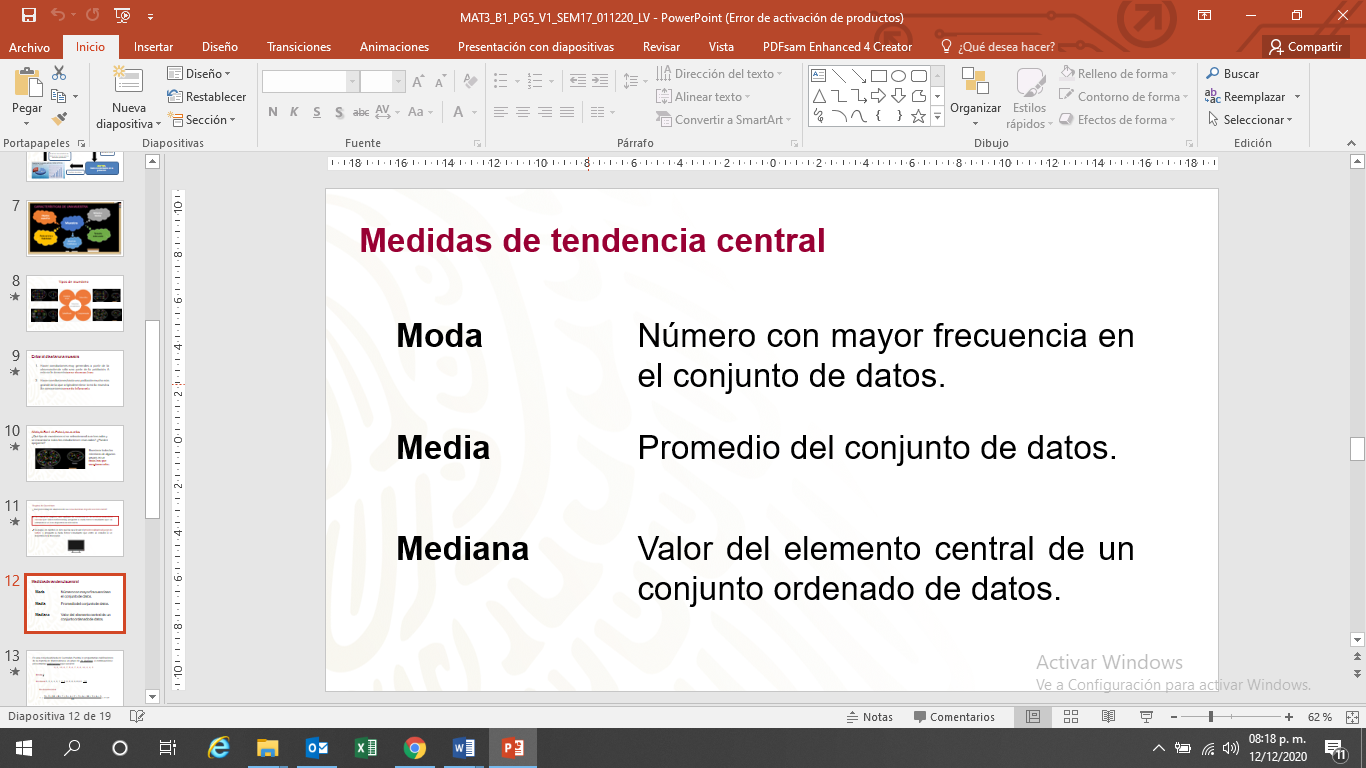
La moda es el dato que más se repite.
La media aritmética es el valor promedio de un conjunto de datos numéricos, calculada como la suma del conjunto de valores dividida entre el número total de valores.
La mediana representa el valor de la variable de posición central en un conjunto de datos ordenados.
¿Se pueden obtener las medidas de tendencia central en una encuesta cualitativa? De las tres que se mencionaron, sólo es posible la moda.
Las medidas de tendencia central recurrentemente son usadas para datos cuantitativos.
Observa un ejemplo para recordarlo.
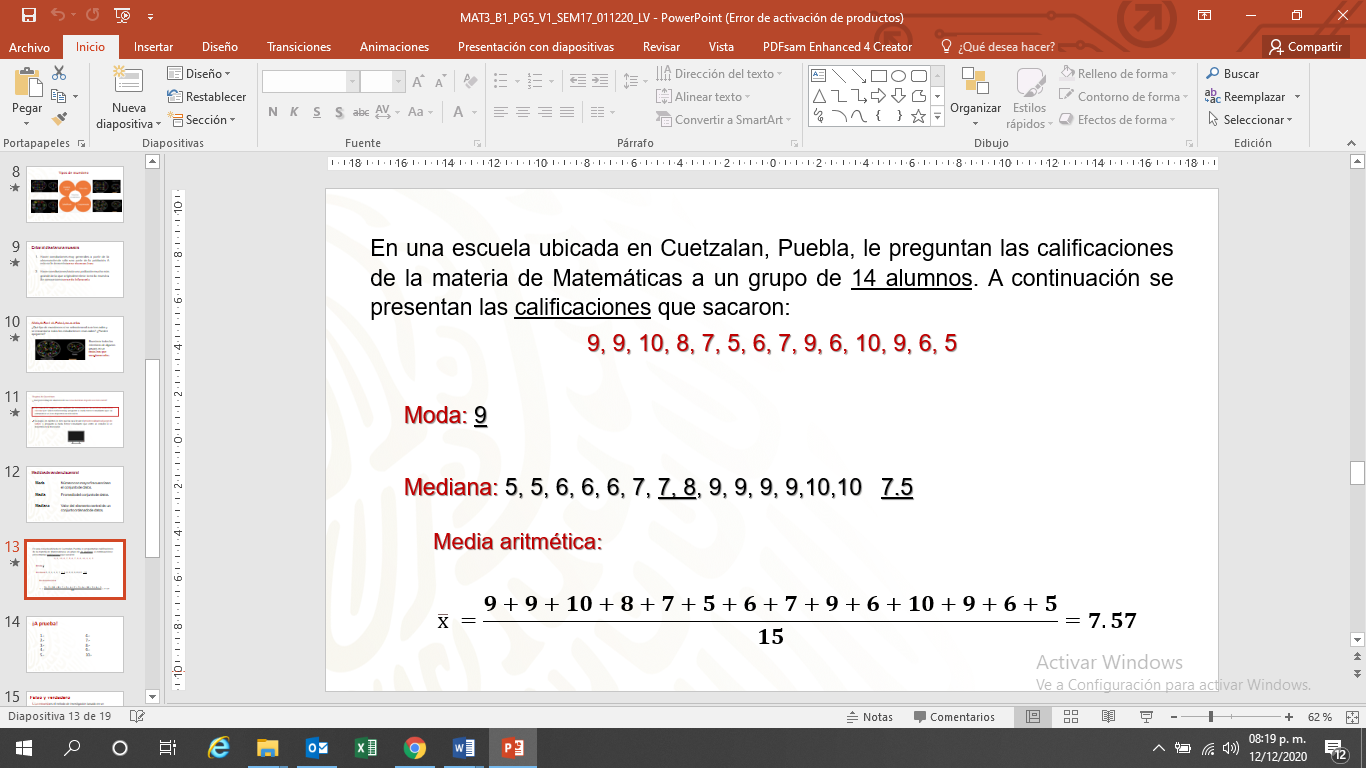
Con estas calificaciones se pide que calcules las medidas de tendencia central. Inicia con la moda; si observas los datos, el valor que más se repite es 9.
La mediana la obtienes ordenando los datos de menor a mayor o viceversa, y buscas el dato central, en este caso, son el 7 y 8 porque el total de datos es par, obtienes la media o promedio, tienes que 7.5 es la mediana.
La media aritmética es el promedio de las calificaciones, es decir, se suman todas las calificaciones y se dividen entre el número de alumnos y el resultado es la media aritmética, comúnmente conocida como promedio. Para este ejemplo la media es 7.57.
Para recapitular, aprendiste que la encuesta se utiliza a fin de obtener, con ahorro de tiempo y esfuerzo, datos de una población. También que, para garantizar resultados fiables, se escoge una muestra adecuada a la información deseada.
El entrevistador debe diseñar una serie de preguntas en un lenguaje claro para que los consultados respondan sin problema.
Una vez identificada la población por estudiar, el tamaño de la muestra debe ajustarse para que la información obtenida represente a aquélla.
Los resultados se pueden representar con tablas o gráficas; también se pueden calcular una o más medidas de tendencia central para mayor análisis de los datos.
Realiza el siguiente ejercicio: Enumera en tu cuaderno del 1 al 10, leerás las 10 preguntas y tú ustedes únicamente escribirás la respuesta.
Las preguntas del 1 al 8 corresponderán a falso y verdadero, y en las preguntas 9 y 10 tendrás que seleccionar el inciso de la respuesta correcta.
En las siguientes proposiciones coloca “F” si el enunciado es falso y “V” si es verdadero.
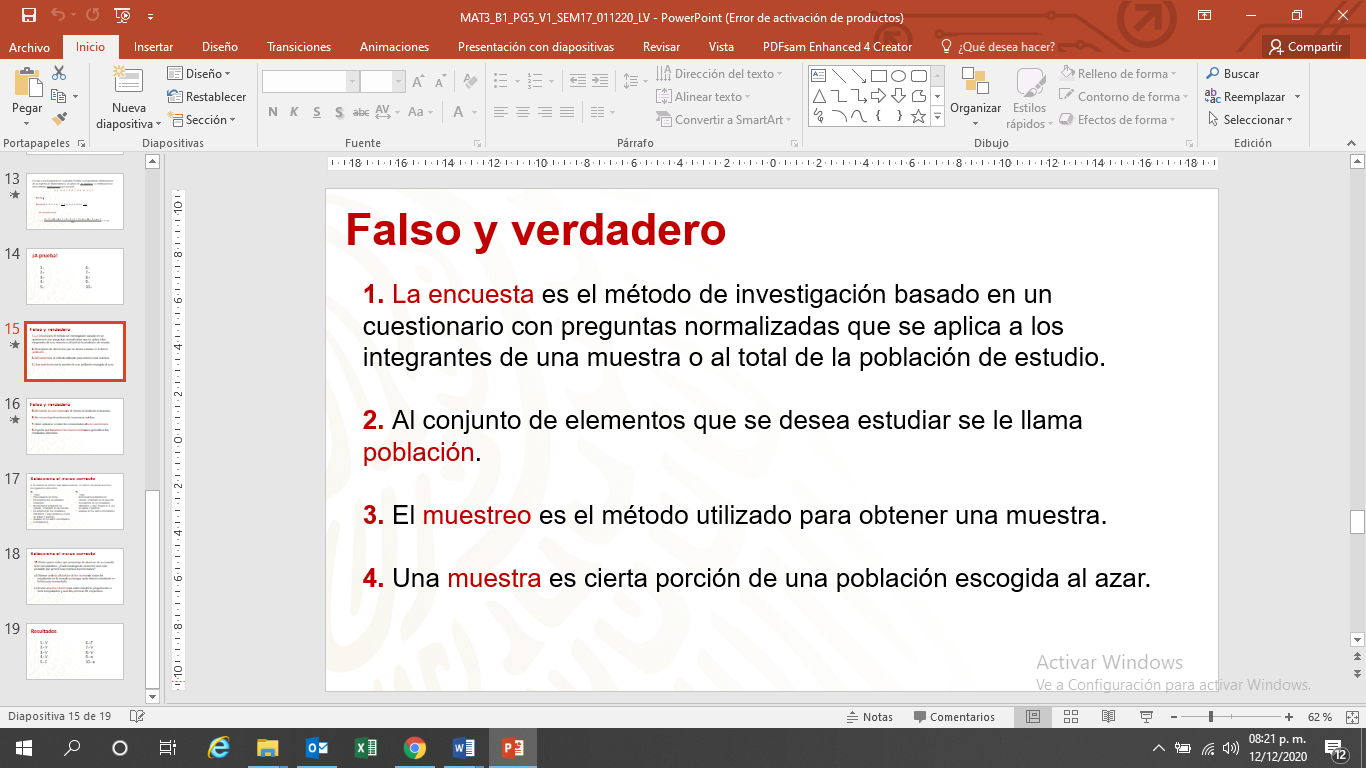
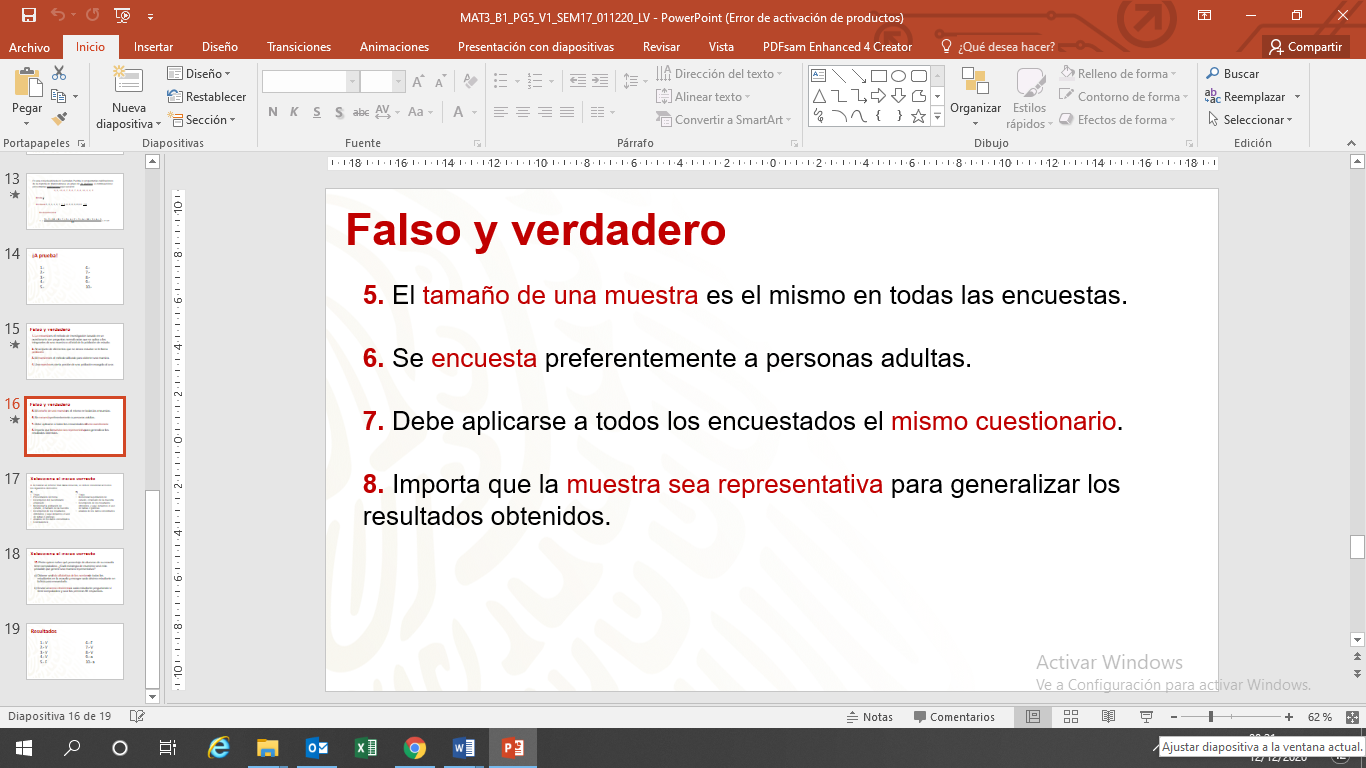
Ahora deberás seleccionar el inciso correcto de las preguntas 9 y 10.
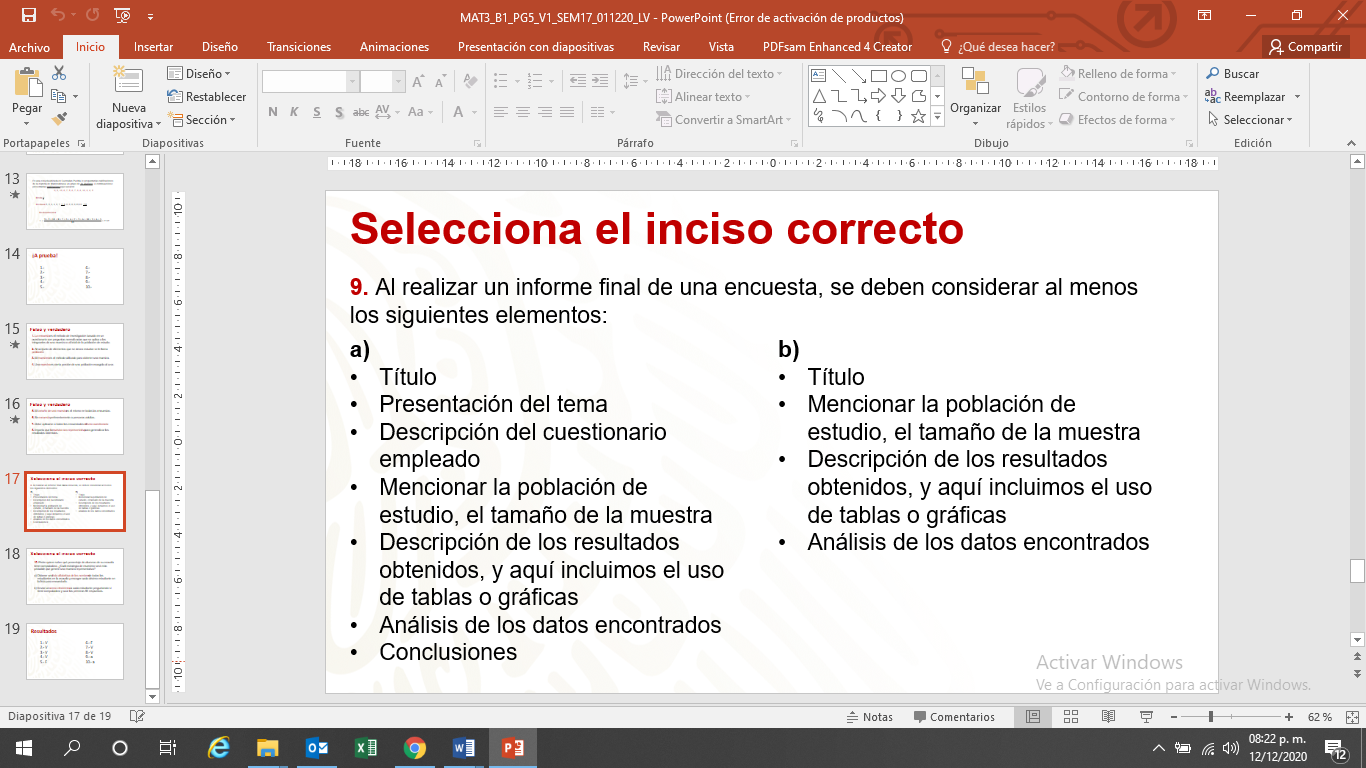
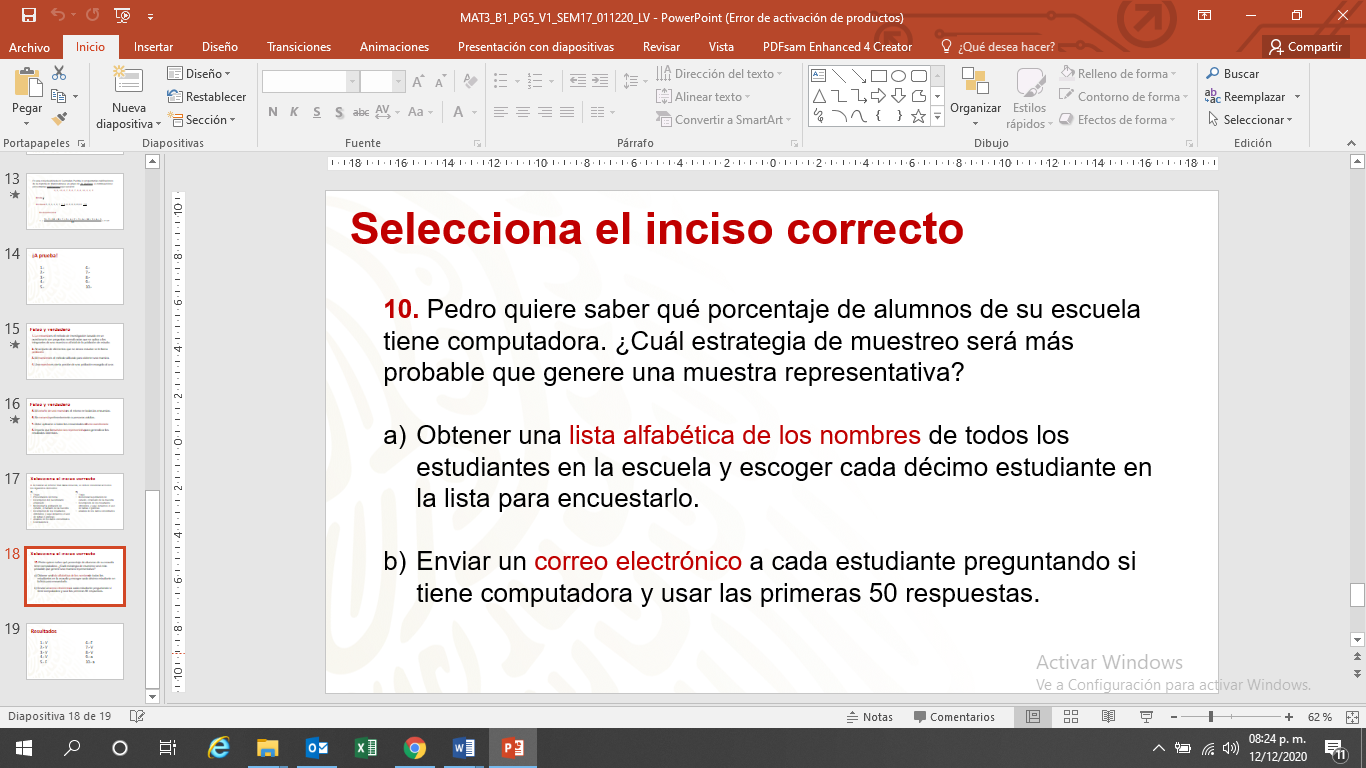
Con estos resultados, espero que les sirvan de base para medir qué tanto se apropiaron del tema visto.
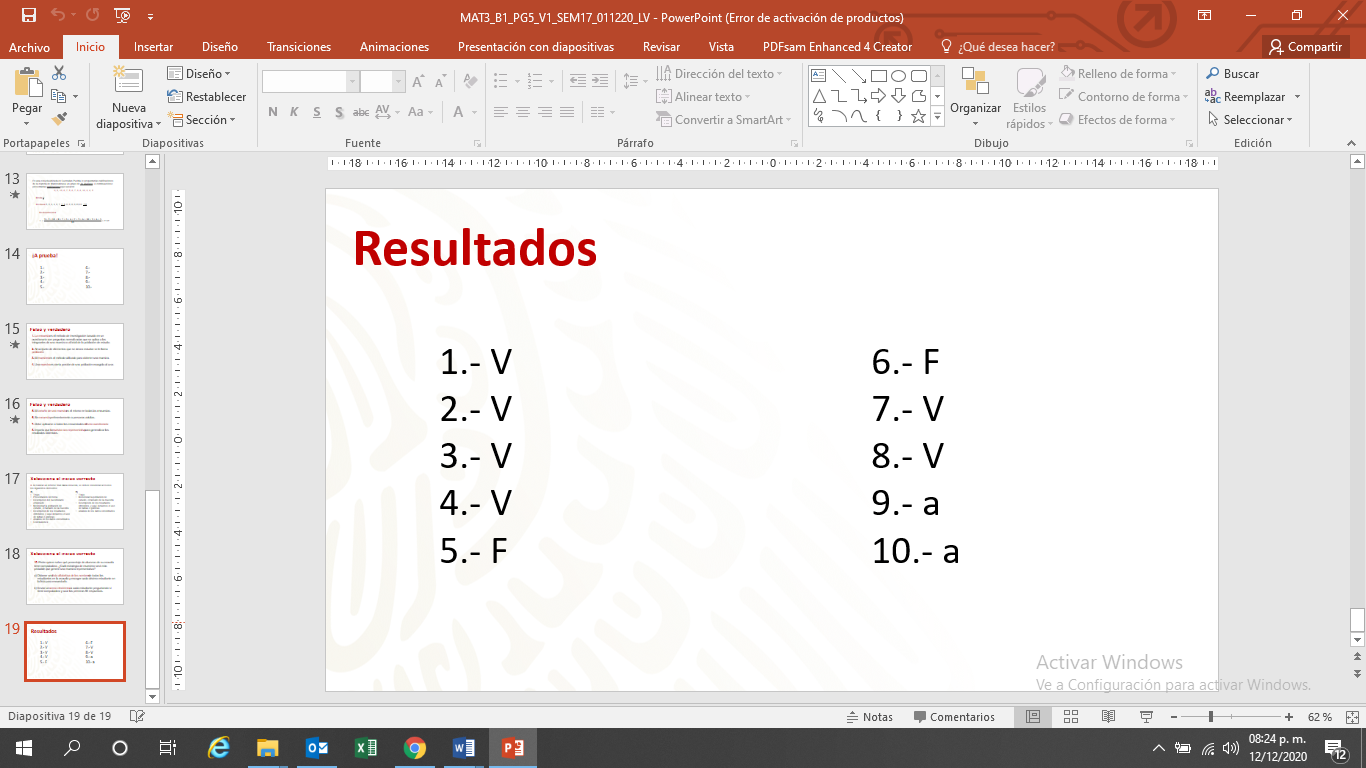
El reto de hoy:
Para resolver dudas o ejercitar lo aprendido, te puedes apoyar en tu libro de texto, en caso de que no cuentes con él, lo puedes encontrar en Internet, en la página de la Comisión Nacional de Libros de Texto Gratuitos.
¡Buen trabajo!
Gracias por tu esfuerzo.
