Sucesiones, propiedades de figuras y sus expresiones algebraicas
Sucesiones, propiedades de figuras y sus expresiones algebraicas
Aprendizaje esperado: verifica algebraicamente la equivalencia de expresiones de primer grado, formuladas a partir de sucesiones.
Énfasis: formular problemas a partir de distintas expresiones algebraicas de primer grado para modelar sucesiones o propiedades de figuras geométricas.
¿Qué vamos a aprender?
En esta sesión, formularás problemas a partir de distintas expresiones algebraicas de primer grado para modelar sucesiones o propiedades de figuras geométricas. Es decir, te convertirás en escritor de problemas matemáticos.
¿Qué hacemos?
Analiza la información para formular un problema a partir de la siguiente sucesión aritmética.
3, 7, 11, 15…
Reflexiona en las siguientes preguntas:
¿Qué observas en la sucesión dada?
¿Cuál es el primer término?
¿Qué identificas entre el término 1 y el término 2?
¿Cuál es el término 5 de la sucesión?
La sucesión del primer término es 3 y del segundo término es 7 La diferencia entre ellos es cuatro, o cada término va aumentando de cuatro en cuatro. De esta manera, 3 + 4 = 7
Por lo tanto, cuatro es la constante aditiva, debido a ello, se cuenta con una progresión aritmética. La sucesión es creciente, es decir, va aumentando.
Ahora, formula un problema o una situación que pueda ser resuelta mediante la sucesión 3, 7, 11, 15…
Recomendaciones para escribir un problema:
- Considera un contexto viable
- Usa oraciones breves.
- Verifica que se tengan todos los datos para que pueda ser resuelto.
Ejemplo de la formulación del problema matemático.
Se usará un contexto de dinero. En este caso, en billetes de 20 pesos.
Problema. Tienda de abarrotes
La tía de Juan Manuel le pidió que le ayudara los fines de semana en su tienda de abarrotes, y le ofreció, como pago inicial, tres billetes de veinte pesos. Pero se dio cuenta que Juan Manuel es muy trabajador, y le dijo que, si continúa con esa disposición, las siguientes semanas, de manera consecutiva, recibiría una cantidad mayor de billetes de veinte pesos, por lo que la segunda semana recibió siete billetes, la tercera recibió once billetes y la cuarta recibió quince billetes de veinte pesos. A partir de la semana veinte le va a mantener el pago constante.
¿Qué expresión algebraica modela esta sucesión?
Para modelar la expresión algebraica, organiza la información como se muestra en la tabla, donde: El número de término (n) representa las semanas, y el valor del término de sucesión (a), la cantidad de billetes.

Ahora justifica que se trata de una progresión aritmética.
Obtén la diferencia del valor de dos términos:

- Siete (valor del segundo término de sucesión) menos tres (valor del primer término de sucesión), igual a cuatro.
- Once (valor del tercer término de sucesión) menos siete (valor del segundo término de sucesión), igual a cuatro.
- Quince (valor del cuarto término de sucesión) menos once (valor del tercer término de sucesión), igual a cuatro.
En todas las restas es igual a cuatro, ¿qué representa este valor?
La diferencia entre los términos de la sucesión es constante, por lo que se tiene una progresión aritmética. Por lo tanto, este valor representa la constante de progresión.
Observa nuevamente la tabla y analiza para modelar la expresión algebraica. Partirás del 4 que representa la diferencia entre términos consecutivos de sucesión, o también llamada constante de progresión. Después, multiplica la constante de progresión por el primer término, “n1”; en este caso, se escribe como subíndice, por lo tanto, queda el término “4n1” Sustituye el valor de “n1” donde obtienes: 4(1) = 4

¿Qué representa este producto?
¿El valor del primer término de la sucesión?
Este producto no representa el valor del primer término de la sucesión porque el primer término de la sucesión vale tres.
Presta mucha atención para no confundirte.
Retoma la explicación, se trata de una progresión aritmética, por lo tanto, se utiliza la regla general donde:

Como puedes observar, la expresión algebraica para el término n1, es:
an = 4(n) – 1
¿Qué representa este valor?
El primer término de la sucesión.
Ahora, comprueba si el procedimiento anterior funciona para los otros términos de la sucesión y después obtener la expresión general.

Para el valor del primer término de sucesión (a1), se tiene:
4(1) – 1 = 3
Para el valor del segundo término de sucesión (a2), se tiene:
4(2) – 1 = 3
Para el valor del tercer término de sucesión (a3), tenemos cuatro por tres, menos uno, igual a once.
4(3) – 1 = 3
Y para el valor del cuarto término de sucesión (a4) tenemos cuatro por cuatro, menos uno, igual a quince.
4(4) – 1 = 3
¿Qué significan estos resultados?
Que corresponden a los valores de la sucesión 3, 7, 11, 15…, por lo que queda comprobado que la expresión algebraica permite conocer los términos de la sucesión.
Por lo tanto, puedes responder a la pregunta:
¿Qué expresión algebraica modela esta sucesión?

Ahora, responde a Juan Manuel:
¿Cuántos billetes le dio su tía en la semana veinte?
¿Cuánto dinero le debe pagar a partir de la semana veinte?
A partir de la expresión algebraica, sustituye “n” por su valor numérico, en este caso, 20:

¿Qué significa setenta y nueve en el contexto del problema?
La cantidad de billetes que recibió Juan Manuel por las veinte semanas trabajadas.
¿Cuánto le pagarán a partir de las veinte semanas?
$1 580.00
Se escribió un problema que dio sentido y significado a la sucesión:
3, 7, 11, 15…
El problema diseñado contenía todos los datos para que pudiera ser contestado.
A continuación, observa cómo Agustín escribió su problema.
Pensó en una sucesión de figuras, todas ellas cuadrados, donde la figura 1 mide por lado 3 cm; la figura 2, mide 7 cm; la figura 3 mide 11 cm, y así sucesivamente.
Y planteó dos preguntas:
¿Cuál es el perímetro de la figura 10?
¿Habrá una figura que mida de 30 cm de lado?
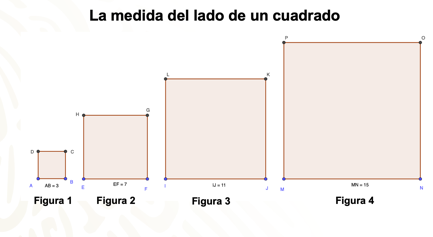
Analiza si con la expresión general que se estableció en el problema de Juan Manuel puedes contestar las preguntas de Agustín.
Por lo tanto, la expresión algebraica que modela el contexto del problema queda definida como:

Ahora responde la pregunta del problema de Agustín:
¿Cuál es el perímetro de la figura 10?
A partir de la expresión algebraica, sustituye “n” por su valor numérico, en este caso, diez:

¿Qué significa treinta y nueve en el contexto del problema?
Como “an” es la medida del lado del cuadrado, entonces 39 es la medida del lado del cuadrado que ocupa la posición 10 en la sucesión de figuras. Si el lado mide treinta y nueve, entonces su perímetro es:
39 (4) = 156 cm.
¿Habrá una figura que mida 30 cm de lado?
Como la expresión algebraica 4n – 1 representa la sucesión de los lados de los cuadrados cuya medida de sus lados es un número impar, entonces:
El treinta no es un número impar, por lo tanto, en la sucesión no habrá una figura cuya medida de su lado sea treinta cm.
A continuación, formula y resuelve a partir de la siguiente sucesión aritmética dada en las figuras.
La figura 1 se ha formado por 3 barras, la figura 2 está formada por 5 barras, la figura 3 por 7 barras, de manera tal que se tiene la sucesión: 3, 5, 7…
Ahora, formula un problema que pueda ser resuelto mediante esta sucesión.
Recuerda que, para ello, debes considerar un contexto viable, usar oraciones breves y verificar que se tengan todos los datos para que pueda ser resuelto.
Observa con atención el siguiente ejemplo de un problema formulado, partir de la sucesión aritmética anterior.
Problema. Soldador, triangulo
Un soldador está fabricando una estructura de acero con barras de ángulo y comienza a partir de tres barras formando un triángulo. En la segunda parte del proceso forma dos triángulos con cinco barras, y en la tercera parte del proceso forma tres triángulos con siete barras, es decir, la estructura está formada, hasta el momento, por tres triángulos.
a) De continuar con el mismo proceso de construcción, ¿cuántas barras tendrá la figura 50?
b) ¿Cuál es una expresión algebraica que sirve para encontrar el número de barras necesarias para formar la figura (n)?
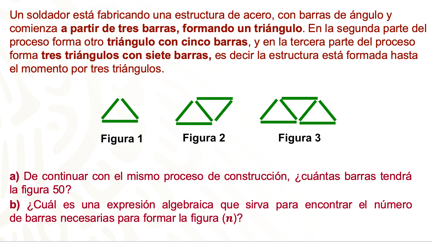
Modela la expresión algebraica que sirva para encontrar el número de barras necesarias para formar la figura (n).
Organiza la información como se muestra en la tabla, donde el término o la figura (n) representa la cantidad de triángulos y su valor (a), la cantidad de barras.

Ahora comprueba que se trata de una progresión aritmética.

- Cinco (valor del segundo término de la sucesión) menos tres (valor del primer término de la sucesión) es igual a dos.
- Siete (valor del tercer término de la sucesión) menos cinco (valor del segundo término de la sucesión) es igual a dos.
¿Cuál es el valor de las diferencias obtenidas?
El resultado de las restas es el mismo.
¿Qué representa este valor?
La diferencia entre dos términos consecutivos de la sucesión y, como es constante, se cuenta con una progresión aritmética, por lo tanto, este valor es la constante de progresión.
Analiza la tabla anterior para encontrar la expresión algebraica de la sucesión. Partirás del dos, que representa la diferencia entre términos consecutivos de la sucesión, después multiplica la constante de progresión por el primer término “n1” por lo tanto, queda el término “2n1” ahora sustituye el valor de “n1” en el término:

Continua con la progresión aritmética, se utiliza la regla general, donde:

Por lo tanto, la expresión general de la sucesión es:
an = 2n +1
Comprueba si el procedimiento anterior funciona para los otros términos de la sucesión.

¿Qué significan estos resultados?
El valor de los términos de sucesión dados, es decir, que la expresión algebraica es correcta, por lo tanto, se puede responder una de las preguntas.
La expresión algebraica modelo para el contexto del problema queda definida como:

Finalmente, responde las preguntas planteadas al principio:
¿Cuántas barras tendrá la figura 50 de la sucesión?
A partir de la expresión general de la sucesión “an”, sustituye los valores:

¿Qué significa este valor?
La cantidad de barras que se necesitan para llegar a la figura cincuenta de la estructura que hace el herrero.
A continuación, profundizarás en sucesiones con figuras.
Resuelve a partir de las sucesiones dadas en las figuras:
Problema. Figuras, círculos.
Se tienen los tres primeros términos de la sucesión de figura de círculos azules y amarillos.
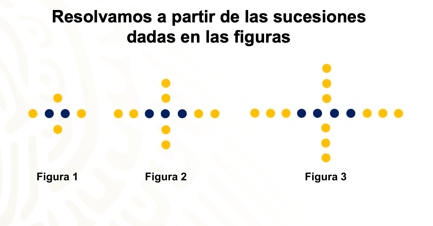
Analiza y resuelve la primera parte de la tabla.

¿Cuántos círculos azules hay en las figuras 1, 2 y 3?
En la figura 1 hay dos, en la figura 2 hay tres y en la figura 3 hay cuatro.
¿Cuántos círculos amarillos hay en las figuras 1, 2 y 3?
En la figura 1 hay cuatro, en la figura 2 hay ocho y en la figura 3 hay doce.
¿Cuántos círculos hay en total en cada figura?
La figura 1 tiene un total de seis círculos. La figura 2 tiene un total de once círculos y la figura 3 tiene un total de dieciséis círculos.
Ahora continua con la siguiente parte.
¿Cuál es la expresión algebraica para calcular cualquier cantidad de círculos azules?, ¿qué se debe hacer para encontrar esa expresión algebraica?
Primero, identificar la diferencia entre términos consecutivos de la sucesión. Observa en la tabla.

¿De cuánto es la diferencia?
Es de uno.
¿Recuerdas cómo plantear la expresión?
Se multiplica la diferencia, que es uno, por el primer término de la sucesión “n”; al operar, se obtiene uno por uno, igual a uno.
Ahora no harás uso del término general, por lo tanto, al término “1n” se le suma uno para igualar a dos y queda la expresión:
1n + 1
Comprueba si el procedimiento anterior funciona para los otros términos de la sucesión.
1 + 1 = 2 sí cumple
2 + 1 = 3 sí cumple
3 + 1 = 4 sí cumple
Ya cuentas con la expresión algebraica para los círculos azules, es:
an = n + 1
¿Cuál es la expresión algebraica para calcular cualquier cantidad de círculos amarillos?, ¿qué debes hacer para encontrar esa expresión algebraica?
De la misma manera, identifica la diferencia entre términos consecutivos de la sucesión. Observa en la tabla.

¿De cuánto es la diferencia?
Es de cuatro.
¿Recuerdas como plantear la expresión?
Se multiplica la diferencia que es cuatro por el primer término de la sucesión “n”; al operar, se tiene: 4(1) = 4
¿Qué representa este producto?
El valor del primer término de la sucesión, ya que es cuatro.
Comprueba si el procedimiento anterior funciona para los otros términos de la sucesión.
4(1) = 4 sí cumple
4(2) = 8 sí cumple
4(3) = 12 sí cumple
Ya cuentas con la expresión algebraica para los círculos amarillos, es:
an = 4n.
¿Cuál es la expresión algebraica que determina los círculos totales de las figuras?
Observa la tabla.

La regla general de la sucesión para cualquier término n:
an = 5n + 1
Para comprobar que la expresión “5n + 1” es correcta, sustituye el valor posicional (número de figura) en la expresión, por lo tanto:
a1 = 5(1) + 1 = 6
a2 = 5(2) + 1 = 11
a3 = 5(3) + 1 = 16
Sí cumple la expresión general de la sucesión, que es: “5n +1”, ya que es igual al total de círculos azules y amarillos por figura.
¿Cuántos círculos en total tendrá la figura 1 000?
A partir de la ecuación modelo 5n + 1, sustituye valores y te queda:
a1000= 5(1000) + 1
= 5000 + 1
= 5001
¿Qué significa este valor?
La cantidad de círculos que tendrá la figura 1 000.
En esta sesión, formulaste problemas a partir de distintas expresiones algebraicas de primer grado para modelar sucesiones aritméticas y encontrar el enésimo número de la sucesión. Además de que se plantearon problemas a partir de una sucesión, como el caso de Juan Manuel y el soldador.
Consulta las actividades de tu libro correspondientes a sucesiones y expresiones algebraicas.
Recuerda que el Programa de Educación a Distancia Aprende en Casa es un material de apoyo, al igual que tu libro de texto, y que puedes consultar otras fuentes para complementar lo aprendido aquí.
El reto de hoy:
Resuelve algunos de los problemas o ejercicios sobre sucesiones aritméticas de tu libro de Matemáticas.
Después, escribe un problema matemático a partir de una sucesión.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas