Teorema de Pitágoras
Teorema de Pitágoras
Aprendizaje esperado: resuelve problemas que implican el uso del teorema de Pitágoras.
Énfasis: enunciar el Teorema de Pitágoras.
¿Qué vamos a aprender?
Enunciarás el teorema de Pitágoras, analizarás su utilidad y uso en tu vida diaria. También identificarás las ecuaciones que se pueden utilizar para encontrar cualquier dato del triángulo rectángulo.
Dichas ecuaciones, las encontrarás realizando despejes en el enunciado del Teorema de Pitágoras.
Los materiales que utilizarás serán: cuaderno de apuntes, juego de geometría, bolígrafo, marcador, colores, lápiz y goma.
Además, necesitarás algunas hojas de colores, triángulos recortables en cartulina y sólo si es posible, una hoja milimétrica.
Recuerda que anteriormente, analizaste las características del triángulo rectángulo, y la asombrosa relación que tiene el área de los cuadrados de cada uno de sus catetos, con el área del cuadrado de la hipotenusa.
¿Qué hacemos?
¿Qué dice el Teorema de Pitágoras?
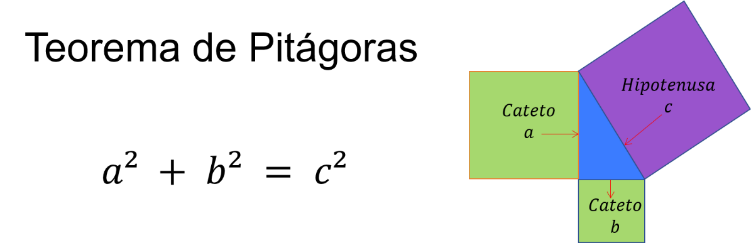
Si se tiene un triángulo rectángulo de lados a, b y c, siendo a y b los catetos, es decir, los lados que forman un ángulo recto, y se construyen cuadrados usando cada uno de los lados del triángulo, con sus áreas respectivas a cuadrada, b cuadrada y c cuadrada
Entonces este teorema dice que “En todo triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa”.
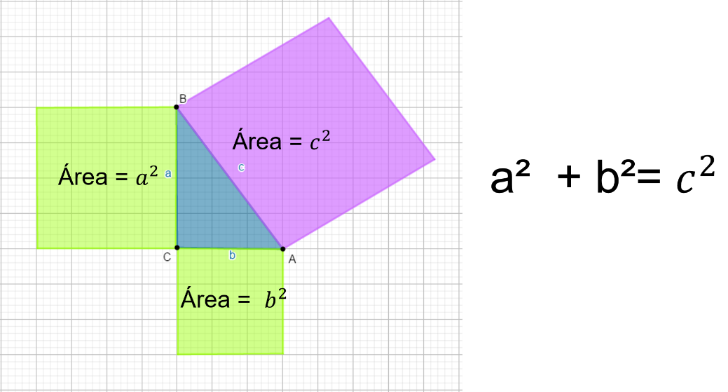
En otras palabras, si a un triángulo rectángulo, le trazas un cuadrado en cada uno de sus lados, siendo este lado, la medida del lado del cuadrado, y obtienes el área de cada uno de ellos; el área del cuadrado de la hipotenusa, que es el lado mayor, es igual a la suma de las áreas de los cuadrados de los catetos, que son los lados menores que forman el ángulo recto.
Algebraicamente se puede decir: a cuadrada + b cuadrada = c cuadrada, en donde c es la hipotenusa, a y b son los catetos.
Tal vez es un poco complejo, ya que es el enunciado de un Teorema que, por cierto, es una herramienta muy útil. Realizarás un ejemplo numérico, para que se despejen las dudas.
Numéricamente podrías decir que, si tienes un triángulo rectángulo con medidas de 3, 4 y 5 unidades por lado, y obtienes sus cuadrados, las áreas serán 9, 16 y 25 unidades cuadradas respectivamente. Al sumar las áreas de los cuadrados de los catetos, tienes 9 +16 es igual a 25 unidades cuadradas, que son las que le corresponden al cuadrado de la hipotenusa.
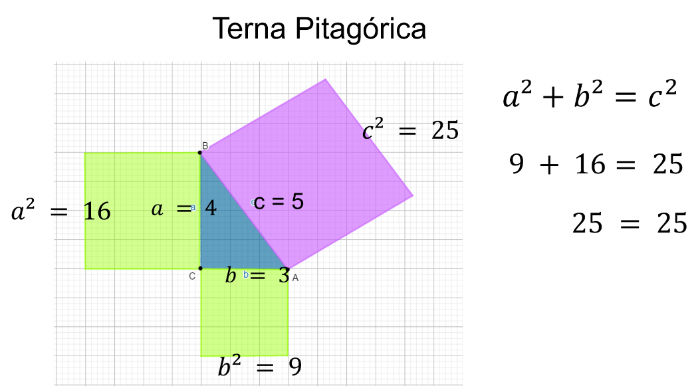
Este ejemplo no sólo es una aplicación del Teorema de Pitágoras, también es lo que se denomina una “terna Pitagórica”, es decir, tres números naturales que cumple con el Teorema de Pitágoras.
Se pueden encontrar otras ternas pitagóricas, desde los babilonios y los egipcios ya se conocía esta relación entre tres números con la característica de que cumplen el teorema de Pitágoras.
Las ternas pitagóricas pueden ser primitivas o no primitivas.
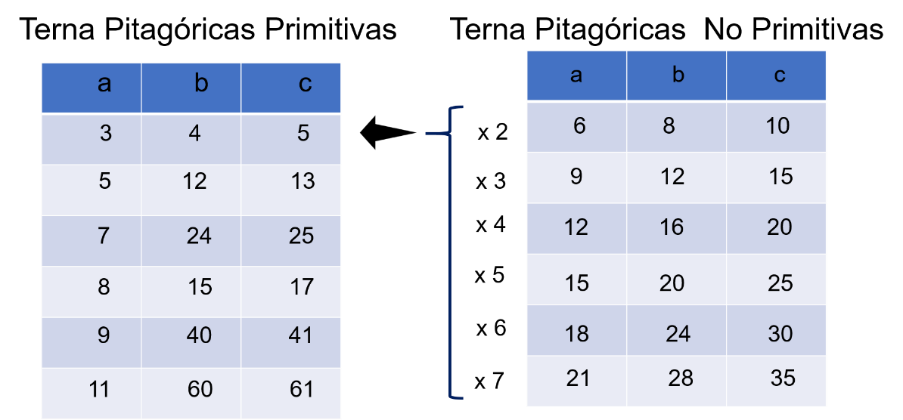
En la primera tabla observas ternas primitivas, en la segunda tabla tomas la primera terna y obtienes múltiplos de ella que, a su vez, son ternas pitagóricas. Así puedes hacer con cada terna pitagórica, y cómo puedes observar, hay infinidad de ternas.
Todas las ternas cumplen el Teorema de Pitágoras. Recuerda tomar apuntes en tu cuaderno para que revises este importante tema las veces que sea necesario.
Analiza, ¿qué pasa si cambia la posición del triángulo o las literales con las que se representa?, ¿cambiará la expresión algebraica?

Considera el caso. Observa los triángulos rectángulos. Expresa algebraicamente el teorema considerando la hipotenusa en función de las otras dos variables.
Recuerda que la hipotenusa es el lado más grande y se encuentra enfrente del ángulo recto. Entonces:
En el primer triángulo tienes que z es la hipotenusa, por lo tanto, x y y son los catetos, entonces obtienes que z cuadrada = x cuadrada + y cuadrada y en el segundo triángulo, observa que la hipotenusa es m y los que forman el ángulo recto son los lados n y o. Considéralos como catetos, obteniendo que m cuadrada = n cuadrada + o cuadrada.
Ya observaste que no importa en qué posición se encuentre el triángulo rectángulo, la hipotenusa siempre se obtiene a través de la suma de los catetos y, las expresiones anteriores son útiles cuando nos falta la hipotenusa, pero no siempre es así. Para calcular algún cateto es necesario utilizar otras expresiones, las cuales obtienes a partir del teorema de Pitágoras. ¿Cómo podrías obtener estas expresiones?
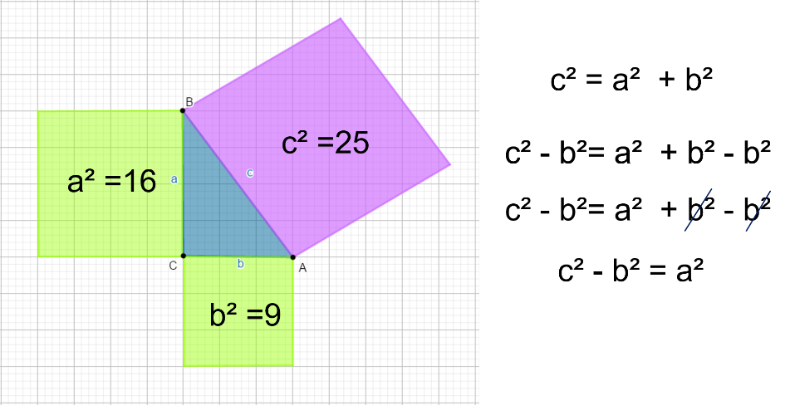
Partes de la expresión general c cuadrada = a cuadrada + b cuadrada, que observaste anteriormente para calcular la hipotenusa, ahora, resta el termino b cuadrada en ambos miembros para que en el segundo miembro se cancele el término b cuadrada por tener signo opuesto y la ecuación queda así, c cuadrada – b cuadrada = a cuadrada.
Ahora, observa la misma situación, pero tomando en cuenta las áreas de cada cuadrado de los lados del triángulo rectángulo y ocupa números. Observa que, si restas el área del cateto b de 9 unidades cuadradas al área de la hipotenusa de 25 unidades cuadradas, obtienes 16 unidades cuadradas, que son las que le corresponden al área del cateto a.
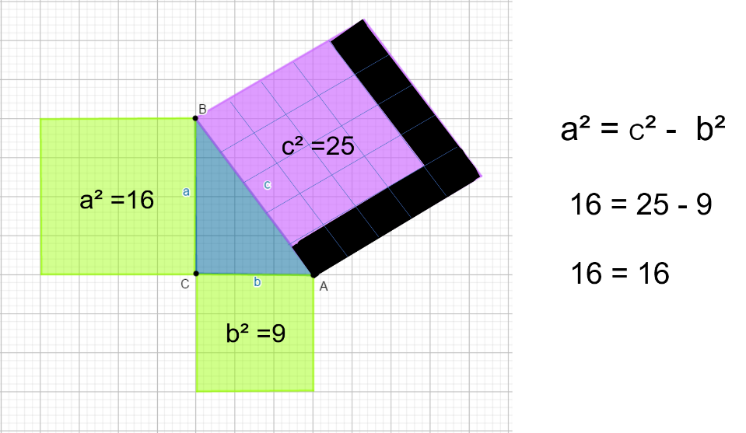
Con lo anterior compruebas a través de las áreas, la relación del cateto faltante con los datos proporcionados. La operación que corresponde es la resta del cuadrado del cateto conocido del cuadrado de la hipotenusa.
¿Qué piensas que ocurra, si el valor desconocido ahora es el cateto b? Observa:
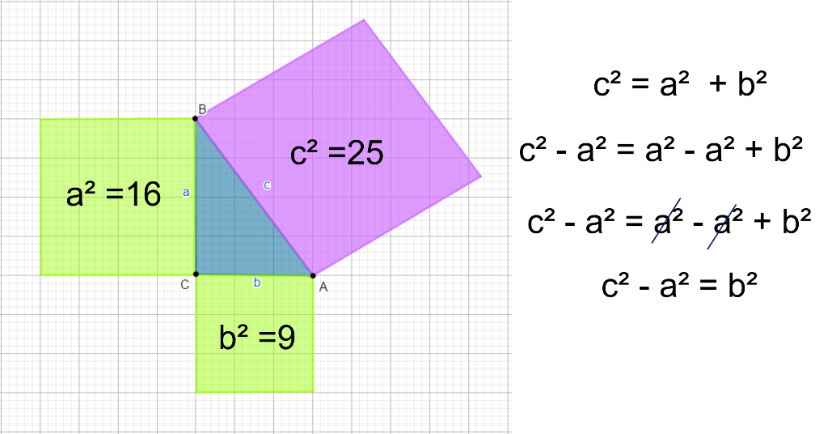
Nuevamente partes de la expresión general c cuadrada = a cuadrada + b cuadrada que utilizas para calcular la hipotenusa. Ahora resta el término a cuadrada en ambos miembros para cancelar a cuadrada que tiene el mismo valor, pero signo opuesto y queda así, c cuadrada – a cuadrada = b cuadrada.
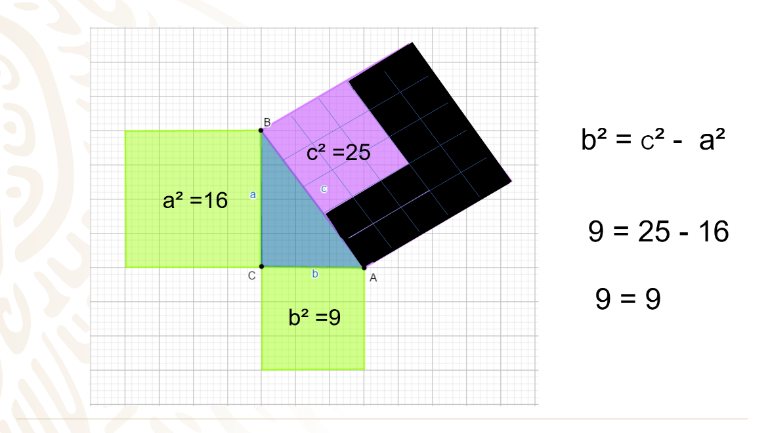
Observa cómo al trabajar con las áreas de cada lado del triángulo rectángulo y, al restar ahora el área del cateto a de 16 unidades cuadradas del área de la hipotenusa de 25 unidades cuadradas, encuentras que el resultado es de 9 unidades cuadradas es el área del cateto b.
¿Qué ocurre si cambias de posición a los triángulos y utilizas otras literales? Analiza estos triángulos rectángulos.
¿Cómo puedes obtener sus expresiones correspondientes?

En el primer triángulo rectángulo, que además es isósceles, es decir, sus lados son iguales, obtienes que el cateto x cuadrada = z cuadrada – y cuadrada y que el cateto y cuadrada = z cuadrada – x cuadrada. En este triángulo el valor de x es igual a y.
En el triángulo naranja tienes que el cateto n cuadrada = m cuadrada – o cuadrada y el cateto o cuadrada = m cuadrada – n cuadrada. Por ser triángulo rectángulo y escaleno, todos sus valores serán diferentes.
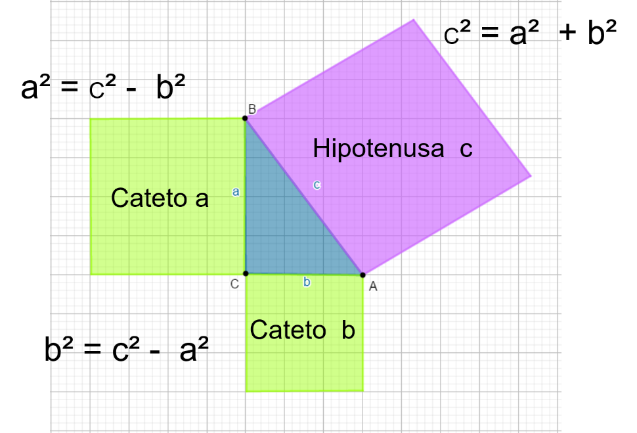
Puedes utilizar una expresión algebraica equivalente dependiendo del dato desconocido o el lado que se quiera calcular: Utilizando el triángulo original a, b, c, tienes que, cuando falta la hipotenusa, usas c cuadrada = a cuadrada + b cuadrada.
Si falta algún cateto puedes utilizar: a cuadrada = c cuadrada – b cuadrada o bien, b cuadrada = c cuadrada – a cuadrada, que son expresiones equivalentes. Las últimas dos expresiones se parecen mucho.
Si observas al cuadrado de la hipotenusa, le restas el cuadrado del cateto que conoces, es decir, si quieres calcular el cateto “a”, le restas el cuadrado del cateto “b”, pero si quieres el cateto “b”, la diferencia se realiza con el cuadrado del cateto “a”.
Estás calculando el lado faltante como área, es decir, al cuadrado. Pero no has terminado de despejar el lado. Para completar esta acción, con los siguientes triángulos rectángulos, observa:
¿Cuáles son sus lados?, es decir, ¿qué lado es la hipotenusa y cuáles son los catetos?
¿Cuál es la expresión algebraica que le corresponde a cada uno?
¿Cómo cambia cada expresión quitándole el cuadrado?
Los tres lados que componen tu triángulo rectángulo son muy sencillos de ubicar, con las consideraciones antes mencionadas, tienes que h es la hipotenusa, g e i son los catetos.
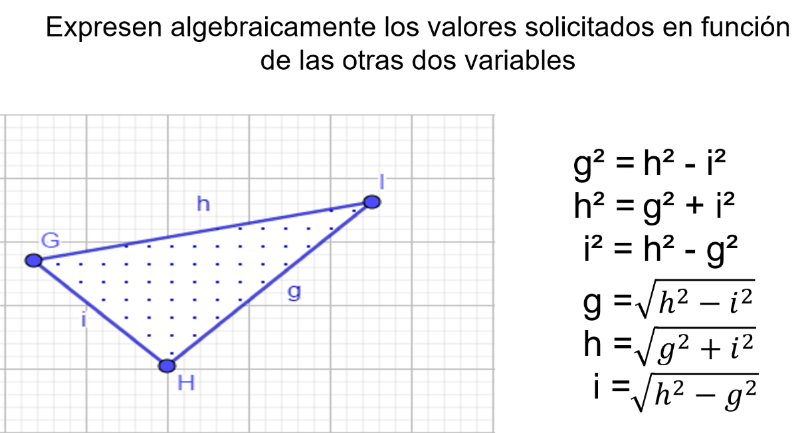
Para el lado g cuadrada=h cuadrada – i cuadrada, para h cuadrada=g cuadrada + i cuadrada y para i cuadrada=h cuadrada – g cuadrada. Ahora termina de despejar.
¿Sabes qué debes hacer para dejar a la literal sin el cuadrado?, debes aplicar la operación inversa del cuadrado, ¿cuál es?, la raíz cuadrada. En el primer miembro, se eliminan las operaciones inversas y obtienes que: g = raíz cuadrada de h cuadrada menos i cuadrada; h = raíz cuadrada de g cuadrada más i cuadrada; e i = raíz cuadrada de h cuadrada menos g cuadrada.
Analiza el siguiente triángulo rectángulo:
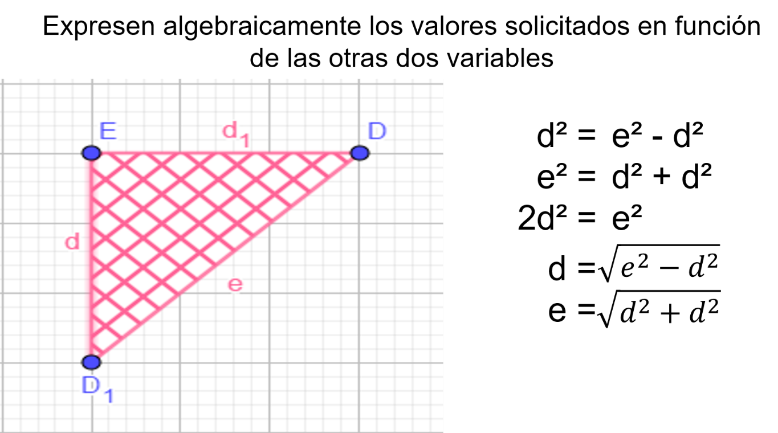
Este triángulo, si lo observas con cuidado, se trata de un triángulo rectángulo e isósceles, en el cual la hipotenusa es e y los catetos son d. Por lo tanto, d cuadrada=e cuadrada – d cuadrada, e cuadrada = d cuadrada + d cuadrada y 2d cuadrada =e cuadrada. ¿Por qué crees que solicitan 2d cuadrada?, porque se pueden agrupar los dos catetos ya que tienen el mismo valor, es decir, se trata de la misma literal.
Ahora, para despejar la literal, tienes que, al aplicar la operación inversa del cuadrado en ambos términos, obtienes que d = raíz cuadrada de e cuadrada menos d cuadrada; y e = raíz cuadrada de d cuadrada más d cuadrada.
Recuerda que para cancelar el cuadrado del primer miembro hay que aplicar en ambos lados la raíz cuadrada. Así que, sumas para el cálculo de la hipotenusa y restas para obtener los catetos.
También recuerda que el orden de la diferencia es importante, al cuadrado de la hipotenusa se le debe restar el cuadrado del cateto.
Analiza los siguientes triángulos rectángulos:
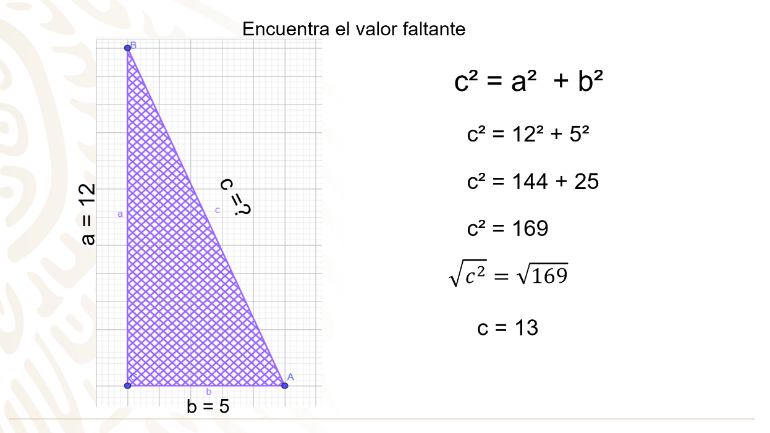
Inicia con un triángulo rectángulo en donde conoces la base de 5 unidades (cateto), su altura de 12 unidades (el otro cateto). ¿Cuánto mide su hipotenusa?
Parte de la expresión general para calcular la hipotenusa c cuadrada = a cuadrada + b cuadrada, sustituyes los valores conocidos de a y b y empiezas a realizar las operaciones: 12 al cuadrado es 144 y 5 al cuadrado es 25, al sumar las cantidades obtienes 169. Para encontrar el valor de la hipotenusa, aplicas la operación inversa del cuadrado que es la raíz cuadrada en ambos miembros. Eliminando ambas en el primer miembro por ser operaciones contrarias y obtienes la raíz cuadrada del segundo miembro, obtienes que el valor de la hipotenusa es de 13 unidades.
¿Reconociste los valores obtenidos? Se trata de una terna pitagórica. ¿Recuerdas por qué se le nombra así? Porque todos los valores son naturales y cumplen el Teorema de Pitágoras.
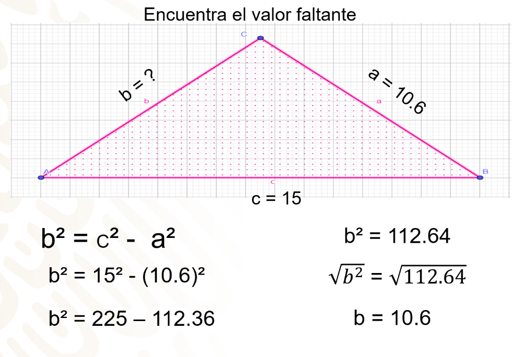
La posición cambió en este triángulo y el valor desconocido ahora es un cateto, ya que el valor más grande es el de la hipotenusa de 15 unidades y el del otro cateto de 10.6 unidades.
La fórmula con la que iniciarás es b cuadrada = c cuadrada – a cuadrada para calcular el cateto. Sustituyes los valores conocidos de la hipotenusa y el otro cateto.
El cuadrado de 15 es 225 y el de 10.6 es 112.36, al realizar la diferencia obtienes 112.6, para encontrar el valor del cateto, aplicas la operación inversa del cuadrado, que es la raíz cuadrada en ambos miembros, en el primer miembro se cancelan las operaciones inversas y la raíz cuadrada en el segundo miembro es de 10.6 unidades.
Truncando el resultado a décimas, puedes observar que el resultado tiene el mismo valor que el otro cateto, esto se debe a que se trata de un triángulo rectángulo isósceles.
Conocerás la manera práctica a través de un problema, observando el siguiente video del minuto 5:42 a 8:53 que te dará un ejemplo:
- Aplicaciones del teorema de Pitágoras
https://www.youtube.com/watch?v=bjkf7a-VUhA
Debes leer y comprender qué es lo que solicitan en el problema. Si analizas el procedimiento que siguieron para resolver el problema anterior, puedes concluir que es importante:
- Contar con un esquema o dibujo en donde puedas ubicar los datos proporcionados en el problema. Siempre tendrá la forma de un triángulo rectángulo para poder aplicar el Teorema de Pitágoras.
- Identificar el valor faltante para aplicar la fórmula que le corresponda.
- Sustituir los datos en la ecuación y realizar operaciones
Resuelve los siguientes problemas:
Inicia con un problema planteado en un libro de texto de Matemáticas de tercero:
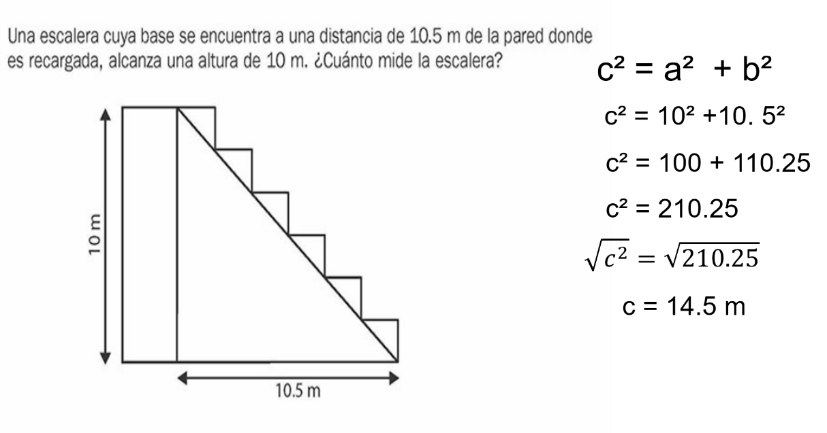
Ubica los datos en el dibujo, la base de la escalera es uno de los catetos de 10.5 m, la altura que alcanza la escalera es el otro cateto de 10 m, por lo tanto, el valor faltante es la hipotenusa.
Ya que identificaste la hipotenusa como valor faltante, entonces partes de la expresión c cuadrada = a cuadrada + b cuadrada, sustituyes los valores conocidos y realizas operaciones, 10 al cuadrado es 100 más 10. 5 al cuadrado es 110.25, al sumarlos obtienes 210.25 y por último calculas su raíz cuadrada, considerando sólo su valor positivo ya que no hay distancias negativas, teniendo 14.5 m, como largo de la escalera.
¿Qué te parece si ahora ayudas a resolver un problema que envió una escuela que quiere colocar unos espejos para su salón de danza?

Los espejos los puedes ingresar en forma diagonal por la puerta rectangular, formando así un triángulo rectángulo y permitir así aumentar el tamaño de los espejos que pueden ingresar. ¿Cómo se puede resolver?
Recuerda los pasos para resolver este tipo de problemas:
Realiza un esquema de la situación. Ubica los datos en el esquema, la altura de la puerta es un cateto de 2m, la base de la puerta es el otro cateto de 1m, por lo tanto, el valor faltante es la hipotenusa.
Sustituye los valores conocidos en la expresión c cuadrada = a cuadrada + b cuadrada, y realiza operaciones: 2 al cuadrado es 4 más 1 al cuadrado es 1, al sumarlos obtienes 5 y por último calculas la raíz cuadrada considerando sólo su valor positivo ya que no hay distancias negativas, obtienes 2.23 m, como diagonal de la puerta.
Con esta medida en la diagonal, puedes afirmar que pueden ingresar espejos de 2 m y 2.2 m. Ahora la escuela solicita ayuda para resolver la siguiente situación.

El salón 1 tiene una puerta de 2m de alto y 2m de ancho, el salón 2 tiene una puerta de 2m de alto y 2.5 m de ancho. ¿Cómo resolver el problema?
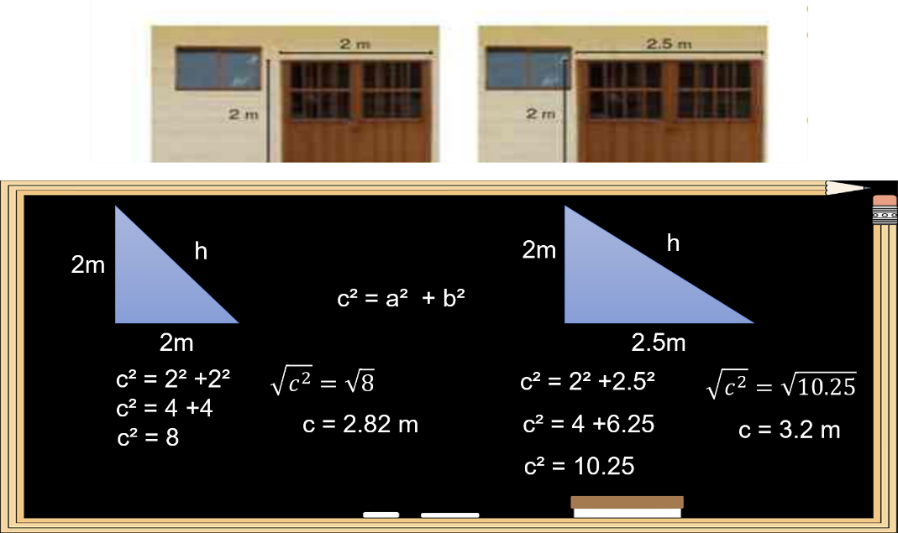
Encuentra la medida de la diagonal de cada una de las puertas, así formas triángulos rectángulos y acomoda los datos que te proporcionan de alturas y bases que serán tus catetos, e inicia con la expresión c cuadrada = a cuadrada + b cuadrada, ya que es la hipotenusa el lado desconocido. Después, sustituyes tus datos en la expresión.
En el salón 1 calcula, 2 al cuadrado es 4 más 2 al cuadrado es 4, al sumarlos obtienes 8 y por último calculas su raíz cuadrada considerando sólo su valor positivo ya que no hay distancias negativas, obtienes 2.82 m como diagonal de la puerta. Para el salón 2, procederás igual, sustituyes: 2 al cuadrado es 4 más 2.5 al cuadrado es 6.25, al sumarlos obtienes 10.25 y, por último, calculas su raíz cuadrada siendo de 3.2 m. el valor de la diagonal.
Con estos resultados puedes afirmar que el salón 2, es el adecuado para ese tipo de espejos. Ya que su diagonal de 3.2 m es mayor a la altura del espejo de 2.5 m.
Ahora, resolverás un problema en el que interviene la semejanza de triángulos y el Teorema de Pitágoras.
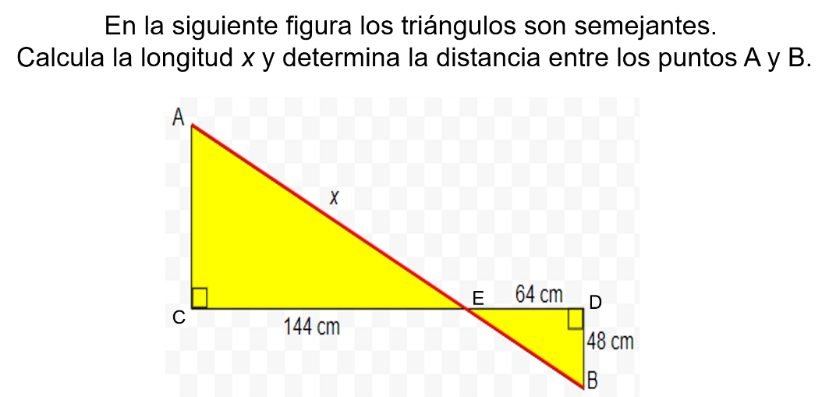
En este problema, para calcular el valor de “x” primero necesitas calcular la altura del triángulo mayor. Y así, poder aplicar el Teorema de Pitágoras en los dos triángulos, ya que, en ambos, falta la hipotenusa y al sumarlas, determinarás la distancia entre los puntos A y B.
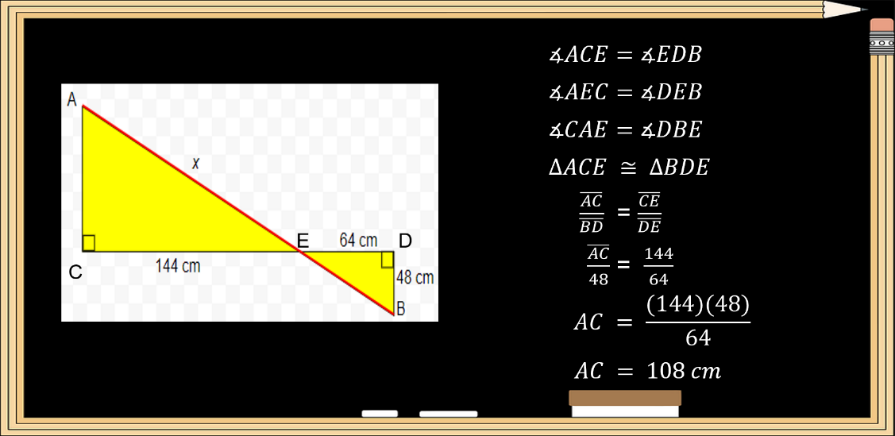
Si observas los dos triángulos puedes afirmar que son semejantes ya que sus ángulos son iguales, es decir, el <ACE=<EDB, el <AEC= <DEB, ya que, al ser opuestos por el vértice, tienen el mismo valor, por lo tanto, el <CAE= <DBE. Al tener el mismo valor los tres ángulos de los dos triángulos, puedes decir que: el triángulo ACE es congruente con el triángulo BDE y así poder plantear que el segmento AC entre el segmento BD es igual al segmento CE entre el segmento DE, sustituyes valores, tienes que el segmento AC entre 48 es igual a 144 entre 64, despejando el lado AC se tiene que es igual a 144 por 48 entre 64, realizando operaciones, obtienes que el lado AC = 108 cm.
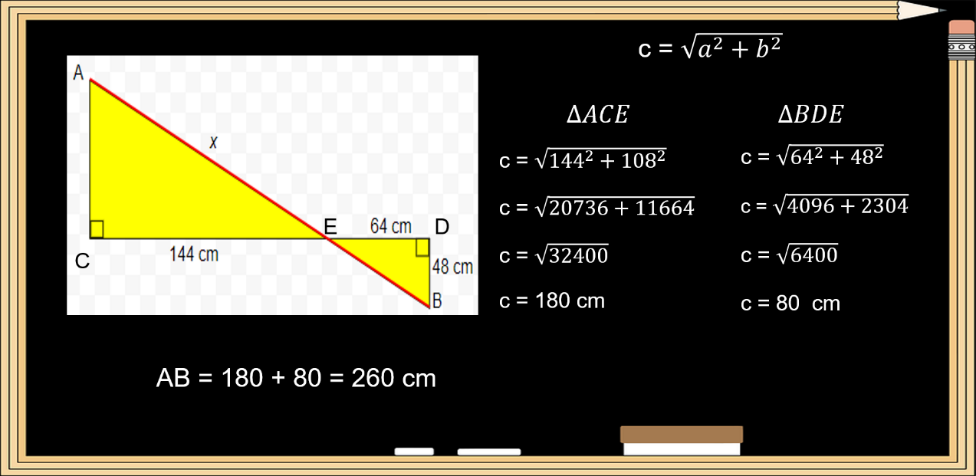
Con ese dato ya puedes calcular el valor de las hipotenusas de ambos triángulos rectángulos.
Partes de la expresión algebraica para calcular la hipotenusa que es c = raíz cuadrada de a cuadrada más b cuadrada; y empiezas a sustituir los valores conocidos de cada triángulo.
En el triángulo ACE sustituyes 144 al cuadrado + 108 al cuadrado, realizando operaciones, obtienes 20,736 + 11,664 = 32400, calculas la raíz cuadrada, tomas el valor positivo y obtienes 180 cm como medida de “x”.
En el triángulo BDE, sustituyes 64 al cuadrado + 48 al cuadrado, realizando operaciones obtienes 4,096 + 2,304 = 6400, calculas la raíz cuadrada tomas el valor positivo obtienes 80 cm como medida del lado BE.
Por último, para calcular la medida del segmento AB que es la suma de las dos hipotenusas tienes que el segmento AB = 180 + 80 = 260 cm.
Realiza el siguiente problema:
Un barco observa en su radar el siguiente modelo, en donde se ubica un faro atrás de él y en las profundidades, una ballena. Con las medidas proporcionadas de forma indirecta.
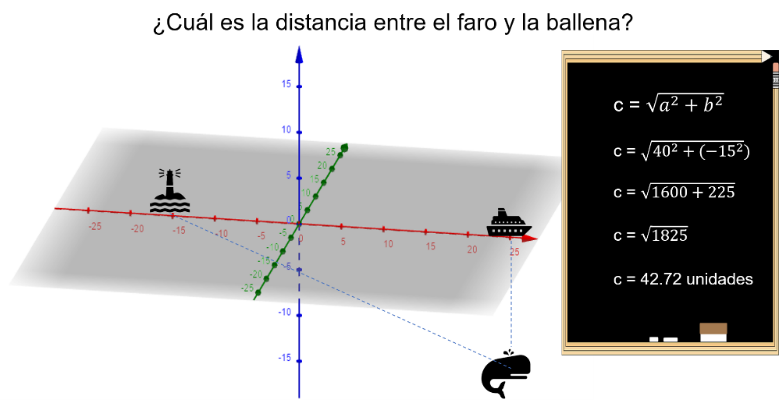
Si observas en el modelo, ahora los valores se proporcionan de forma indirecta, ya que la base del triángulo no mide 25 unidades, porque el faro se encuentra 15 unidades más hacía atrás.
Entonces ¿Cuánto mide el total de la base? El total de la base es de 25 +15 unidades es decir 40 unidades y el otro cateto, que es la profundidad, de -15 unidades. Al pedir la hipotenusa utilizas la expresión c = la raíz cuadrada de a cuadrada + b cuadrada, sustituyes valores y obtienes c = la raíz cuadrada de 40 al cuadrado más -15 al cuadrado, realizas operaciones c = a la raíz cuadrada de 1600 más 225, que es igual a la raíz cuadrada de 1825, calculas la raíz tomando el valor positivo y obtienes que la distancia entre el faro y la ballena es de 42.72 unidades
Tiene una gran aplicación el Teorema de Pitágoras y una gran variedad de problemas que tratarás a lo largo de otras sesiones.
El Teorema de Pitágoras tiene una gran influencia social, cultural y educativa. Varios artistas han plasmado, usando diversas técnicas, este resultado geométrico. Incluso otra hermosa representación del teorema es a través del “Árbol de Pitágoras” en donde se genera un fractal.
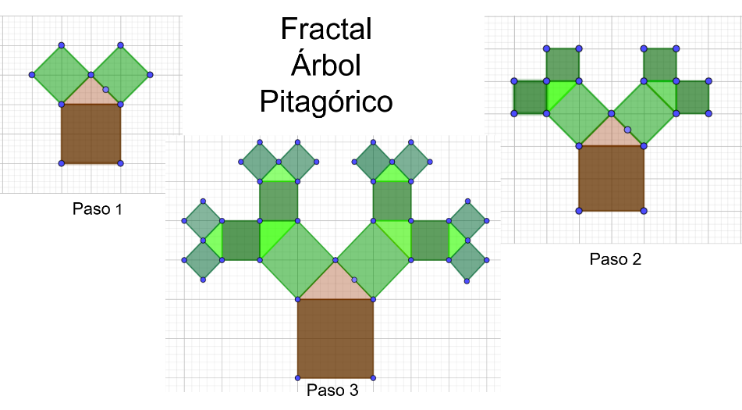
El reto de hoy:
Te sugerimos crear tu propio Árbol de Pitágoras.
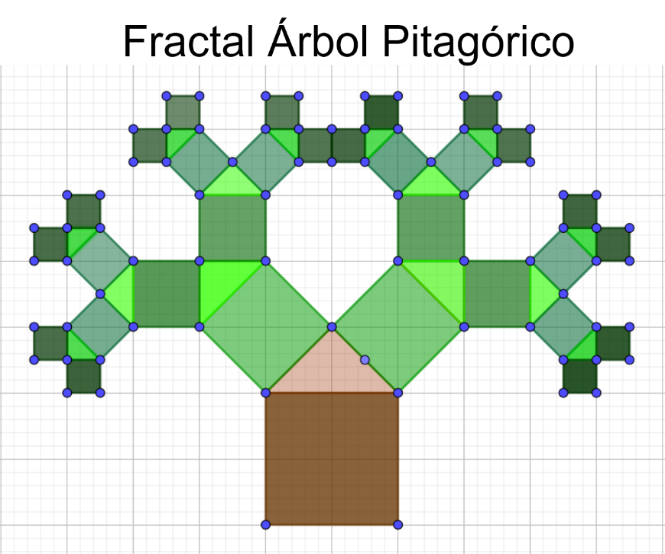
En una hoja milimétrica de preferencia, en el centro de la hoja traza el modelo geométrico del teorema de Pitágoras, la base será la hipotenusa de un triángulo rectángulo isósceles con sus respectivas áreas por lado.
Ahora, cada cateto será la hipotenusa de los siguientes triángulos rectángulos. Si observas tus nuevos modelos, ahora son más pequeños.
Nuevamente, de cada lado de los catetos, realiza la representación geométrica del teorema siendo el lado del cateto la hipotenusa del nuevo, obteniendo modelos más pequeños.
El procedimiento antes mencionado, se repite hasta formar el “Árbol Pitagórico” con las dimensiones y colores que tu creatividad decida.
Te sugerimos buscar en tu libro de texto todo lo relacionado con este tema, y resuelve los ejercicios que ahí se proponen. Para que así puedas enriquecer tu conocimiento.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
