En busca del entero
En busca del entero
Aprendizaje esperado: representación de fracciones de magnitudes continuas (longitudes, superficies de figuras). Identificación de la unidad, dada una fracción de la misma.
Énfasis: establecer la relación entre una fracción (unitaria o no unitaria) que se representa gráficamente y la unidad de referencia al dibujar esta última.
¿Qué vamos a aprender?
Aprenderás a establecer la relación entre una fracción (unitaria o no unitaria), que se representa gráficamente, y la unidad de referencia al dibujar esta última.
¿Qué hacemos?
Inicialmente debes pensar cuántos triángulos tendría la figura completa. ¿Cómo lo sabremos?
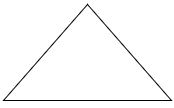
| Si este triángulo representa 1/4 de la figura, entonces en 1/2 de la figura habrá dos triángulos, y …. El reto es dibujar la figura completa |
Si a un entero lo componen dos medios, entonces la figura completa debe tener cuatro triángulos y, ¡cómo podríamos trazar ese entero? No hay una forma única.
Puedes dibujarla utilizando una regla y quedaría así.

Esa es una respuesta acertada. Aunque como bien se comentó la posición en que se colocan los triángulos puede ser diferente.
Observa una respuesta que llegó de Raúl, un alumno de cuarto, él nos explica que, si el triángulo representa 1/4 y quiere tener la figura completa –es decir, la unidad-, entonces le faltan 3/4. Es decir 3 triángulos más, para tener un total de 4 triángulos. Él los dibujó uniéndolos de la siguiente manera.
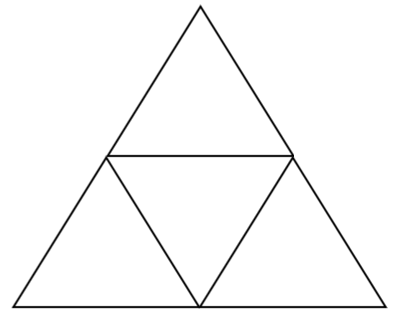
Como puedes observar, esta es otra forma de representar la unidad, considerando la fracción unitaria que nos fue proporcionada.
Y también es correcta.
Otras formas de definir nuestra unidad serían estas, incluida la que nos envió nuestro compañero Raúl.
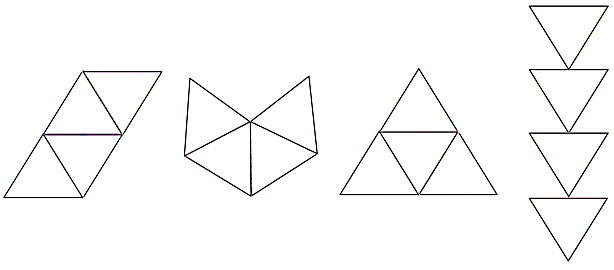
Ahora realizarás otros ejercicios para seguir aprendiendo sobre el tema.
- El siguiente cuadrado representa 2/8 del entero, ¿Cómo será ese entero?

Si el cuadrado representa 2/8 o lo que es lo mismo 1/4, a la unidad le faltarían 6/8 o 3/4, por lo que tendría que dibujar otros tres cuadrados.
La unidad quedaría compuesta por un total de 4 cuadrados y se podría trazar así.
Muy fácil, son dos cuadrados, porque 4/8 equivalen a 2/4 y, a su vez, equivalen a 1/2 por lo que la mitad de cuatro cuadrados son dos cuadrados, que se destacan en color morado.
¿Y si solo se te pide que dibujes 6/8 de la figura?
Pues dibujarías solo tres cuadrados, porque 6/8 es equivalente a 3/4
Vas comprendiendo cómo relacionar una fracción con su representación gráfica en la unidad a la que pertenece. - El siguiente es un trapecio y representa 2/6 de una figura. ¿Cómo será la unidad de la que esta figura forma parte?
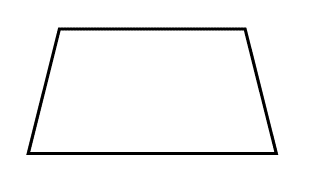
El trapecio representa 2/6 que equivalen a 1/3. ¿Cierto?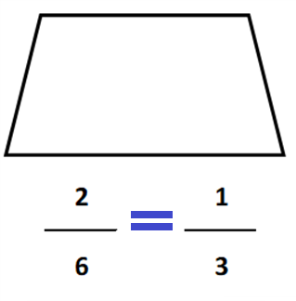
Es correcto. Si un entero está formado por 3/3 o 6/6 entonces para completar la unidad faltan 2/3 o 4/6
¿Cuántos trapecios tendrías que dibujar entonces para completar la figura?
Tendrías que dibujar otros 2 trapecios.
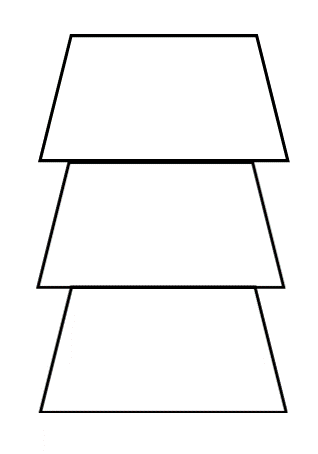

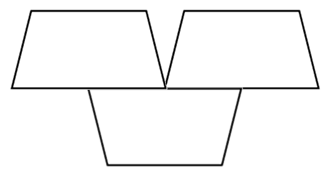
- En este ejercicio, la unidad está formada por un total de tres trapecios, y que puede verse de varias maneras. Como las que tenemos en pantalla.

Fíjate en el siguiente pentágono, representa 1/2 de una figura. ¿Cómo representarías 3/2?
Si el pentágono representa 1/2, y queremos tener una figura que represente 3/2, que es más que una unidad, entonces te faltan 2/2 que equivalen a una unidad.
Entonces, tendrías que dibujar otros 2 pentágonos para representar 2/2, por lo 3/2 pueden dibujarse así.
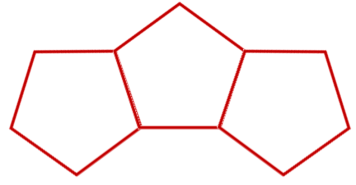
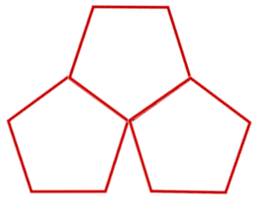
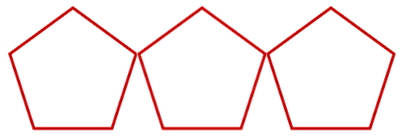
Y otra vez, todas las opciones son correctas.
No hay que olvidar que cualquiera de las representaciones deberá tener tres pentágonos. - Deja las figuras y fíjate en la imagen:

Esta imagen muestra un collar que tiene 3/8 del total de perlas que debe tener. ¿Cuántas perlas se muestran en la imagen? Tres perlas.
¿Cuántas perlas indica el numerador? Tres.
¿Cuántas partes indica el denominador? Indica ocho partes en las cuales está dividido el entero o unidad. Entonces. ¿Cuántas perlas debe tener en total el collar?
Si consideras que tres perlas representan 3/8 del total, entonces 1/8 queda representado por una perla y si el total del collar es 8/8, entonces el collar debe tener 8 perlas.
- En la siguiente imagen se muestra 1/4 del total de palomas que tengo en casa.

Observa que 1/4 de las palomas es igual a cuatro palomas. Entonces dos cuartos de las palomas es igual a:
2/4 es igual a 8 palomas, es decir el doble de las que integran un cuarto de las palomas.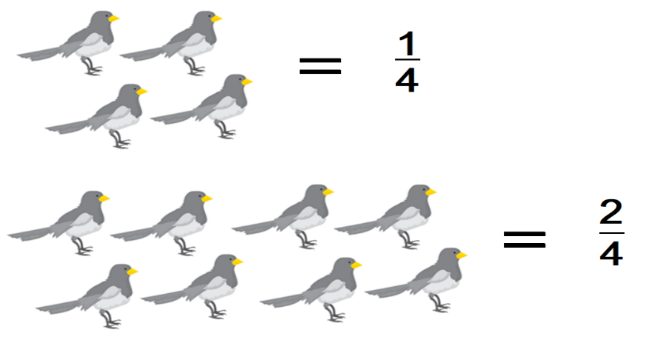
Recuerda que realizaste la suma de:¼ + ¼ + ¼ + ¼ = 4/4
Esto es igual al total del número de palomas que forman la parvada, entonces. ¿Cuántas palomas son el total?

Si en dos cuartos hay 8 palomas, y como sabes 2/4 es igual a 1/2, entonces sumamos otras 8 palomas que representan el otro medio para obtener el total de palomas de la parvada, es decir de la unidad, que son 16 palomas en total. - Tienes ahora un problema más para seguir aprendiendo.
Ángel debe pintar una pared, hasta el momento ha pintado 48 m2, que representan 2/3 partes del total.
¿Cuántos metros cuadrados tiene la barda completa?Considerando que los 48 metros cuadrados que ha pintado Ángel equivalen a 2/3 del total de la barda, divides 48 entre el numerador de la fracción que es 2, para saber cuántos metros cuadrados pintan en 1/3.

Entonces tienes que, aquí, 1/3, son 24 metros cuadrados.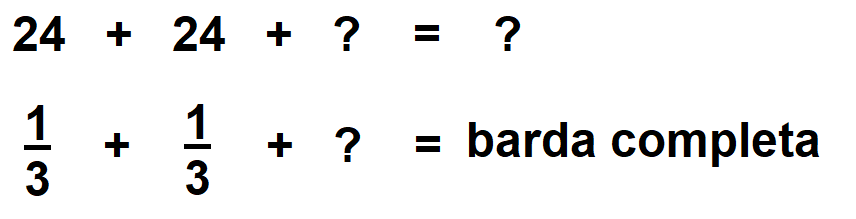
Para concluir basta recordar que un entero está formado por 3/3. Si lleva pintado 2/3, le faltaría por pintar 1/3, por lo tanto, estos serían los metros cuadrados equivalentes que pinta en 1/3, es decir 24 por lo que…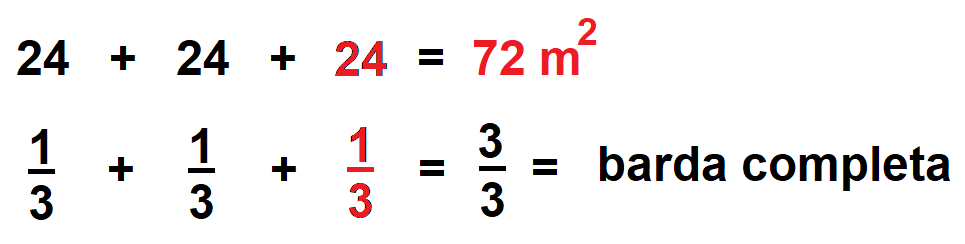
Es una barda muy grande. - En un cine, durante tres funciones se vendieron distintas cantidades de boletos.
¿Cuál es la cantidad de boletos que se vendieron en cada función y cuántos se vendieron en total? 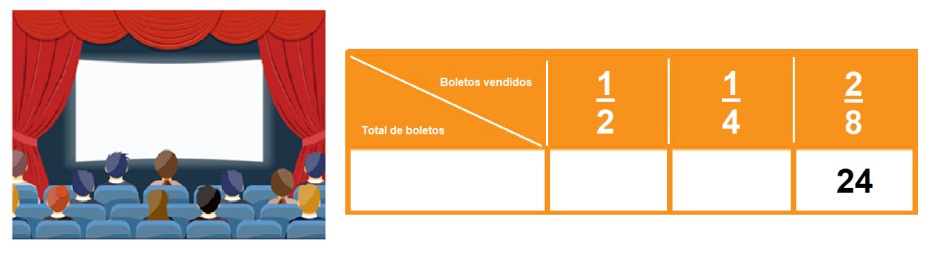
En la cuarta columna se anotó que se vendieron 24 boletos, que representan 2/8 del boletaje.
Entonces, para saber cuántos boletos equivalen a 1/8 dividimos el 24 entre el numerador 2 y da resultado 12, es decir que 12 boletos equivalen a 1/8 del total de boletos.
Y ahora para saber el total de boletos multiplicaríamos los 12 por 8, porque recordemos que 8/8 equivale al total de boletos vendidos, lo que da un resultado 96, que es el total de boletos que debe ir en la primera columna.
Ahora como ya sabes cuántos boletos son en total, puedes calcular 1/2 de los boletos vendidos, ¿Cuántos serían?, es la mitad de los 96 boletos, que son 48.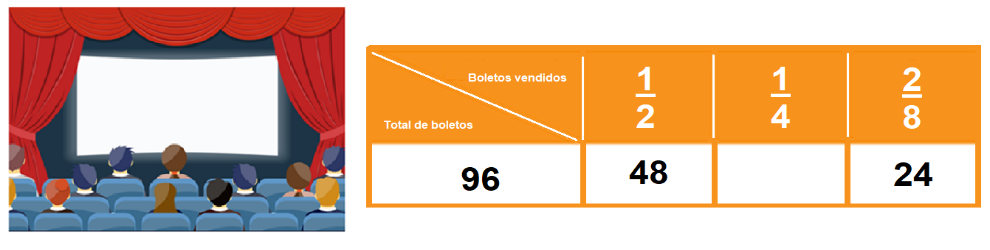
La siguiente columna te indica 1/4. ¿Qué haces ahora?, en esta ocasión solo tienes que recordar que 2/8 es equivalente a 1/4, por lo que 24 boletos es 1/4 del boletaje.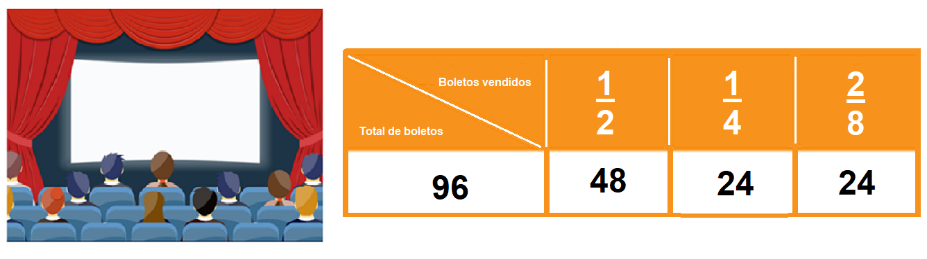
Otra forma en que podrías calcular 1/4 del boletaje es dividiendo 96 entre 4 y obtienes 24 como resultado.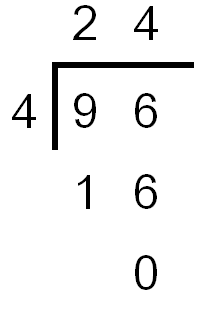
- Vas a trazar una recta de 10 cm.
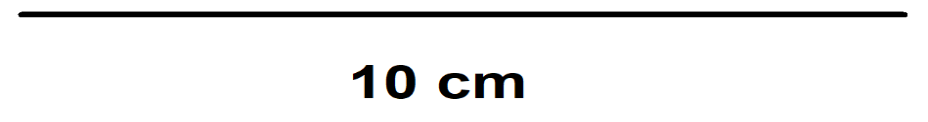
Si esa recta es 1/10 de un entero, entonces, ¿qué longitud tendrá el entero?, ¿Cómo la podemos obtener?
Si el segmento de 10 cm representa 1/10 de la unidad, el denominador me indica que el entero tiene 10 partes iguales. Por lo tanto, para formar una unidad, necesito 10 segmentos iguales que iré trazando delante del que ya tracé para que se prolongue hasta llegar a la longitud indicada.
Entonces, para calcular su longitud en centímetros basta con multiplicar x 10 ya que son 10 segmentos de 10 cm cada uno, por lo que 10 x 10= 100.
Eso quiere decir que la recta trazada tiene una longitud de 100 centímetros. - Observa otro ejemplo similar.
| El siguiente segmento representa 1/6 de la unidad. ¿Cómo es la unidad? |
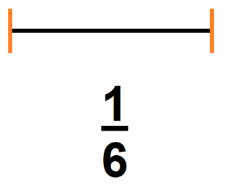
Si el segmento representa 1/6 de la unidad, el denominador me indica que el entero tiene 6 partes iguales.
Por lo tanto, para formar una unidad, necesito iterar (repetir, pues) 6 segmentos iguales, mismos que debo trazar consecutivamente.
Algo importante es que la medida de cada segmento debe ser igual, quedando así.
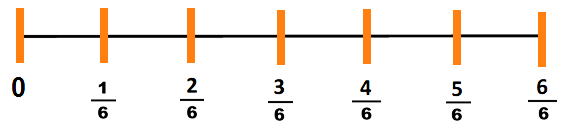
Con este ejercicio ha concluido la sesión de hoy, no sin antes enfatizar lo que aprendiste.
Aprendiste a establecer la relación entre una fracción (unitaria o no unitaria) que se representa gráficamente, y la unidad de referencia al dibujar esta última.
Recuerda que un entero se puede representar con una fracción que tenga el mismo número en el numerador y el denominador. Por ejemplo:
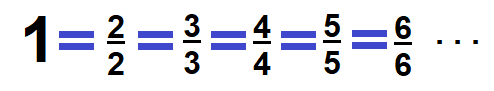
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/