Representación de fenómenos económicos
Representación de fenómenos económicos
Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: representar diferentes situaciones y fenómenos de la Economía.
¿Qué vamos a aprender?
Representarás diferentes situaciones y fenómenos de la economía.
Necesitarás tu cuaderno, lápiz y goma.
Anota las dudas, inquietudes o dificultades que surjan al resolver los planteamientos dados en esta sesión.
Resolverás algunos problemas que impliquen plantear y calcular relaciones mediante ejemplos de ventas de artículos, de costos y otros aspectos similares.
¿Qué hacemos?
Iniciarás estableciendo algunas relaciones.
- Cuando alguien vende artículos, el ingreso que se obtiene se establece por la relación del número de artículos, por el precio unitario de los mismos.
Esto lo puedes expresar como:
Ingreso es igual al número de artículos por el precio del artículo. - Que la ganancia de la venta de un artículo está determinada por la diferencia entre el precio de venta del artículo y el costo de producción.
Esto lo puedes expresar como:
Ganancia es igual a: precio de venta menos costo de producción. - Que el costo fijo está constituido por aquellos gastos que se tienen que afrontar de manera constante en un periodo de tiempo, como, por ejemplo, el pago de alquiler y el pago de servicios, entre otros.
Establecido lo anterior, inicia:
SITUACIÓN 1.
Jorge le compró el automóvil a un amigo. El automóvil es usado y le costó 15,000 pesos. Al contarle a su papá, éste le dice que debió considerar la depreciación que tendrá el vehículo, lo que dejó pensando a Jorge.
Jorge se puso a averiguar y descubrió que el auto se deprecia linealmente en 750 pesos al año, y tiene un valor de desperdicio de 2,250 pesos.
Jorge piensa en ello y se pregunta cómo puede averiguar el valor del auto después de varios años de uso.
Ayuda a Jorge.
Plantea algunas preguntas:
¿Cuál será el valor V del vehículo después de t años de uso? ¿cuál será el valor V después de 6 años? y ¿por cuánto tiempo estará el vehículo en uso?
En este problema vas a realizar diversas consideraciones.
Al decir que se deprecia linealmente, se está considerando que su precio disminuye de manera constante en relación con los años de uso.
El valor de desperdicio hace referencia al valor que tendrá cuando la vida útil del artículo en cuestión finalice.
En el problema se tiene que el Valor del artículo está en función del tiempo de uso.
Inicia por observar cómo se da la depreciación del vehículo. Auxíliate de una tabla de valores para encontrar la función.
- Video 1
https://youtu.be/4cOu1z1JoJI
La función del valor en relación del tiempo se da por la expresión:
Valor en función del tiempo = 15 000-750(tiempo), en donde t es el tiempo transcurrido en años.
Ahora contesta la segunda pregunta:
¿Cuál será el valor V después de 6 años?
Para responder esta pregunta utiliza la expresión anterior y, en ella, sustituye el valor del tiempo por 6, que es el tiempo que tienes como dato.
Ahora contesta la pregunta: ¿por cuánto tiempo estará el vehículo en uso?
En este caso, debes sustituir 2,250 en el lugar de V(t) de la expresión anterior, ya que es el valor comercial del auto al transcurrir el tiempo (t) que estás buscando.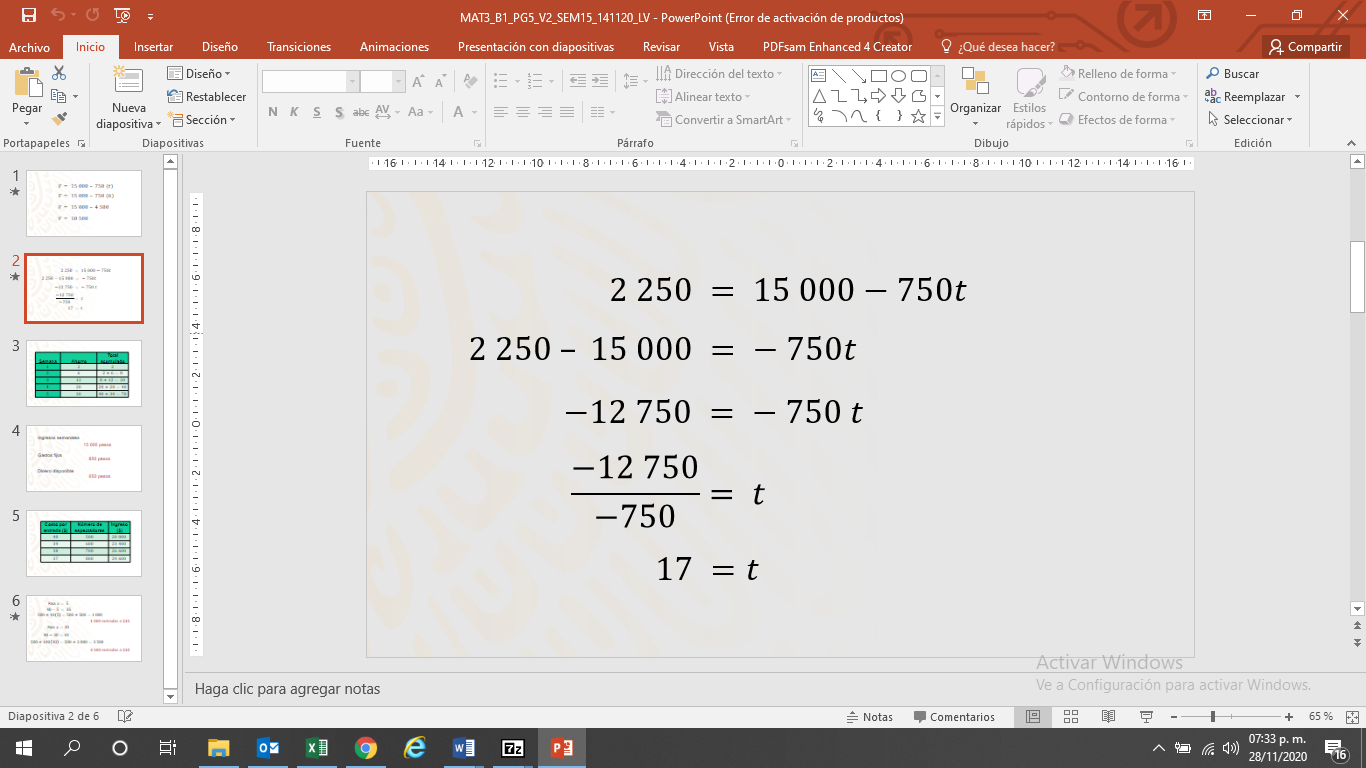
Ahora sabes que el tiempo de uso máximo es 17 años.
Para verificar todo lo calculado, observa la gráfica de la función usada en este problema. - Video 2
https://youtu.be/iG1M2AR0lXE
SITUACIÓN 2.
Alejandra quiere comprarse una caminadora; para ello, cuenta con lo que gana semanalmente al trabajar medio tiempo, que son 1,500 pesos.
El precio de la caminadora es de 5,850 pesos.
Ella ha intentado varias veces ahorrar esa cantidad, y no lo ha logrado porque no toma en cuenta sus gastos fijos.
En esta ocasión se ha decido a ahorrar de manera constante y llevará un control.
Un amigo le ha recomendado que lo haga del siguiente modo.
Observa la tabla: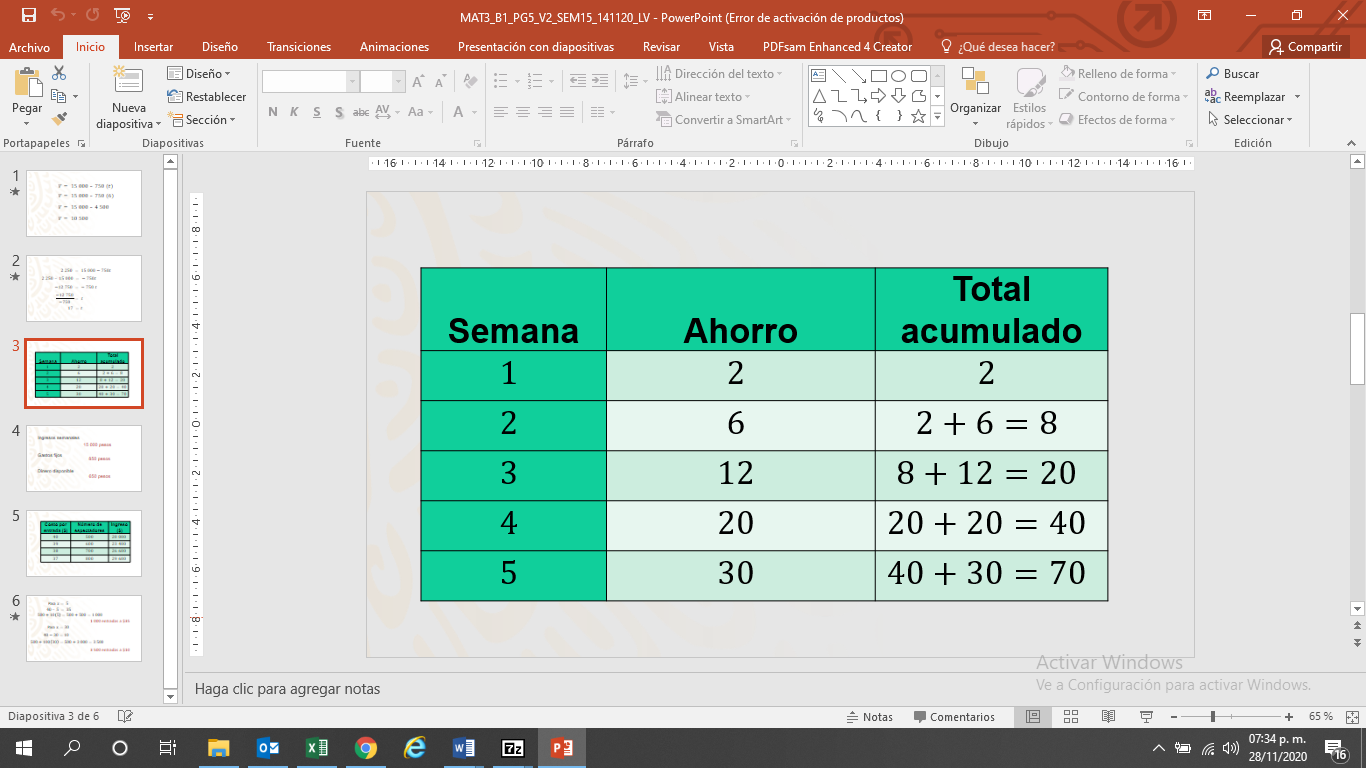
En la tabla puedes ver que se trata de una forma diferente de ahorrar, ya que no se trata de una cantidad fija semanalmente, sino que se inicia con una cantidad pequeña, que en este caso es de 2 pesos, y se incrementará en dos pesos por semana, en comparación con lo aportado la semana anterior, por lo que en la segunda ahorrará 4 pesos adicionales, en la tercera 6 pesos adicionales y así cada ocasión.
Este tipo de ahorro se considera apropiado, pues se incrementa poco a poco lo que vas ahorrando, y así no es difícil. Verifica el comportamiento de ese ahorro: - Video 3
https://youtu.be/E23GGUf7kew
Ella está convencida que lo va a lograr, sin embargo, aún debe hacer cálculos, ya que está preocupada por saber en cuántas semanas logrará reunir los 5,850 pesos del precio de la caminadora.
Ayuda a Alejandra a averiguarlo:
Considera que ella recibe semanalmente 1,500 pesos, tiene gastos fijos semanales de 850 pesos, por lo que el dinero para ahorrar puede ser, máximo de 650 pesos.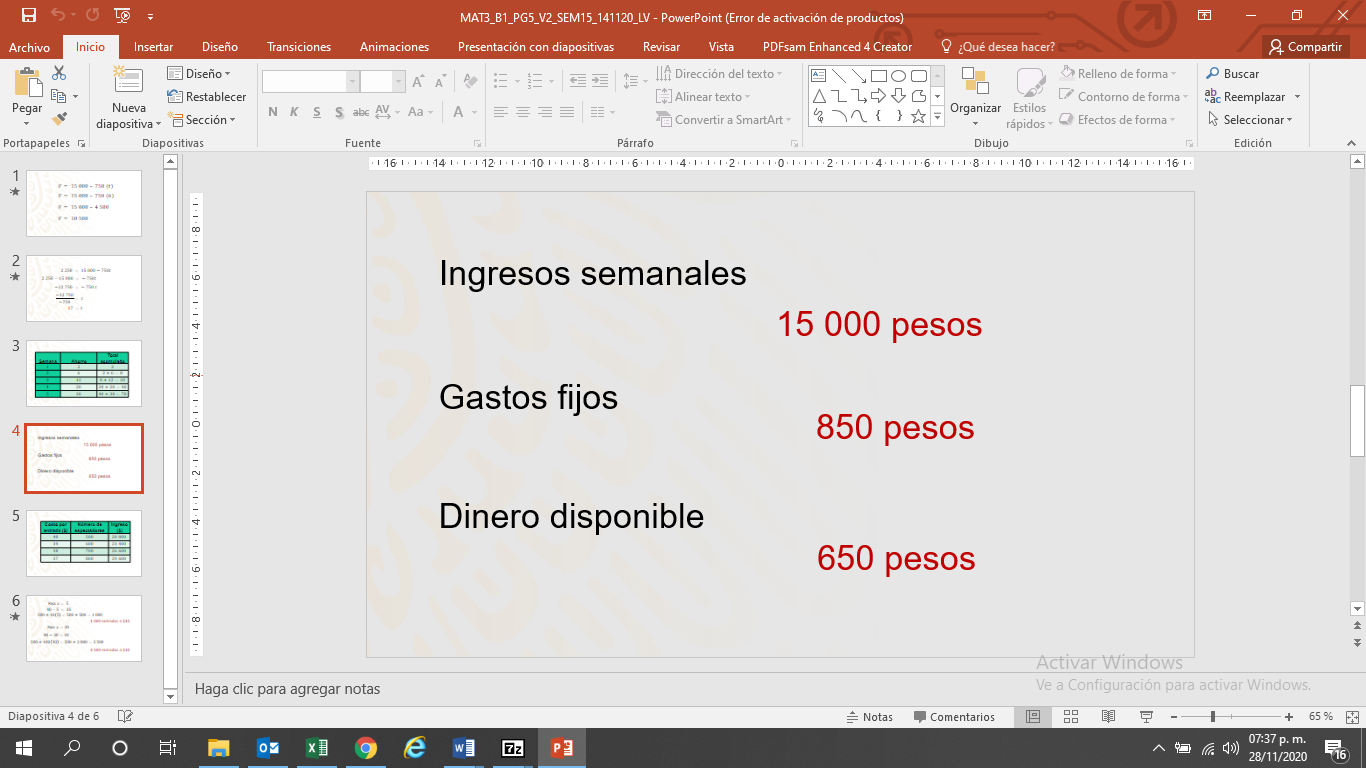
Ayuda buscando la expresión matemática que permita expresar el ahorro que lleva considerando: el número de la semana y la cantidad que le corresponde.
Si nombras “n” al número de la semana y “a” al ahorro correspondiente tienes: - Video 4
https://youtu.be/sClorGWczYA
De este modo, conociendo la expresión matemática que representa al ahorro, Alejandra decide utilizar una hoja de cálculo para conocer el número de semanas que le tomará llegar a su máximo de ahorro posible por semana, que es de 650 pesos, así como calcular el ahorro acumulado en ese momento.
Observa lo que realizó: - Video 5
https://youtu.be/AMGjbX2QZr8
Ahora solo le queda a Alejandra ahorrar como la tabla sugiere, y conseguir la caminadora.
SITUACIÓN 3.
El tesorero del club de teatro escolar estima que, si cobra 40 pesos por entrada, podría tener 500 espectadores. Piensa también que por cada peso que reduzca al costo del boleto, podrían ingresar hasta 100 personas más.
Esto desea explicárselo al director del club de teatro de la escuela para elegir lo que más conviene decidir.
Para ello, elabora la siguiente tabla: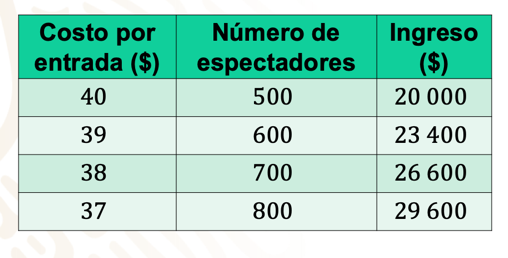
¿Qué es lo que se observa en ella?
Se ve el aumento de los ingresos al disminuir el costo de la entrada un peso, debido al aumento de la asistencia.
Esto es de esperarse debido a que, si es más barata la entrada, más alumnos podrán pagar el costo para ver la obra.
El director entendió que las ganancias mejorarían, así que desea obtener, en una función, 35,000 pesos. Para ello, le deja al tesorero la tarea de calcular el precio de la entrada, y bajo este esquema, lograr esa recaudación. Ayuda al tesorero.
Elabora primero una tabla que permita encontrar cómo va aumentando el número de espectadores al disminuir el costo de la entrada. - Video 6
https://youtu.be/8a0PlDxtXOc
A partir de lo anterior, toma en cuenta que:
Ingresos = costo de la entrada por número de espectadores.
Si representas los ingresos con la letra (I), el costo de la entrada con la letra (c), y el número de espectadores con la letra (n),
Tienes: I=c(n)
Y sabiendo que, para obtener la función que describe la relación del número de pesos que se reducen al costo de la entrada y el número de asistentes posibles, se puede obtener una expresión matemática, así que la plantearás en función de “x”, en donde x es la cantidad de pesos que se reduce al precio original de entrada.
Para ello, tienes que: - Video 7
https://youtu.be/ZTg4QpgZXxs
Observa ahora cómo utilizar la expresión anterior para saber cuánto se debe disminuir la entrada con el fin de obtener los 35,000 pesos que desea el director del club de teatro. - Video 8
Toda ecuación de segundo grado tiene dos soluciones para la incógnita, en este caso, observa cuál es la que conviene considerar para el problema.
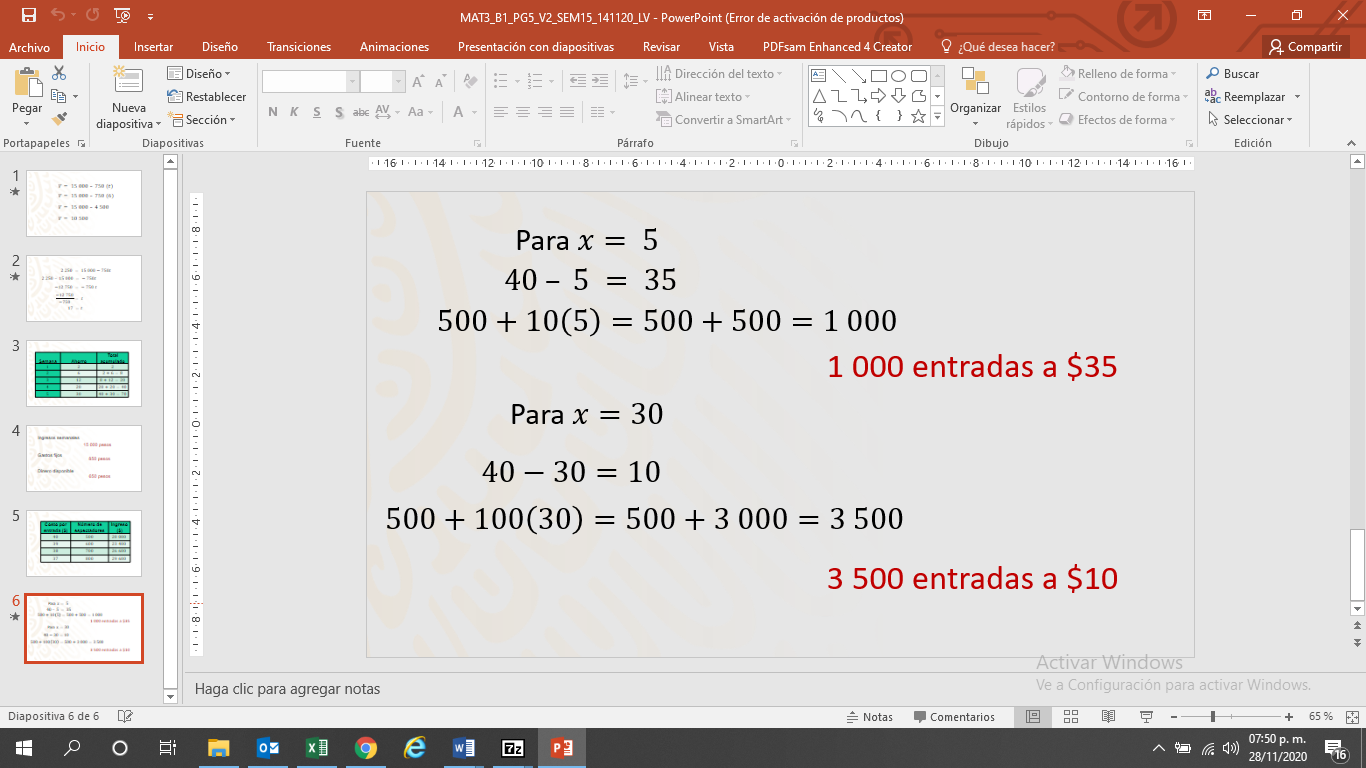
Tienes que para x = 5
El precio de la entrada al teatro será 40 – 5 =35
Lo que permitirá que entren a la función 500 + 100(5) = 500 + 500 = 1 000 personas.
Ahora, si consideras la solución en donde x = 30
Tienes para el costo de la entrada 40 – 30 = 10
Por lo que el número de personas será 500 + 100(30) = 500 + 3 000 = 3 500 personas.
Como verás, se tienen 1,000 entradas de 35 pesos cada una o 3,500 entradas de a 10 pesos cada una.
¿Qué conviene más?
El tesorero del club de teatro determina que es más conveniente, en este caso, recibir a 1,000 personas y cobrar la entrada de 35 pesos, que tener a 3,500 personas con entradas de 10 pesos, pues sabe que el teatro tiene una capacidad máxima de 1,500 personas.
Como observaste, los problemas vistos en esta sesión tienen su enfoque en la economía. Las tablas y las gráficas ayudan a observar los patrones que se siguen en las relaciones costo-beneficio, ahorro, o ingresos, entre otros.
Algunas de estas relaciones se expresan mediante funciones lineales, y otras con funciones cuadráticas, así que tienes diversidad en la forma de solucionar los distintos problemas que se pueden presentar.
El reto de hoy:
Trabaja este tema en tu libro de texto gratuito para que puedan resolver más problemas sobre lo estudiado en esta sesión.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas