¿Qué fracción es? II
¿Qué fracción es? II
Aprendizaje esperado: representación de fracciones de magnitudes continuas (longitudes, superficies de figuras). Identificación de la unidad, dada una fracción de la misma.
Énfasis: establecer relaciones entre las partes de una unidad, así como entre una parte y la unidad.
¿Qué vamos a aprender?
Aprenderás a establecer relaciones entre las partes de una unidad, así como entre una parte y la unidad. Propiamente identificarás y representarás fracciones propias e impropias en diversas figuras y longitudes.
¿Qué hacemos?
Identifica qué fracción representa cada pieza del tangram.
Para ello todo el tangram se considera la unidad. Está recortado porque si sobrepones algunas piezas, podrás resolverlo.
Te voy compartiendo un procedimiento que me sé y tú lo vas desarrollando, y así juntos lo resolvemos, ¿Te parece?
Primero, toma el tangram sin recortar.
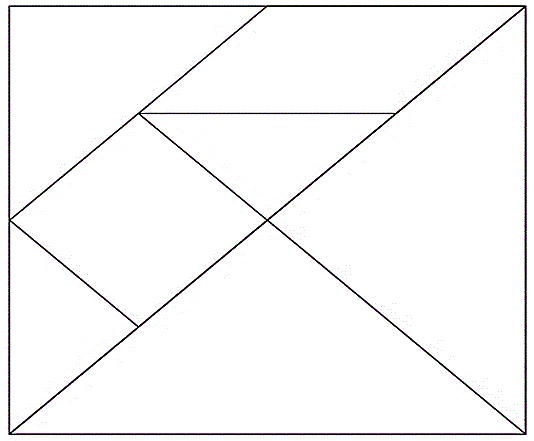
Ahora vas a doblarlo por la mitad sobre la línea diagonal que recorre todo el tangram. Dime, ¿Qué observas?

Se observan dos triángulos.
Eso quiere decir que los triángulos grandes equivalen a la mitad de tu tangram, es decir que juntos son ½. Pero como quieres saber qué fracción es sólo un triángulo, lo que harás es muy sencillo, vas a volver a doblar por la línea que divide a los dos triángulos, y te quedará un solo triángulo.
Ahora vas a desdoblar la figura y observas las marcas que han dejado los dobleces.
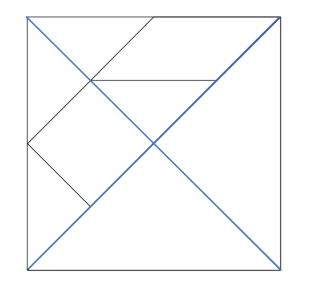
Para que los distingas en la imagen, se marcó en esta imagen los dobleces con color azul, ¿Cuántos triángulos como los grandes forman el tangram?
Claramente se pueden apreciar 4 triángulos grandes, esto quiere decir que cada triángulo es igual a ¼ de la imagen, vamos a anotar en cada triángulo grande la fracción ¼
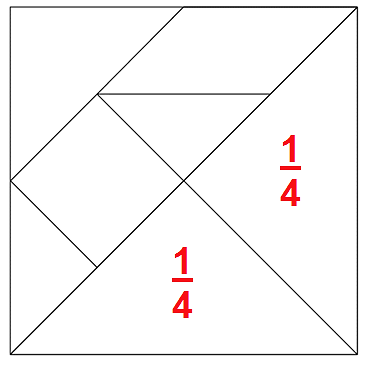
Si la parte donde se encuentra el cuadrado, la divides con una línea diagonal, este cuarto queda dividido en 4 triángulos de igual tamaño, los cuales están destacados en color en la figura de la derecha.


Entonces, puedes concluir que, si una cuarta parte de la imagen la conforman 4 triángulos, entonces la imagen completa tiene 16 triángulos.

Así que cada triángulo pequeño equivale a 1/16 es decir una parte de 16 por lo anterior, el cuadrado equivale a 2/16 al igual que el triángulo mediano y también el romboide porque de ese cuarto sólo están dos triángulos visibles y el romboide ocupa la superficie de dos triángulos.
Por lo que cada figura del tangram representa las fracciones siguientes:
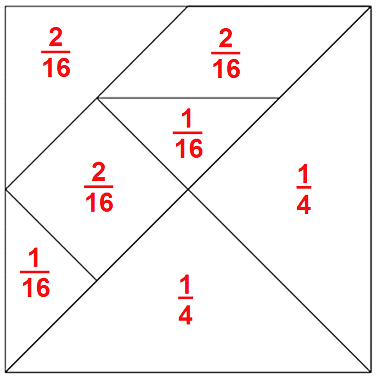
Para completar el trabajo, recuerda que puedes obtener fracciones equivalentes.
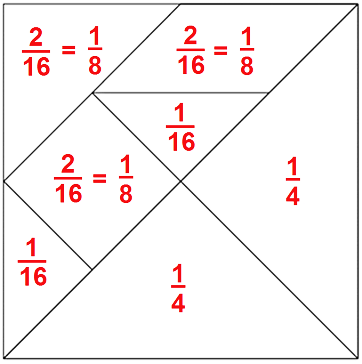
Por ejemplo, al descubrir que en una cuarta parte obtienes 4/16 entonces ¼= 4/16 en el caso de la fracción 2/16 puedes simplificarla dividiendo tanto el numerador y denominador entre dos y obtienes que nos da 1/8 es decir que 2/16 = 1/8 que es la superficie del triángulo menor, el cuadrado y el romboide.
Entonces si 4/16 lo simplificas como se hizo con 2/16 entonces también 1/4 = 2/8
Ya has terminado con tu reto. Déjame mostrarte, lo que has obtenido.

Observa la siguiente situación.
Diego y Daniela son diseñadores gráficos y les han pedido que elaboren en su trabajo un anuncio publicitario para una revista. La distribución de los elementos del anuncio es la siguiente:
- Una tercera parte será ocupada por una fotografía.
- Un sexto se destinará para información relacionada con el producto anunciado.
- En la cuarta parte del anuncio, en la zona superior derecha, aparecerá un texto relacionado con la fotografía.
- Un espacio, que corresponde a la sexta parte del anuncio, será destinado para una frase publicitaria.
- Finalmente, en un doceavo, se presentarán los datos para los procedimientos de compra.
Y esta es la imagen del prototipo o modelo del anuncio.

¿Cuáles serán las líneas que dividen la representación en tercios?
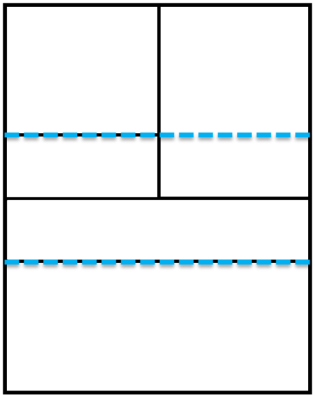
Claramente puedes apreciar las tres partes de manera horizontal. Ahora, ¿Cuáles son las líneas que señalan la cuarta parte del anuncio? ¿Podrías trazarla con color rojo, por favor?
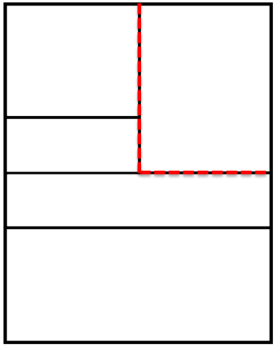
Claramente puedes apreciar una cuarta parte. Ahora, ¿Cuál es la sección que representa la sexta parte de todo el anuncio?

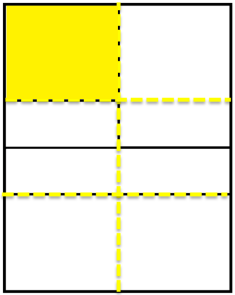
Claramente puedes apreciar la sección que representa la sexta parte. Ahora, ¿Cuáles serán las líneas que dividen la representación en doceavos?
Así queda.
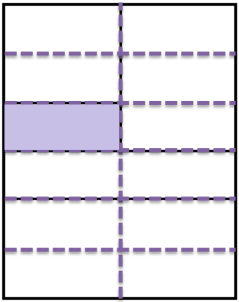
Para continuar aprendiendo realiza otra actividad.
Doña Martha tiene dos hijos que le ayudan a sembrar hortalizas en su casa; a cada uno le ha asignado un espacio para su cuidado.
Los cuadrados verdes representan cada uno de los espacios de terreno asignados a sus hijos, y los cuadrados naranja representan lo que cada uno ha sembrado de zanahoria en su respectivo terreno.
¿Qué fracción representa la parte que han sembrado entre los dos?

Si cada cuadro se considera un entero, entonces tienes que la imagen te muestra dos enteros.
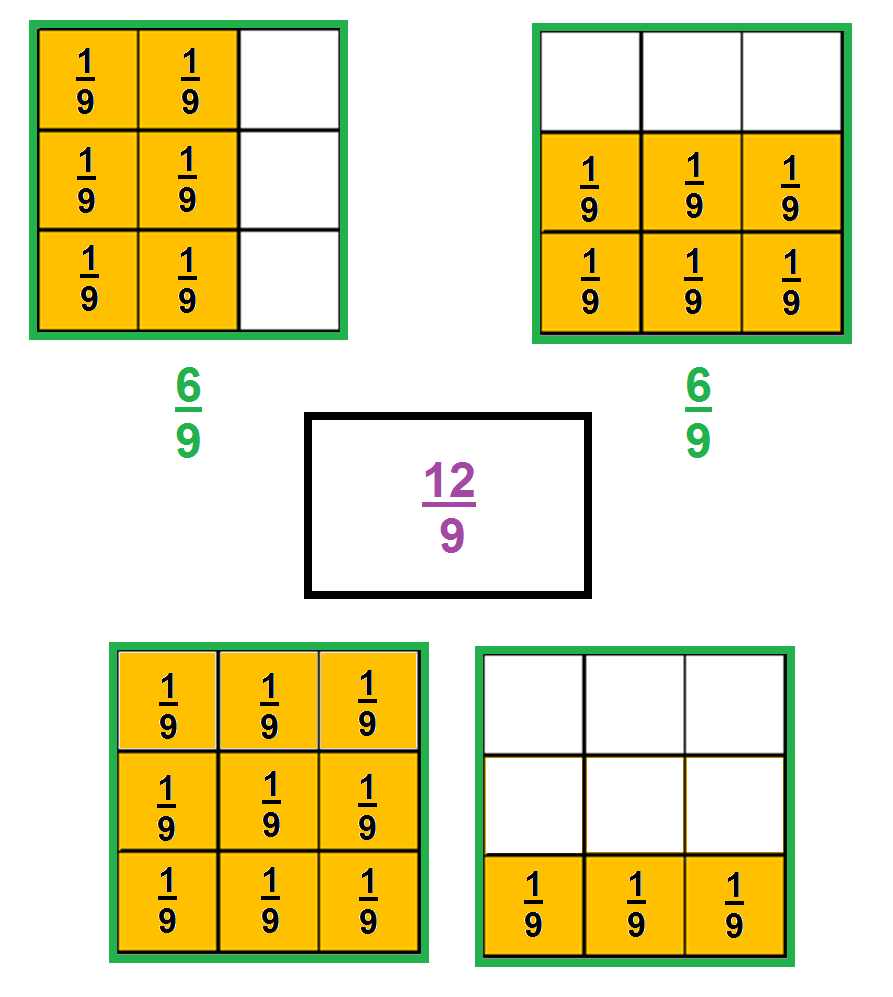
Ahora si cada entero se dividió en 9 partes, entonces tienes que 9/9 + 9/9 = 18/9 y, si del primer terreno se sembraron 6/9 y del segundo terreno también, se sembraron 6/9, tienes que entre ambos sembraron 6/9 + 6/9 = 12/9 o lo que es igual a un terreno entero con 3/9.
Ahora tienes los siguientes rectángulos que representan lo que han sembrado de lechuga.
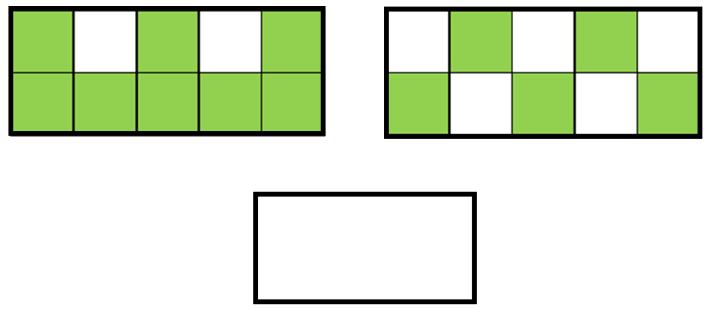
Si cada rectángulo cuadriculado se considera una unidad, ¿Qué fracción representa la parte que se sembró, la cual está pintada en verde?
Piensa nuevamente.
Si cada rectángulo se considera un entero entonces tienes que un entero + un entero = dos enteros.
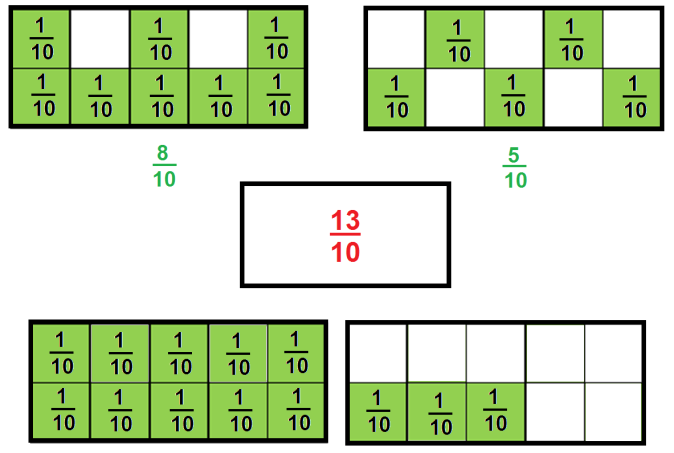
Ahora, si cada entero se dividió en 10 partes, entonces tienes que 10/10 + 10/10 = 20/10 y si del primer terreno mostrado a la izquierda se sembraron 8/10 y del segundo terreno mostrado a la derecha se sembraron 5/10 entonces la parte que han sembrado entre los dos hijos será 8/10 + 5/10 = 13/10 o lo que es igual a un terreno entero con 3/10.
Ahora identificarás algunas fracciones en algunos segmentos. Presta atención.
Si el segmento mayor, indicado con las letras AB, se considera una unidad, ¿Cuál es la fracción que representa cada uno de los segmentos menores?
Como apoyo, anota las medidas del segmento a considerar.
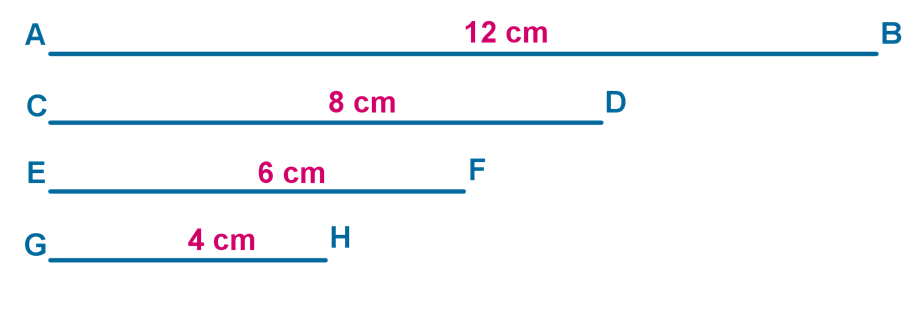
Si el segmento unidad tiene una longitud de 12 centímetros, ¿Qué tienes que hacer para saber qué segmento equivale a ½?
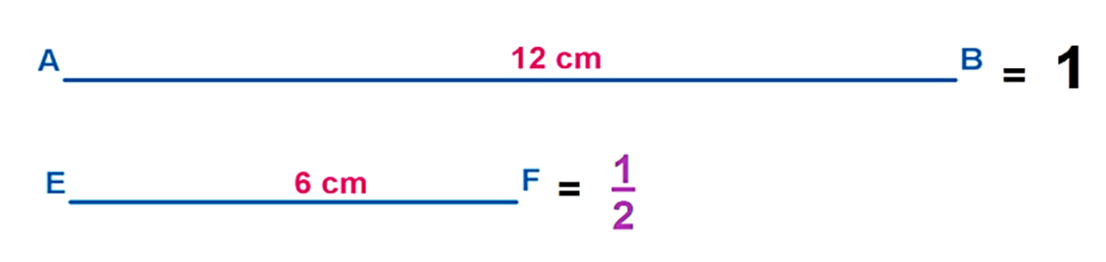
Pues tendrías que dividir esa medida entre dos, es decir 12 ÷ 2 = 6 y corresponde a la longitud del segmento EF de 6 centímetros. Ese segmento representa ½ del segmento unidad, y anotas la fracción enfrente de la imagen.
¿Qué tienes que hacer para saber que segmento equivale a 1/3?

Tendrías que dividir esa medida entre tres, es decir 12 ÷ 3 = 4 y corresponde a la longitud del segmento GH de 4 centímetros.
Lo que quiere decir que ese segmento representa 1/3 y anotamos la fracción enfrente de la imagen.
Por último, ¿Qué tienes que hacer para saber que fracción representa el segmento CD?
A simple vista es más de ½ pero para saber con exactitud podrías dividir el segmento CD en dos partes iguales, es decir 8 ÷ 2 = 4 y corresponde a la longitud del segmento GH. Entonces el segmento CD es dos veces el segmento GH, es decir 1/3 + 1/3 = 2/3
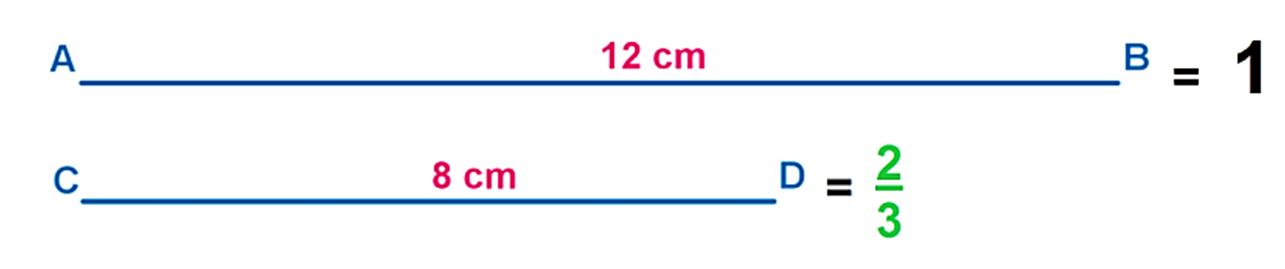
Lo que quiere decir que ese segmento representa 2/3 del segmento unidad, y anota la fracción enfrente de la imagen.
Has culminado este ejercicio, queda de la siguiente manera:

Para enfatizar lo que aprendiste en esta sesión:
Que, para establecer relaciones entre las partes de una unidad, así como entre una parte y la unidad, debes identificar cuántas partes forman esa unidad.
El reto de hoy:
Resuelve el desafío correspondiente al tema de tu libro de texto de Desafíos matemáticos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/