Múltiples representaciones algebraicas del área
Múltiples representaciones algebraicas del área
Aprendizaje esperado: formula expresiones de primer grado para representar propiedades (perímetros y áreas) de figuras geométricas y verifica su equivalencia en expresiones, tanto algebraica como geométricamente (análisis de las figuras).
Énfasis: formular conjeturas y validar las múltiples representaciones algebraicas del área de las figuras y establecer su equivalencia.
¿Qué vamos a aprender?
Conocerás nuevos significados, así como técnicas, procedimientos y algoritmos para resolver problemas. Para ello, llevarás a cabo una serie de hipótesis y validarás las múltiples representaciones algebraicas del área de las figuras, estableciendo sus equivalencias.
Debes saber que la comprensión de las fórmulas para el cálculo de la medida del área de las figuras geométricas es un proceso que requiere de tu participación activa. Al comprender un procedimiento también se construye un significado, en este caso, el significado de qué es el área de las figuras. No sólo son importantes los procedimientos sino los significados.
En esta sesión analizarás casos específicos para llegar a la generalización que constituyen las fórmulas geométricas. De esta manera, podrás aplicar las fórmulas a una gran diversidad de problemas que implican un cálculo del área.
¿Qué hacemos?
Reflexiona a partir de las siguientes preguntas, mismas que puedes registrar en tu cuaderno e ir respondiendo a lo largo de la sesión.
¿Cuál es la fórmula para calcular el área de un cuadrado y un rectángulo?
¿Qué se hace cuando se tienen que multiplicar dos variables?
¿Qué procedimiento debes realizar para verificar que la solución obtenida es correcta?
A continuación, analiza el primer problema para calcular el área de figuras geométricas.
Problema 1.
José quiere ampliar su granja para reacomodar a sus animales. El terreno de la granja se representa en color verde. José necesita comprar los terrenos que aparecen en color azul y amarillo.
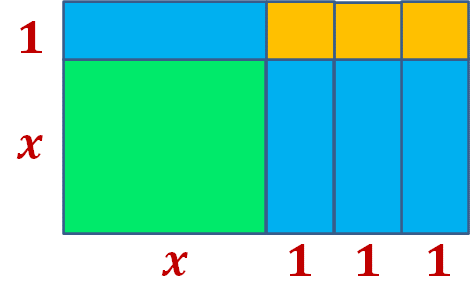
- ¿Qué forma tiene el terreno de José?
Tiene forma de cuadrado. - ¿Qué forma tienen los terrenos que necesita comprar?
Los amarillos tienen forma cuadrada, y los azules forma rectangular. - Al comprar los terrenos, ¿qué forma tendrá la granja?
La granja tendrá forma rectangular. - ¿Cuál es el ancho del rectángulo que representa el nuevo terreno?
El ancho del rectángulo también se le conoce como la altura, por lo tanto, se suma la altura del cuadrado verde más la altura del rectángulo azul; que se encuentra arriba del cuadrado verde. Entonces el ancho es igual a:
x + 1 - ¿Cuál es la medida del largo del terreno?
Al largo de un rectángulo también se le conoce como la base, en este caso, se suma la base del cuadrado verde más las tres bases de los rectángulos azules, obteniendo:
x + 3 - Escribe una expresión algebraica que represente el área verde.
(x)(x) - Escribe una expresión algebraica que represente el área de cada rectángulo azul.
(1)(x) - Escribe una expresión algebraica que represente el área de cada cuadro amarillo.
(1)(1) - Escribe la expresión algebraica que represente el área total del terreno.
Tomando en cuenta el cuadrado verde (x)(x), y como se tienen cuatro rectángulos azules se obtiene la siguiente suma:
(x)(x)+(1)(x)+(1)(x)+(1)(x)+(1)(x)+(1)(1)+(1)(1)+(1)(1) - ¿De qué otra manera se puede representar el área total del terreno?
Tomando en cuenta la figura total, se tiene como base (x + 3) por su altura (x + 1), es decir:
(x + 3) (x + 1)
Con estos datos, se puede responder a la primera pregunta que se hizo, al iniciar la clase, la fórmula para calcular el área de un cuadrado y de un rectángulo se deduce considerando la medida de la base y de la altura de la figura.
Base (x + 3) por su altura (x + 1)
Continúa con el segundo ejercicio.
Problema 2.
Establece tres expresiones algebraicas equivalentes que
representen el área de la figura.

Tomando en cuenta la figura total y la fórmula del área de un rectángulo, que es igual a base por altura, se obtiene la siguiente expresión:

Tomando en cuenta las figuras parciales se obtiene:
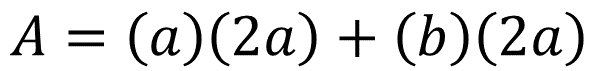
Si se lleva a cabo la multiplicación, se obtiene:
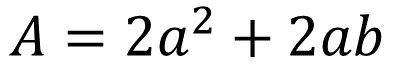
Has obtenido tres expresiones algebraicas equivalentes, y además se ha determinado el área de la figura.
Ahora, calcula el área de la siguiente figura.
Primero, analízala.
¿Cuántas figuras forman a la figura 1? ¿Cuáles son sus medidas?
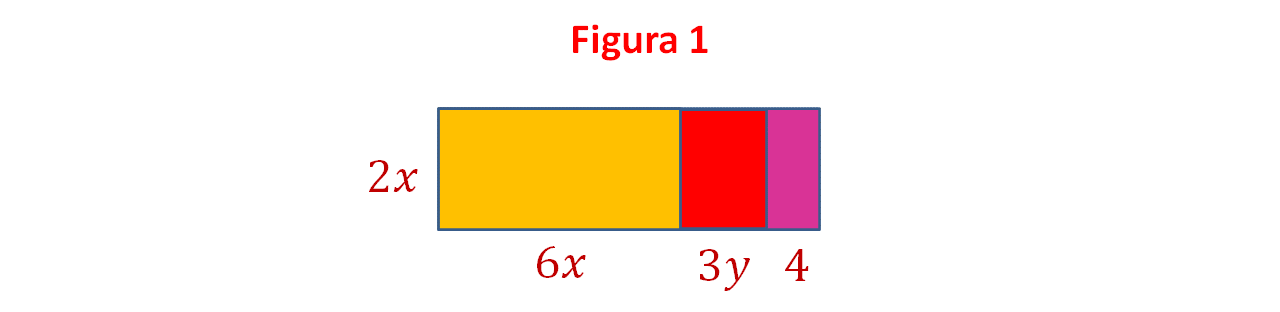
Son tres rectángulos: uno amarillo, uno rojo y uno rosa.
El rectángulo amarillo mide de base 6x; el rojo mide de base 3y; y el rectángulo rosa mide de base 4.
Tomando en cuenta la figura total y la fórmula del área de un rectángulo que es igual a base por altura, se obtiene la siguiente expresión:
El área de la figura es igual a la suma de los tres términos de la base (6x + 3y + 4) multiplicado por la altura de la figura que es igual a (2x). Por lo tanto:
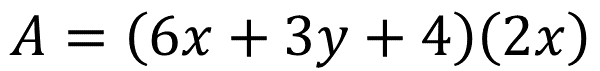
Tomando en cuenta las figuras parciales se obtiene:
El área de la figura total es igual a (6x) (2x), del rectángulo amarillo, más (3y) (2x) del rectángulo morado, más (4) (2x) del rectángulo rosa.
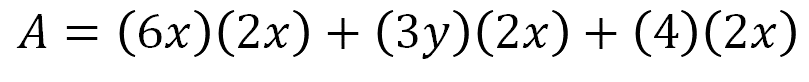
Si se lleva a cabo la multiplicación se obtiene:
El área es igual a 12x cuadrada + 6xy + 8x. Por lo tanto:
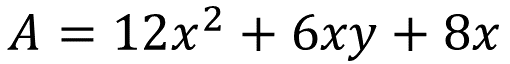
A continuación, realiza lo siguiente.
Calcula el área de otra figura.
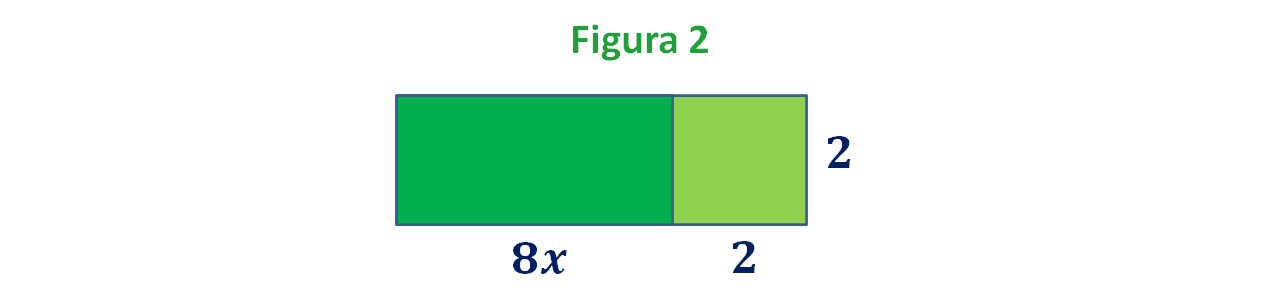
Tomando en cuenta la figura total y la fórmula del área de un rectángulo, que es igual a base por altura, se obtiene la siguiente expresión:
El área del rectángulo es igual a la base, (8x + 2) por su altura que tiene como valor (2). Por lo tanto:
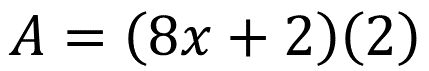
Tomando en cuenta las figuras parciales se tiene que el área del rectángulo es igual a (8x) (2) + (2) (2). Entonces:
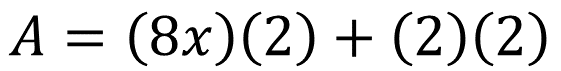
Si se lleva a cabo la multiplicación se tiene que el área es igual a:
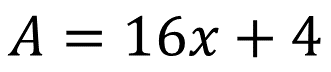
Acabas de establecer una expresión algebraica para calcular el área de una figura.
¿Con la ayuda de las expresiones algebraicas se puede obtener el área de una figura geométrica?
Para responder a esta pregunta observa el siguiente ejemplo, cuyo propósito es mostrar cómo obtener el área algebraica de una figura geométrica.
Problema 3.
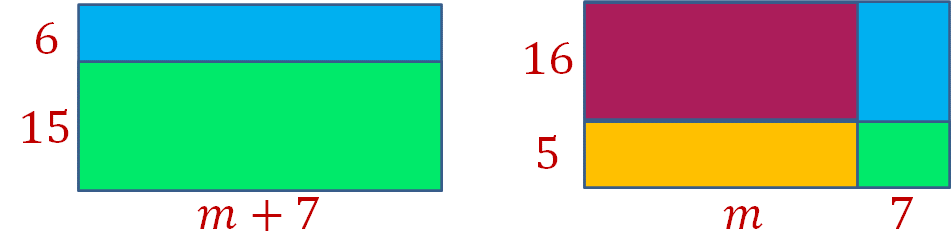
Los rectángulos P y Q son congruentes. ¿Qué expresiones algebraicas representan las áreas de cada figura? Escríbelas.
Recuerda que en el área de un rectángulo se utiliza la siguiente formula:
Área = base x altura
Por lo tanto:
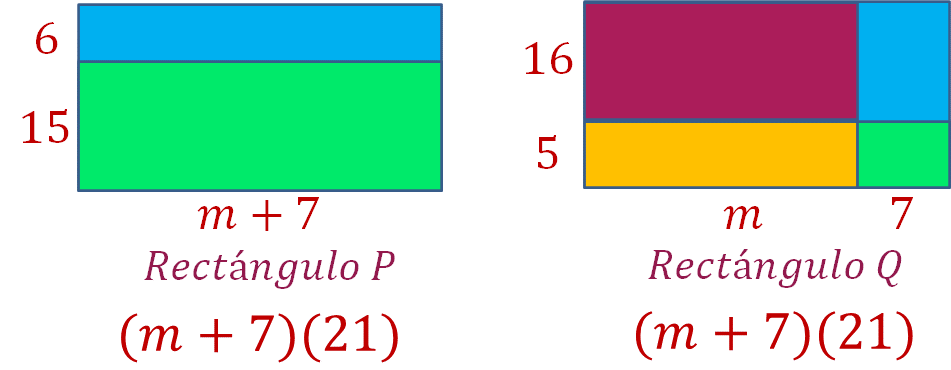
¿Son equivalentes las expresiones algebraicas que representan el área de los rectángulos P y Q?
Comprueba con el rectángulo “P”. Para llevarlo a cabo, suma ambas áreas de los rectángulos. Comienza con el rectángulo verde, su base es “m + 7 (15)” y suma el área del rectángulo azul, su base es: (m + 7) (6). Realiza las operaciones y suma los términos semejantes:

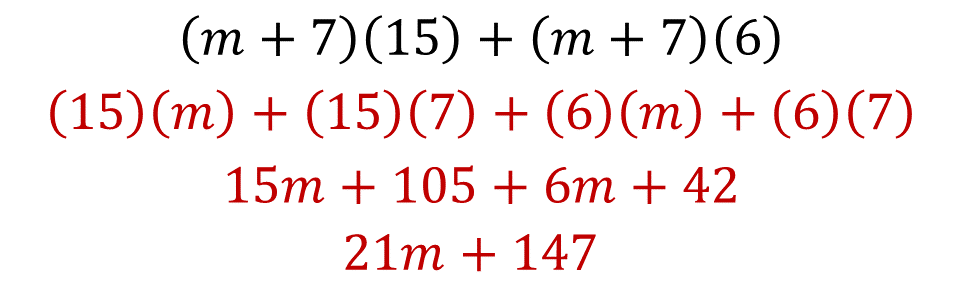
Ahora, comprueba el rectángulo “Q”, con el mismo procedimiento del rectángulo anterior. En este caso, sumarás el área de los 4 rectángulos:

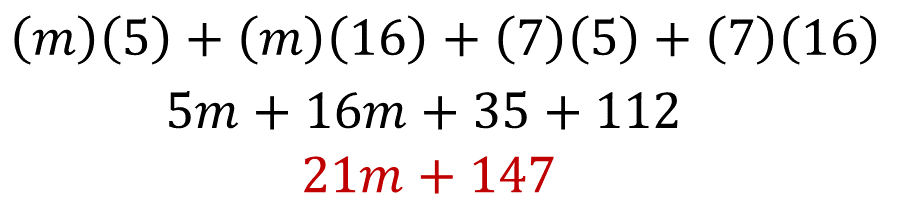
Por lo tanto, se comprueba que son equivalentes las expresiones algebraicas que representan el área de los rectángulos P y Q, ya que realizar la expresión algebraica se obtienen los mismos términos semejantes, tanto del rectángulo “P” como en el rectángulo “Q”.

Analiza el siguiente problema.
Problema 4.
¿Qué expresiones algebraicas representan las áreas de la siguiente figura?
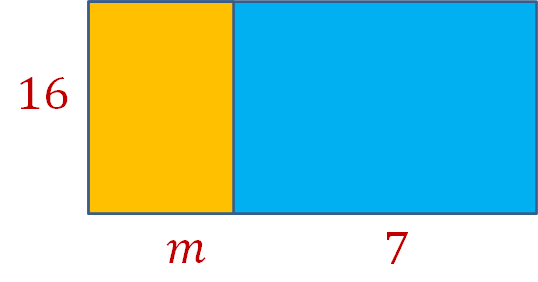
Responde las siguientes preguntas:
- El área del rectángulo como largo por ancho
(m + 7) (16) - El área del rectángulo como la suma de las áreas de los rectángulos que lo forman.
(m) (16) + (7) (16)
¿Ambos resultados son equivalentes?
(m + 7) (16) = (m) (16) + (7) (16)
16m + 112 = 16m + 112
Resuelve la siguiente situación, donde repasarás una de las tres leyes de los exponentes.
Escribe en cada recuadro el término faltante.
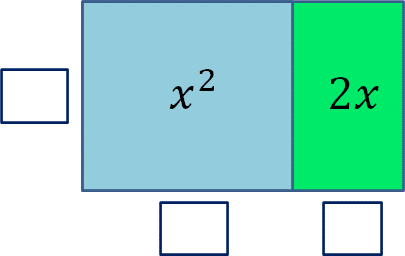
- ¿Cómo se obtienen los términos faltantes de la figura azul?
Tomando en cuenta que se trata de un cuadrado, y sus lados son iguales, por lo tanto, se dice que un lado vale “x”, porque si se multiplica “x” por “x” es igual a “x” elevado al cuadrado. - ¿Cómo obtuviste el término faltante de la figura verde?
La altura del cuadrado es igual a “x”, entonces la base del rectángulo verde tiene que valer 2. Porque 2 por “x” es igual a “2x”. - ¿Cuál es el área total de la figura?
Sumando los dos términos, la del cuadrado azul más el rectángulo verde resulta, “x” elevado al cuadrado más “2x”.
Profundiza más en el tema y en qué son las expresiones equivalentes.
Expresiones equivalentes
Dos o más expresiones algebraicas son equivalentes si representan la misma cantidad, es decir, si tienen el mismo valor numérico.
Una expresión también es equivalente cuando se realiza una transformación algebraica, al reducir o agrupar términos semejantes.
Compruébalo.
Calcula los valores de las siguientes expresiones algebraicas, si x = 5.
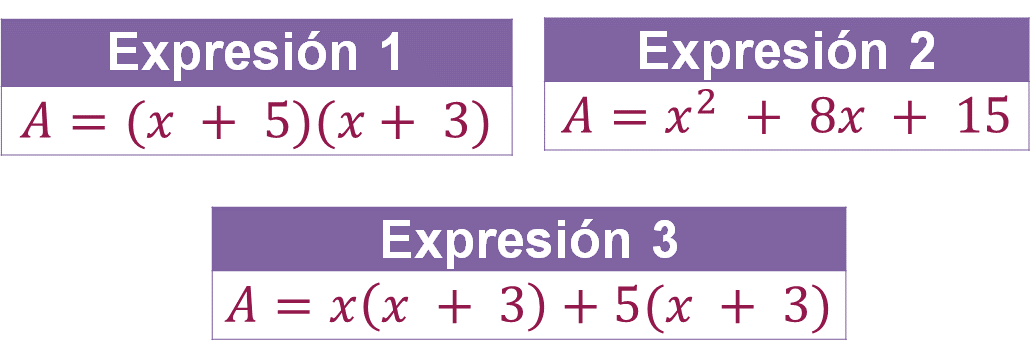
Ahora, comprueba si las siguientes expresiones son equivalentes.

Por lo tanto, “A” es igual a 80.

Por lo tanto, “A” es igual a 80.

Por lo tanto, “A” es igual a 80.
Una vez que se calculó el valor numérico de cada expresión al establecer el valor de x = 5, se observa que en todas se obtuvo el mismo resultado, por lo que se puede concluir que estas expresiones son equivalentes.

Ya puedes calcular el área algebraica de una figura geométrica. Puedes identificar cuándo tendrás que utilizar la ley de los exponentes, o qué hacer cuando tienen dos variables diferentes.
En esta sesión estudiaste expresiones algebraicas equivalentes para calcular el área algebraica de una figura geométrica, en este proceso llevaste a cabo el producto de dos términos con diferentes literales, y también la multiplicación de dos términos con literales iguales.
Consulta tu libro de texto de Matemáticas de segundo grado, seguramente encontrarás otras actividades que te ayudarán a profundizar en este tema.
El reto de hoy:
Ejercicio 1
Selecciona las expresiones algebraicas que representen el área total del rectángulo.
- xy + xz + 5
- x (y + z + 5)
- xy + xz + 5x
- x + y + z 5
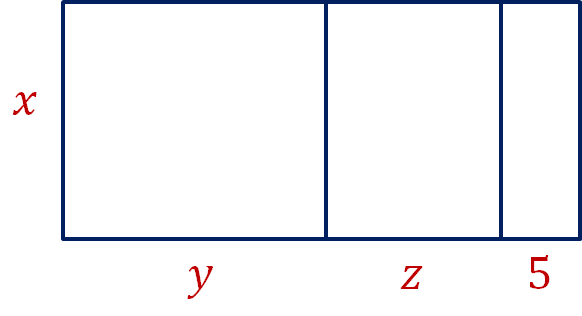
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas