Décimos, centésimos y milésimos. Las fracciones decimales
Las fracciones decimales
Aprendizaje esperado: notación desarrollada de números naturales y decimales. Valor posicional de las cifras de un número.
Énfasis: determinar fracciones decimales y establecer comparaciones entre ellas a partir de la división sucesiva en 10 partes de una unidad.
¿Qué vamos a aprender?
Aprenderás sobre las fracciones decimales y a establecer comparaciones entre ellas, a partir de la división sucesiva en 10 partes de una unidad.
En la sesión anterior aprendiste lo que es un décimo, un centésimo y un milésimo. Para recordarlo, responde las siguientes preguntas en tu cuaderno. Apóyate en la siguiente imagen, considerando que el cuadrado verde representa la unidad.

- ¿Qué es más grande, un décimo coloreado en azul o un centésimo coloreado en rojo?
- ¿Cuántas veces cabe un décimo en la unidad?
- ¿Cuántas veces cabe un centésimo en la unidad?
- ¿Cuántas veces cabe un milésimo, que es la parte marcada de menor tamaño?
- ¿Por qué crees que el décimo se llama así?
- ¿Cuántas veces cabe un centésimo en un décimo?
- ¿Qué parte de un décimo es un centésimo?
- ¿Qué parte de un centésimo es un milésimo?
Al final de esta ficha podrás encontrar las respuestas a estas preguntas, pero trata de contestarlas por ti mismo.
Si tienes libros en casa relacionados con el tema, o Internet, explóralos para saber más.
¿Qué hacemos?
Identifica en cada una de las siguientes imágenes, la fracción decimal que representa la parte sombreada. Analiza los que ya están resueltos.
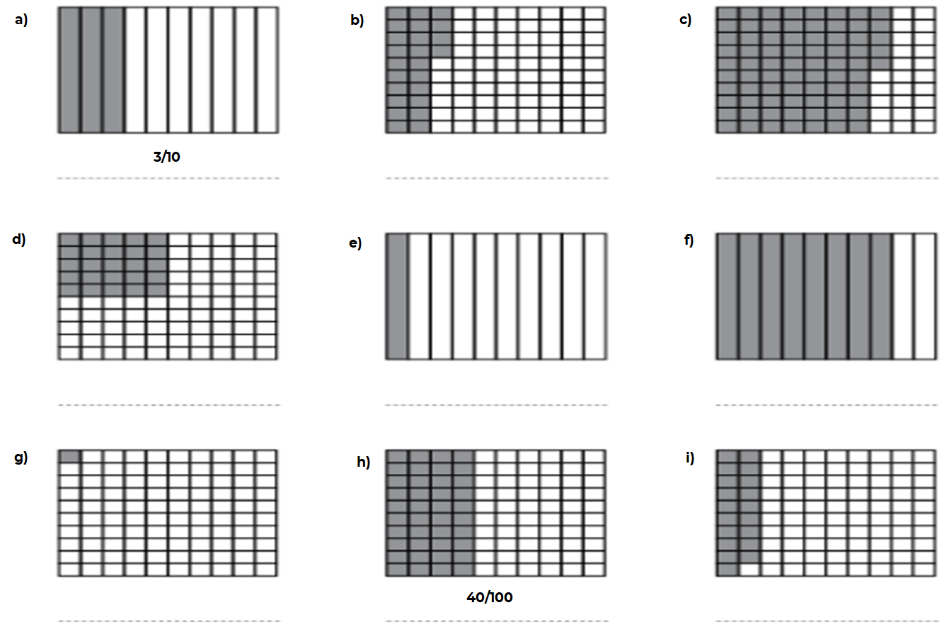
En la imagen a), están pintadas solamente 3 partes de 10, por lo que la fracción decimal es 3/10, ¿Cómo lo escribirías con un número decimal?
3/10 = 0.3
Recuerda que cuando la unidad se divide en 10 partes iguales, cada parte es un décimo. Se escribe 0.3 porque, después del punto indicamos que son tres partes de un total de 10, las que estamos tomando en cuenta. El 3, indica las tres partes sombreadas de la unidad.
Cualquiera de las dos formas de escritura, con fracción o con número decimal, se lee como tres décimos y representan la misma cantidad sombreada del cuadrado.
Ahora observa la imagen c), están pintadas solamente 75 partes de 100, ¿Cómo quedaría representada mediante una fracción esta cantidad, y en número decimal?
Quedaría como:
75/100 = 0.75
Cuando la unidad está dividida en cien partes, a cada parte se le llama centésimo. En este caso, son 75 partes de cien las que están sombreadas. Cuando escribes esa cantidad como número decimal, después del punto debes escribir el 75 que indica las partes sombreadas de la unidad.
En la imagen h), están pintadas 40 partes de 100, ¿Cómo quedaría representado en fracción y en número decimal?
40/100 = 0.40
Si la unidad está dividida en cien partes, entonces son centésimos. Si escribes esta cantidad como un número decimal, entonces después del punto debes escribir el 40, que indica las partes sombreadas de la unidad de un total de 100.
Analiza con atención la siguiente pregunta:
Si en lugar de escribir 0.40, se escribe 0.4, ¿Qué cantidad está escrita?
0.4, escrito como fracción decimal es: 4/10
Observa la siguiente imagen, para comprender mejor:
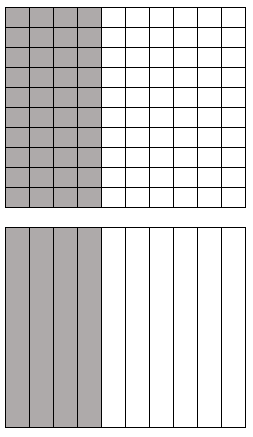
Si observas, el cuadrado donde están sombreados 40/100 equivale a un cuadrado donde están sombreados 4/10.
Esto quiere decir que tanto la fracción 40/100 como 4/10 representan la misma superficie, por lo que estas dos fracciones, son equivalentes.
4/10 = 40/100
0.4 = .40
Este conocimiento permite comprender y utilizar una propiedad muy útil e importante de los números decimales, la cual nos indica que:
Después de la última cifra significativa (cifra diferente de cero) a la derecha del punto decimal, pueden agregarse ceros sin que el decimal cambie de valor.
Por ejemplo:
En el número 0.340, la última cifra significativa es 4, por lo tanto, si yo escribo.
| 0.34 | |
| 0.340 | Todas son equivalentes |
| 0.3400 |
Para concluir, analiza lo siguiente.
Si la unidad que vas a dividir es UN METRO:
Un decímetro, es igual a 1/10 o 0.1 m
Un centímetro, es igual a 1/100 o 0.01 m
Un milímetro es igual a 1/1000 o 0.001 m
Ahora es tiempo de que compruebes si contestaste correctamente las preguntas que se plantearon al inicio de la sesión.

El reto de hoy:
En el siguiente rectángulo, dividido en 1000 pequeños rectángulos iguales, representa con distintos colores las siguientes cantidades:


Platica con tu familia sobre lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas