Triángulos congruentes

Aprendizaje Esperado: analiza la existencia y unicidad en la construcción de triángulos y cuadriláteros, y determina y usa criterios de congruencia de triángulos.

Énfasis: aplicar los criterios de congruencia para identificar triángulos congruentes.

¿Qué vamos a aprender?

En esta sesión aplicarás los criterios de congruencia para identificar triángulos congruentes.

Para esta sesión necesitarás tu cuaderno o papel para tomar notas, así como tu lápiz o pluma, goma, sacapuntas, tijeras y un juego de geometría con regla, compás, escuadras y transportador. Si tienes una discapacidad visual prepara tus hojas leyer, punzón y regleta.

¿Qué hacemos?

Seguramente en tu vida cotidiana has notado que existen objetos que tienen figuras o formas que se llegan a parecer entre sí, algunas de ellas son idénticas en su forma, pero su orientación suele ser distinta.

Como se mencionó en el propósito de la sesión, hoy se aplicarán criterios de congruencia. Para ello, se establecerá en primer lugar qué es la congruencia en figuras geométricas.

Se definirá a dos figuras congruentes como aquellas que poseen las mismas dimensiones y la misma forma sin importar su posición u orientación.

Un ejemplo muy común de congruencia se da en las llaves que usas en casa. Si en algún hogar existen más de un habitante seguramente necesitarán dos o más copias de la llave para poder ingresar a la vivienda. Estas llaves deben ser idénticas, es decir, congruentes entre sí, de lo contrario no podrían abrir el mismo cerrojo.

¿Qué te parece si se continua esta sesión con un problema matemático para desafiar tus conocimientos, acerca de la construcción de triángulos e identificación de figuras geométricas?

Se te invita a que realices las construcciones que se te van a sugerir.

Se comenzará por construir algunos triángulos, tú en casa puedes seguir la actividad. Se te darán algunas medidas específicas y podrás darte cuenta si obtienes triángulos congruentes entre sí. ¿Lista o listo?

Para el primer triángulo que vas a construir, los lados deben medir 10 cm, 12 cm y 8 cm.

Una compañera tuya llamada Lili comenzó la construcción utilizando el lado de 8 cm, para obtener su figura. A diferencia de Marcos que el comenzó su construcción a partir del lado que mide 10 cm.

¿Cuál fue el triángulo que obtuviste, en casa, para este ejemplo?

Ahora, se comprobará si los triángulos son iguales o congruentes entre sí. Para ello, se puede sobreponer uno encima del otro y la figura debe coincidir en su totalidad. Ésta es una forma muy pragmática de realizar la comprobación.

En el caso de Lili y Marcos lograron obtener dos triángulos congruentes.

¿Por qué piensas que se dio la congruencia de los triángulos?

Como siguiente ejemplo se debe construir un triángulo que posea dos lados de 5 cm y que el ángulo que se encuentra entre estos lados sea de 127º.

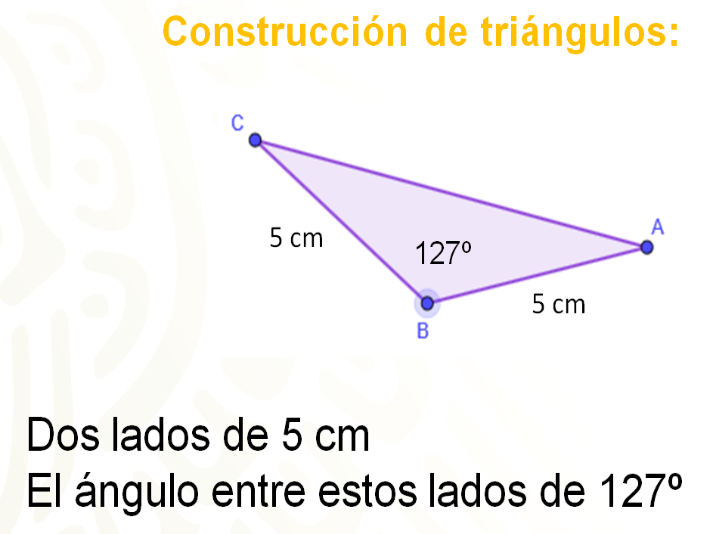
Ahora, el resultado de los triángulos obtenidos será de manera digital.

La siguiente imagen, muestra los triángulos que trazaron Lili y Marcos. En esta ocasión, en lugar de sobreponer los triángulos, los midieron para comprobar que sí son congruentes. Es decir, se midieron los lados de ambas figuras al igual que los ángulos.

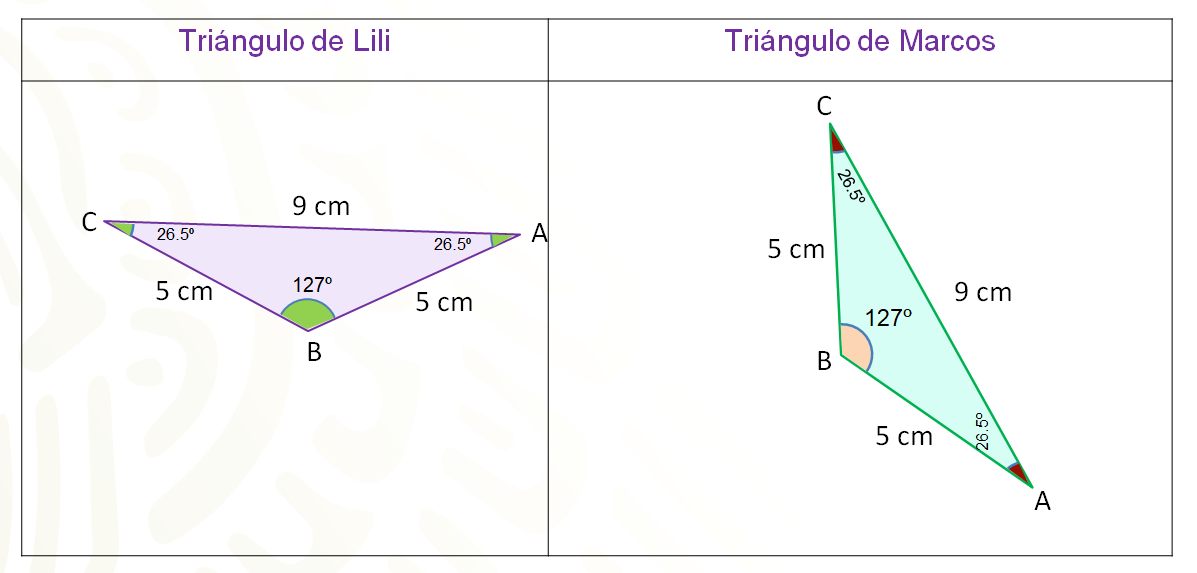
El triángulo que obtuvo Lili, con la indicación dada, mide 5 cm, 5 cm y el tercer lado mide 9 cm. Los ángulos miden 127º, y parece ser un triángulo isósceles, los otros ángulos miden 26.5º, cada uno, si se suman, se puede comprobar que da como resultado 180º.

En el caso de Marcos, las medidas de los lados de su triángulo son las mismas: 5 cm, 5 cm y 9 cm y sus ángulos miden 26.5º, 26.5º y 127º.

Entonces como los lados y los ángulos son iguales, se tienen nuevamente dos triángulos congruentes.

Con relación a lo anterior, reflexiona sobre las siguientes preguntas:

• ¿Fue necesario dar todas las medidas para determinar que los triángulos eran congruentes?
• ¿Qué información hubiera sido suficiente para establecer la congruencia?

Seguramente en casa ya tienes las respuestas.

Por último, se trazará un triángulo cuyas medidas sean: 45º, 53º y con un lado intermedio a estos ángulos que mida 7 cm.

El resultado que obtuvo Lili, de esta prueba fue el siguiente:

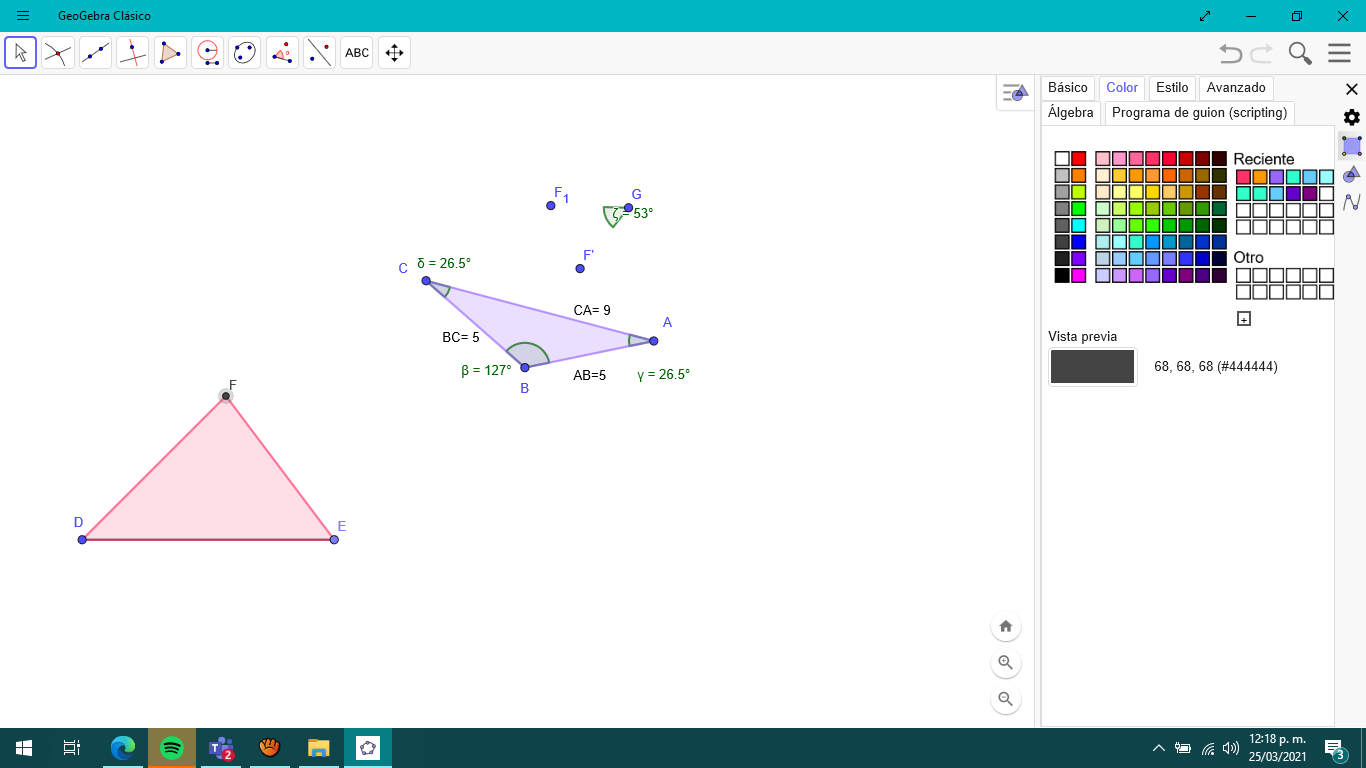
En el caso de Marcos, su triángulo es este.

A simple vista parecieran ser triángulos diferentes, pero hay que tomar las medidas necesarias para validar si son congruentes.

Al medir los lados de la figura de Lili, son 7 cm, 5 cm y 5.6 cm mientras que sus ángulos miden 82º, 53º y 45º.

Nuevamente los datos concuerdan debido a que las medidas de los lados del triángulo de Marcos son 5 cm, 7 cm y 5.6 cm; al igual que los ángulos, cuyas medidas son las mismas que las que tiene Lili. Así se obtuvieron triángulos congruentes.

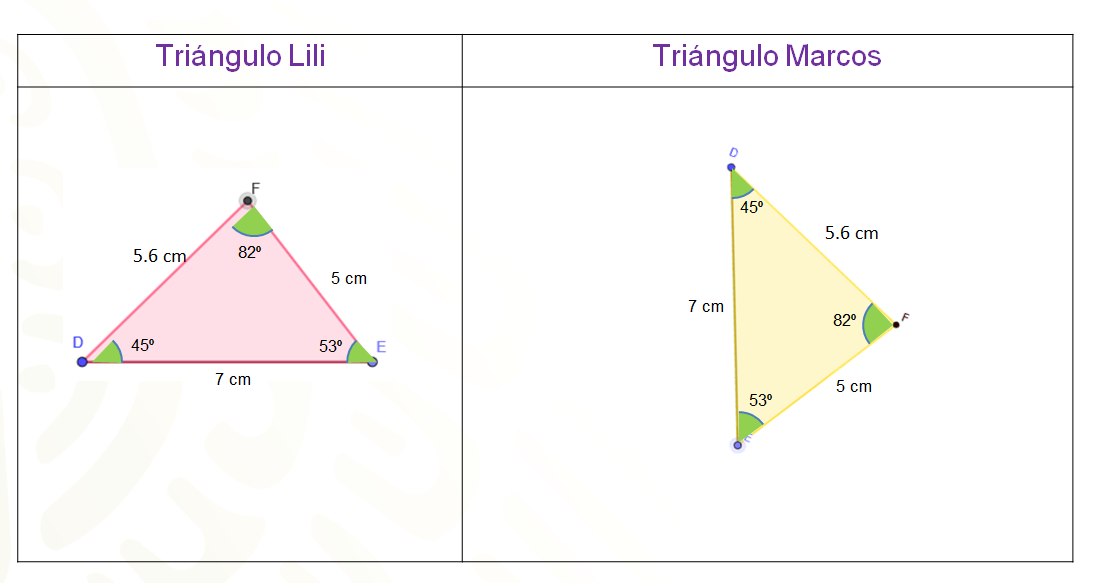
¿Piensas que es posible construir algún triángulo diferente a estos con los mismos datos proporcionados?

Para determinar si dos triángulos son congruentes, se pueden sobreponer las figuras o medirlas, como se hizo en las actividades previas. Pero no siempre se tiene la posibilidad de sobreponer las figuras o medirlas como se hizo en esta sección.

La opción más formal para establecer la congruencia de dos triángulos es a través de criterios que se basan en determinados datos proporcionados para su construcción ¿Ya conoces estos criterios?

Ahora, revisarás algunos de estos criterios, para formalizar la actividad anterior.

Antes de comenzar con los criterios se debe establecer el lenguaje matemático.

Se tiene un triángulo el cual posee las letras A, B y C en sus vértices, por lo que se le llamará triángulo ABC. Cada uno de los lados se nombrarán utilizando las letras de los vértices que delimitan cada lado. De esta manera, se puede establecer que el triángulo está compuesto por los lados AB, BC y CA la línea arriba de la letra mayúscula indica que se está hablando de un segmento.

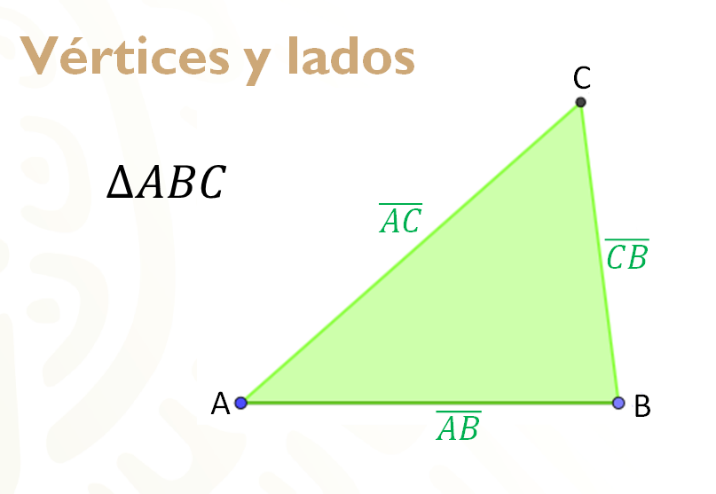
Para expresar un ángulo interno se utiliza el siguiente símbolo de abertura.

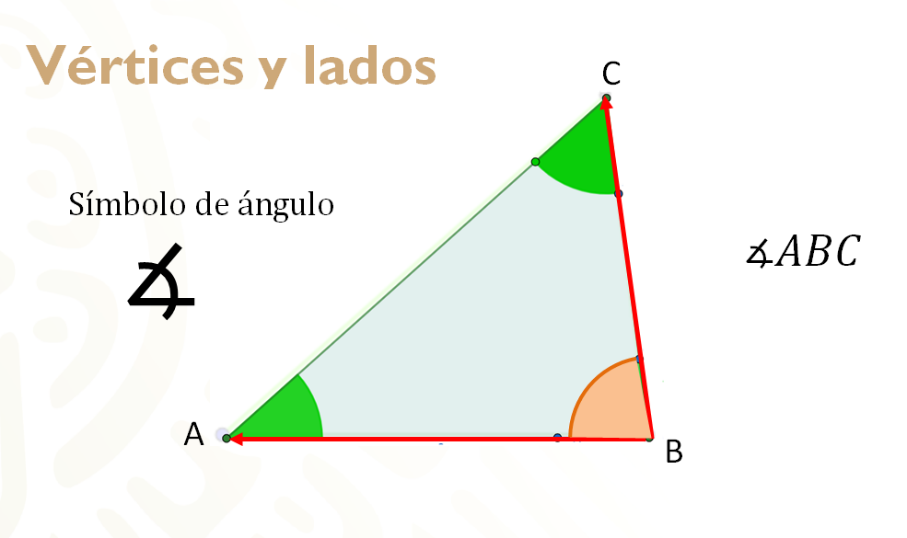
Para nombrar el ángulo interno del triángulo se nombran en sentido contrario a las manecillas del reloj, siendo las letras de la orilla los segmentos del ángulo y la letra intermedia el vértice. Como se muestra en el ejemplo del ángulo ABC.

Para establecer la congruencia entre los dos triángulos se utilizará el siguiente símbolo, que es muy similar al signo de igual, pero posee una tercera tilde de forma ondulada.

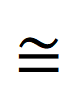
Ya con esta información se pueden analizar los criterios de congruencia de triángulos.

Como recordarás, para trazar el primer triángulo, se tomó como base la medida de los tres lados y se obtuvieron triángulos congruentes, sin necesidad de conocer la medida de los ángulos. Éste es el primer criterio.

El criterio es lado, lado, lado; expresado también como LLL, que indica que las tres parejas de lados correspondientes poseen la misma medida.

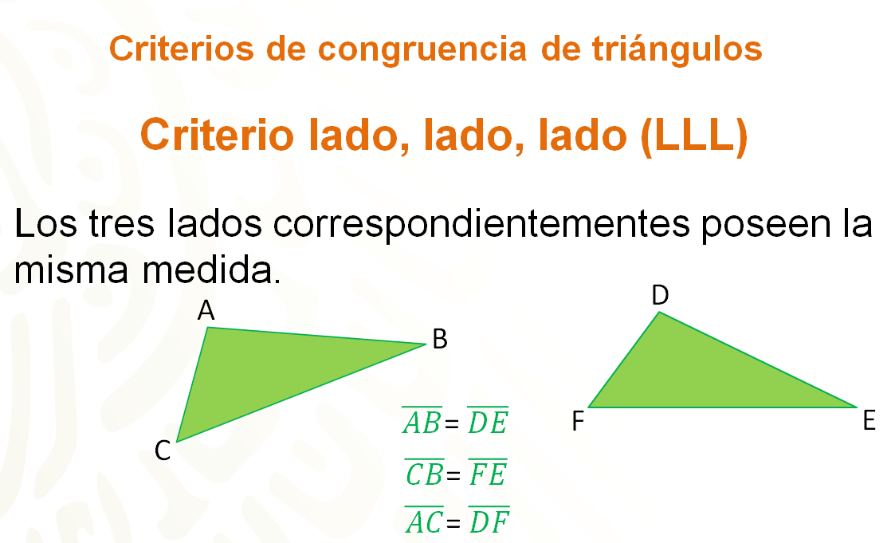
En el siguiente ejemplo, se tienen las medidas de los lados 10, 12 y 8, y se nombrará a cada uno de los vértices de los triángulos con letra mayúscula. El primer triángulo es ABC, mientras que al segundo triángulo se le dará el nombre DEF.

El triángulo 1 posee el segmento AB que mide 10, y tiene la misma medida al segmento DE del triángulo 2. De esta manera se establece que el segmento AB es congruente al segmento DE.

Así mismo, el segmento BC mide 8, al igual que el segmento FE del triángulo 2. Entonces el segmento BC es congruente al segmento FE.

Por último, el lado CA mide 12, el cual es congruente con el lado FD del triángulo 2, cuya medida también es 12.

Ahora que se estableció que los tres lados son congruentes, se puede decir que el triángulo 1 y el triángulo 2 son congruentes entre sí.

El segundo criterio de congruencia de triángulos hace referencia al lado, ángulo, lado; expresado como LAL.

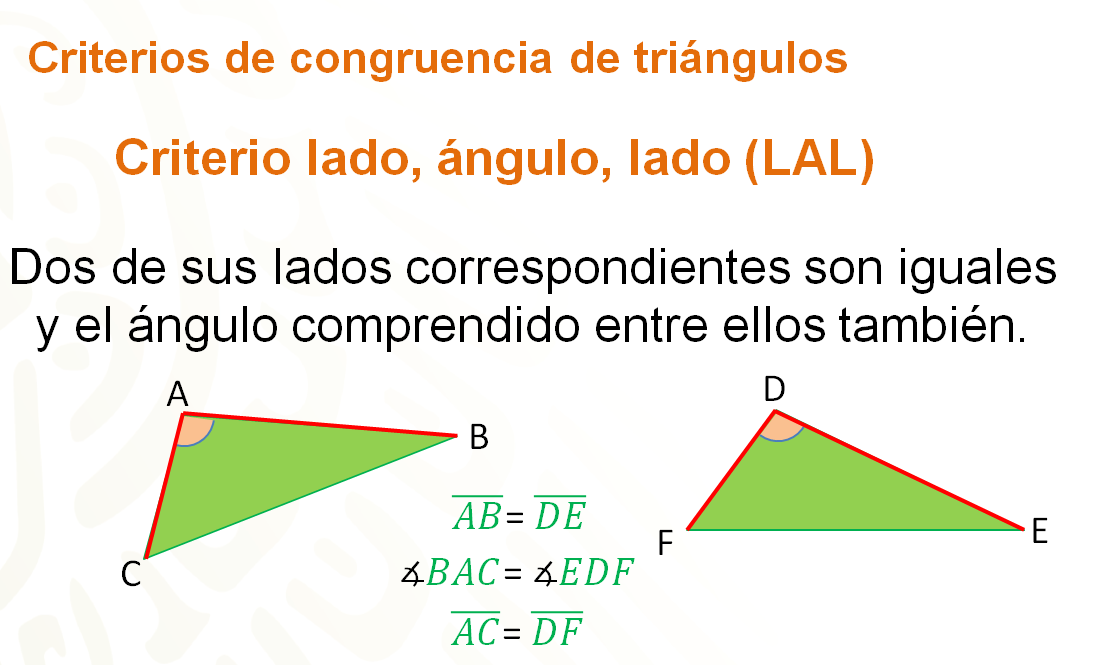
Se refiere a que dos triángulos son congruentes si dos de sus lados correspondientes son iguales y el ángulo comprendido entre ellos también lo es.

Para la segunda construcción se consideraron dos lados de 5 y un ángulo entre ellos de 127º.

Para demostrar la congruencia de ambos triángulos por medio de este segundo criterio. Se nombrará a los vértices del triángulo 3 con las letras GHI y al triángulo 4 con las letras JKL.

El lado GH mide 5, al igual que el lado JK. De la misma medida se tiene el lado HI y el lado KL de 5. Por lo tanto, el lado GH es congruente al lado JK, al igual que el lado HI es congruente a KL.

El ángulo GHI, que mide 127º es congruente al ángulo LKJ del triángulo 4.

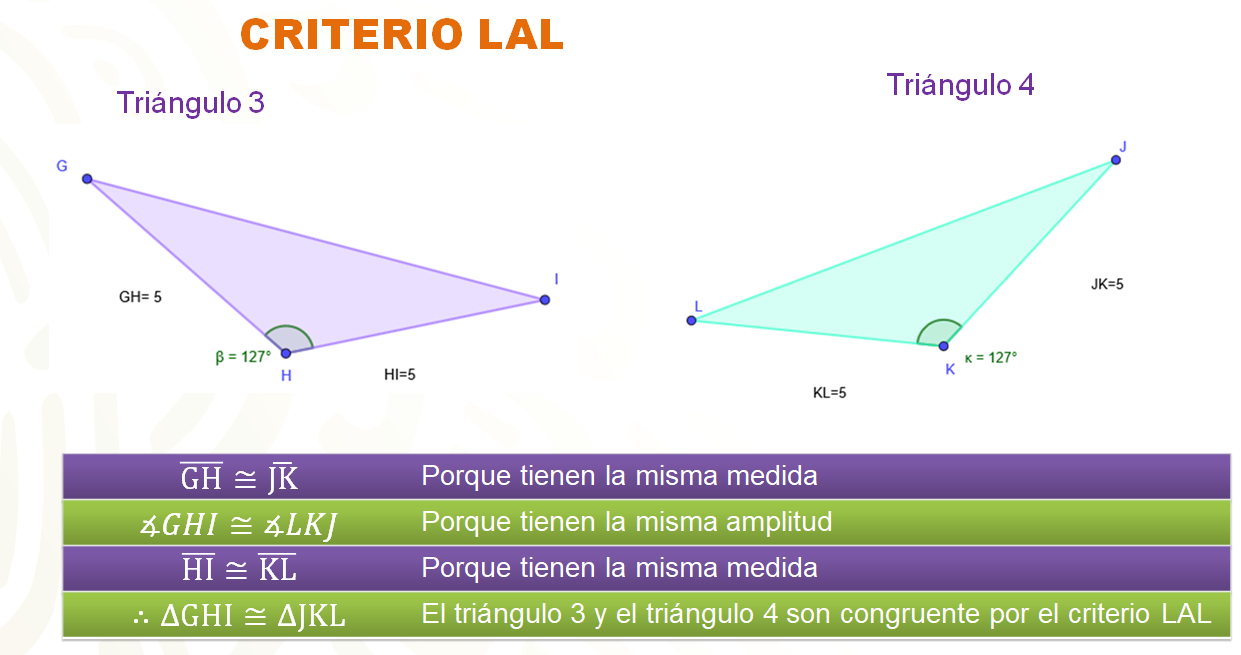
Se ha establecido la congruencia entre dos lados de cada triángulo y el ángulo formado por estos lados, por lo tanto, se puede establecer que el triángulo GHI es congruente al triángulo JKL.

El tercer criterio es ángulo, lado, ángulo; que se representa como ALA, el cual enuncia que: Dos triángulos son congruentes si dos de sus ángulos correspondientes son iguales y el lado comprendido entre ellos también es igual.

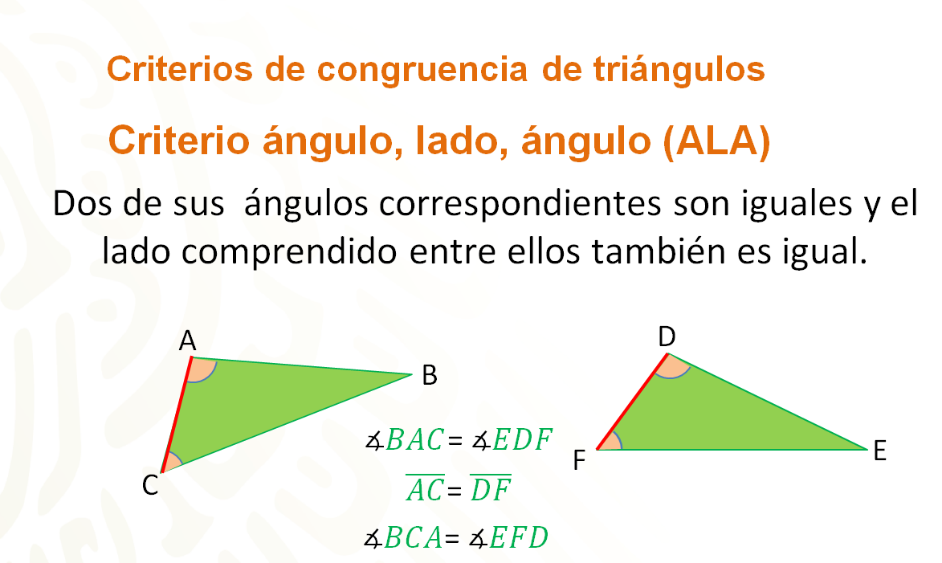
En este último ejemplo se trazó un triángulo cuyos ángulos miden 45º, 53º y con un lado entre ellos que mide 7.

Se nombrará al triángulo 5 y se identificará con las letras MNO y al triángulo 6 con las letras PQR.

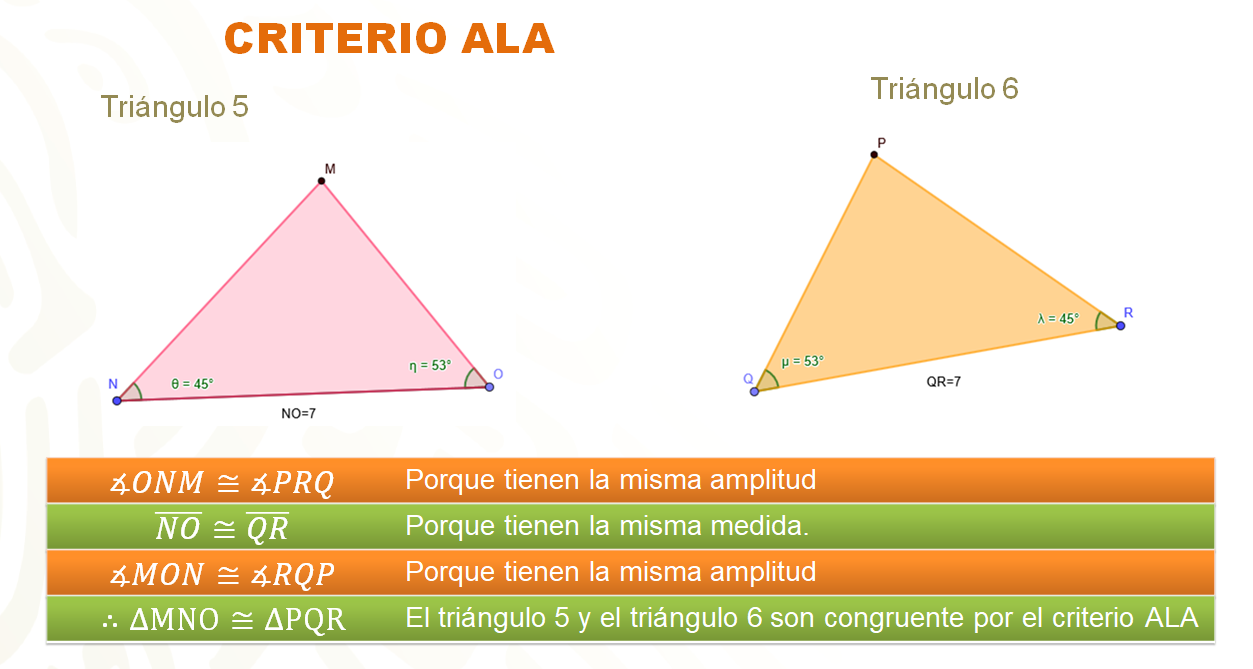
El ángulo ONM es congruente al ángulo PRQ debido a que ambos miden 45º.

De igual manera, el ángulo MON es congruente con el ángulo RQP, porque ambos miden 53º.

Por último, los lados NO y QR miden 7 y se ubica en medio de ambos ángulos.

Justificado lo anterior, se establece que el triángulo MNO y PQR son congruentes por el criterio ángulo, lado, ángulo.

Ahora que ya se retomaron los criterios de congruencia de triángulos, hay que practicar lo aprendido a través de la siguiente actividad.

Se trata de identificar en los ejemplos que se mostrarán, cuáles son los triángulos que cumplen con las características para establecer una congruencia y cuál sería el criterio que se puede aplicar a esta pareja de triángulos.

Debes observar con detenimiento los ejemplos, en cada situación e identificar el criterio que les corresponde.

Situación 1.

Juan realizó el boceto de un molde en papel y posteriormente, construyó el molde basado en el boceto. Observa con detenimiento los triángulos 1, 2 y 3.

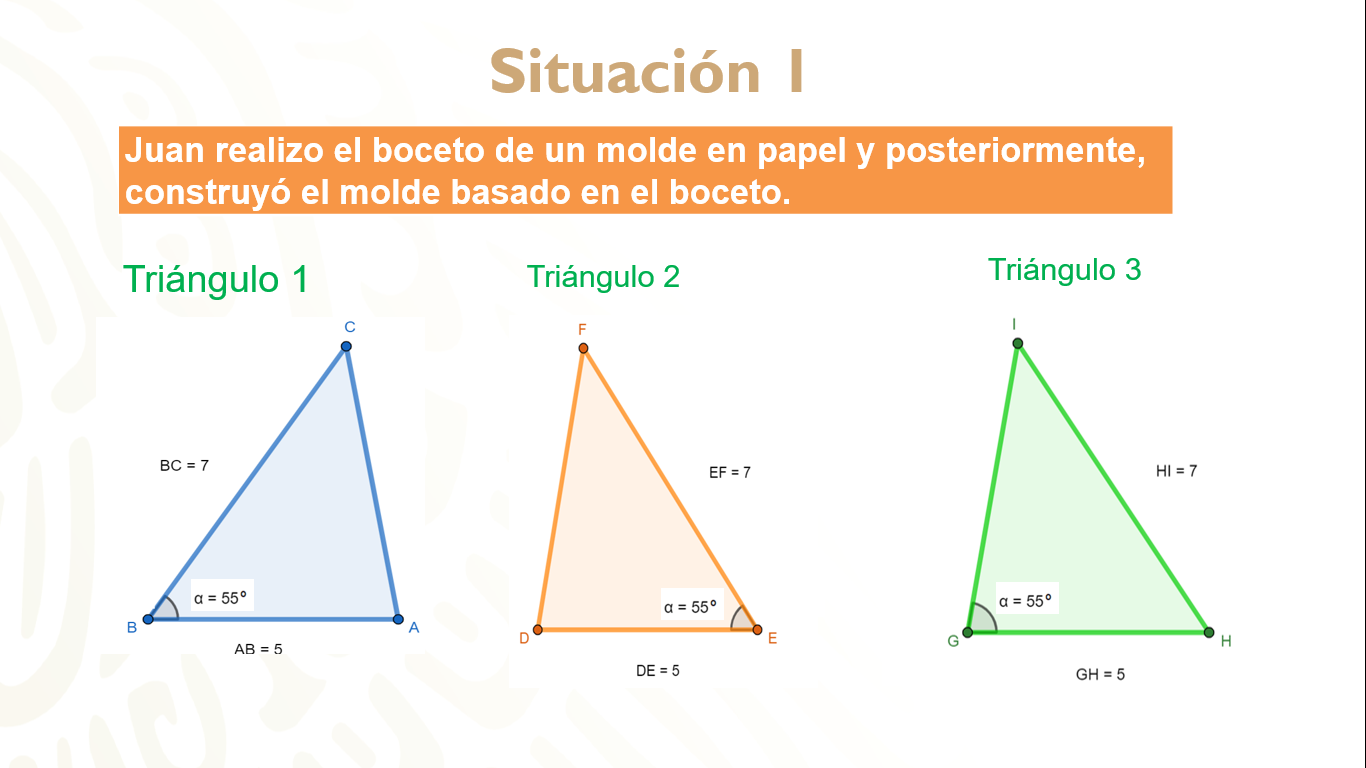
Puedes identificar:

• ¿Cuál de los siguientes triángulos corresponden al boceto y al molde?
• ¿Qué criterio de congruencia te permite comprobar tu respuesta?
• ¿Lograste encontrar los triángulos congruentes?

Verifica tus respuestas.

Analiza la información que te proporcionan las imágenes. En todos los triángulos te dan la medida de dos de sus lados y un ángulo, por lo que el criterio a utilizar es lado, ángulo, lado o LAL.

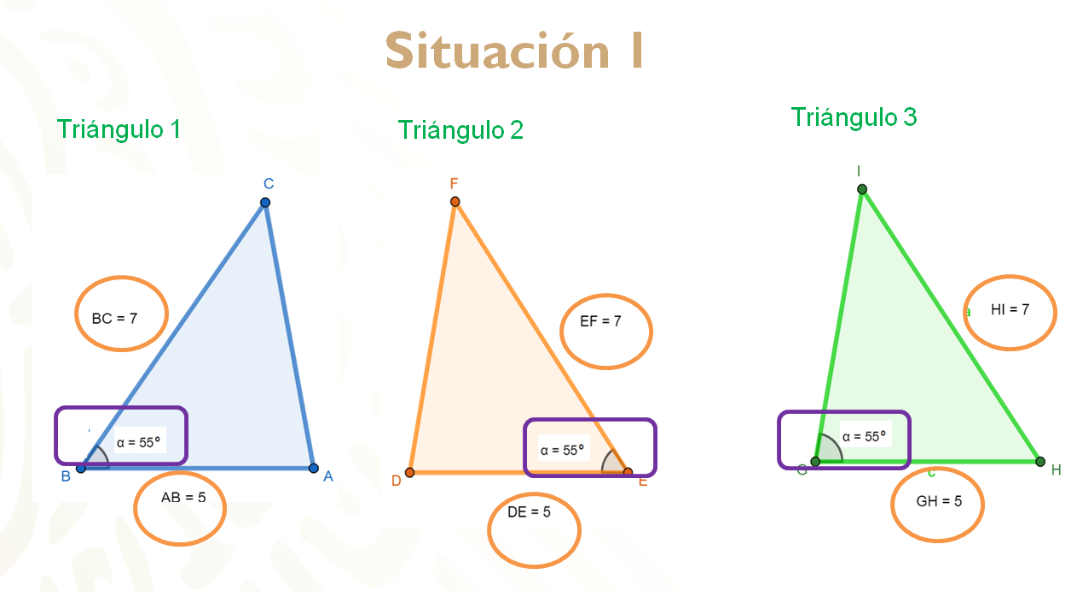
De igual manera, puedes observar que los tres triángulos tienen las mismas medidas, entonces se te pregunta:

• ¿Los tres son congruentes?
• ¿Por qué sí o por qué no?
• ¿Cuál de ellos no es congruente con los otros dos?

Si observaste detenidamente, el triángulo 3 tiene todos los datos iguales a los anteriores, pero el ángulo que es igual no está comprendido entre los dos lados que son congruentes, situación que sí sucede en los triángulos 1 y 2. Por lo tanto, los triángulos congruentes serían el número 1 y el número 2, que cumplen con el criterio LAL.

Ahora solo falta establecer la correspondencia con cada dato.

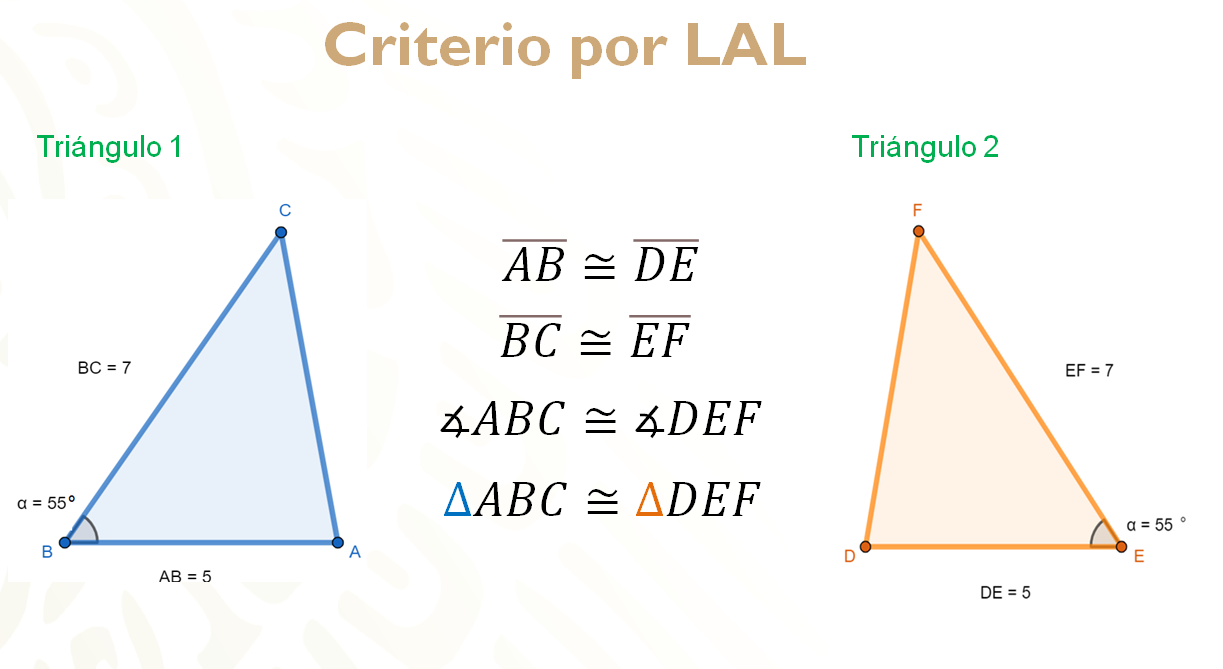
El lado AB es congruente al lado DE y el lado BC es congruente al lado EF. El ángulo ABC es congruente al ángulo DEF, por lo tanto, los triángulos ABC y DEF son congruentes entre sí.

Al hacer referencia que ambos son congruentes, uno de ellos fue el molde y el otro el boceto.

Situación 2.

Hay que revisar un segundo ejemplo.

En una fábrica se utilizan varias máquinas que cortan un único triángulo que se utiliza para los señalamientos en la vía pública, pero una de las máquinas tuvo una falla y produjo triángulos diferentes a los esperados.

Revisa las siguientes imágenes.

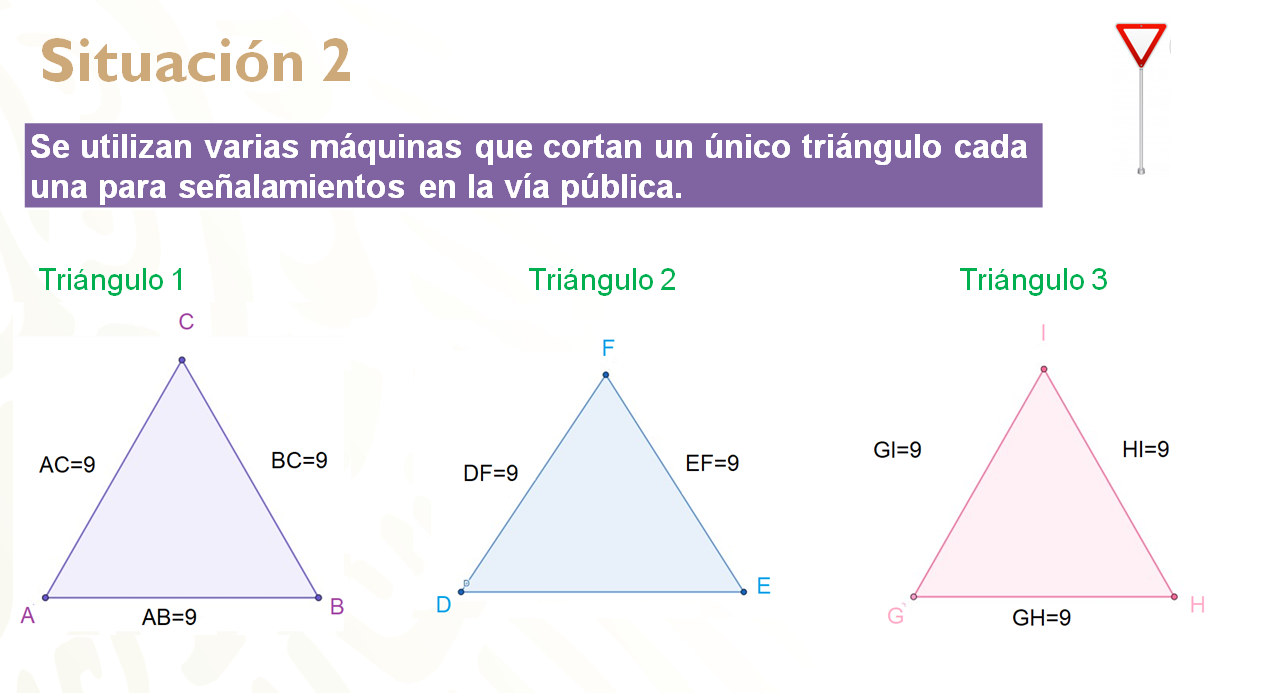
De acuerdo con la información que proporciona cada triángulo.

• ¿Cuál de los triángulos es el defectuoso?
• ¿Qué criterio te ayudaría a establecer que los otros triángulos son congruentes?
• ¿Lograste identificar los triángulos qué son congruentes?

Compara tus respuestas, con la solución que a continuación se te comparte.

En este ejemplo los triángulos solo poseen la medida de los lados. Por lo tanto, el criterio que te permite establecer la congruencia de los triángulos es lado, lado, lado o LLL.

Podrás observar que los tres lados del triángulo 1 y el triángulo 3 tienen las mismas medidas, lo que significa que tienes dos triángulos equiláteros congruentes. Sin embargo, la información del triángulo 2 sólo permite conocer dos de sus lados, lo cual deja incompleta la información y no se podría establecer una congruencia.

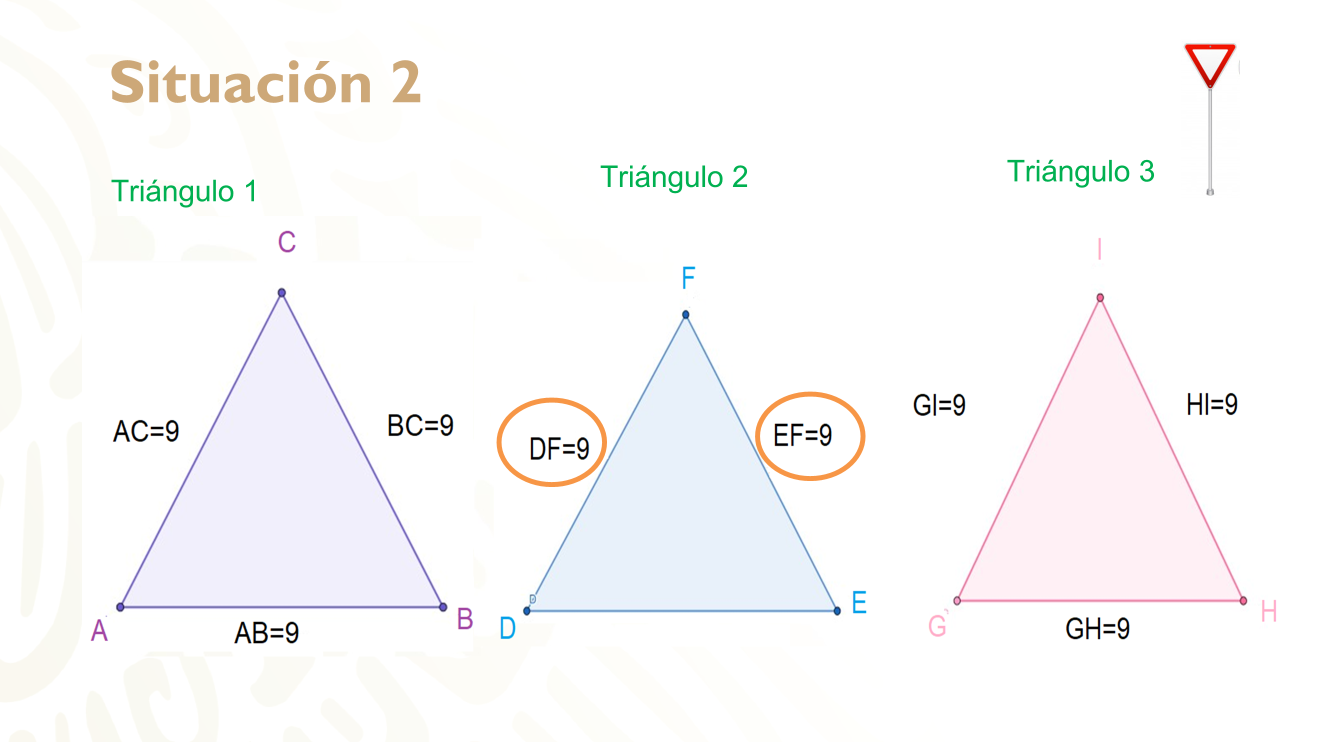
Ahora hay que establecer una congruencia entre el triángulo 1 y el triángulo 3 utilizando la información de cada uno.

Estableciendo la correspondencia entre el lado AB, que es congruente con el lado GH: el lado BC es congruente al lado HI y el lado AC es congruente al lado GI. De esta manera, se puede establecer que el triángulo ABC es congruente al triángulo GHI.

Verificado lo anterior, se puede decir que el triángulo 1 y el triángulo 3 fueron elaborados correctamente.

Situación 3.

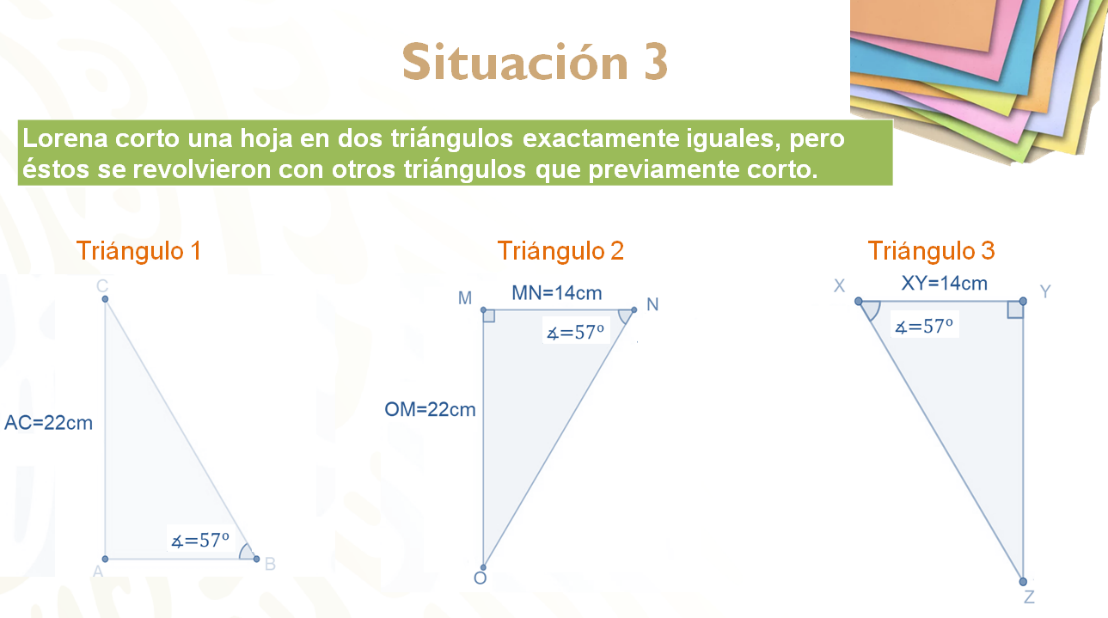
Lorena cortó una hoja en dos triángulos exactamente iguales y se los entregó a su hermana, pero ella los revolvió con otros triángulos que previamente cortó y ahora no logra identificar cuáles son los triángulos que le entregó Lorena. Revisa la información con la que cuentan.

De los siguientes ejemplos.

• ¿Cuáles serían los triángulos que entregó Lorena a su hermana?
• ¿Qué criterio de congruencia justifica esa respuesta?

¿Ya tienes las respuestas?

Revisa las soluciones, para que las compares con tus respuestas.

Probablemente en este ejemplo fue más complicado encontrar la congruencia entre los triángulos debido a que aparentemente ningún triángulo proporciona la misma información. Hay que comenzar analizando cada uno de ellos.

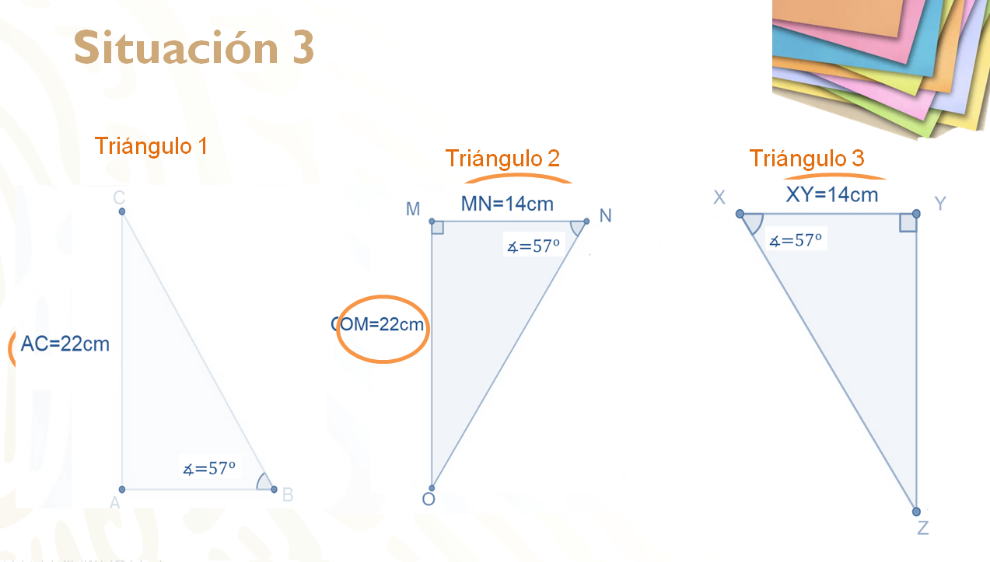
El primer triangulo te proporciona la medida de un lado y un ángulo. Lo cual no es suficiente para establecer un criterio de congruencia.

El segundo triángulo proporciona la información de un ángulo y dos lados, pero está marcado un ángulo recto, el cual por definición mide 90º, por lo que el triángulo dos realmente te está proporcionando cuatro datos.

El triángulo 3 te da la medida de un lado y un ángulo, pero al igual que la figura anterior, muestra un ángulo recto. Por lo tanto, del triángulo tienes el conocimiento de tres datos, que son la medida de un lado y dos ángulos.

Con este análisis más detallado de los triángulos ¿puedes identificar los triángulos congruentes y bajo qué criterio?

Si se pueden identificar. Los triángulos congruentes son el triángulo 2 y el triángulo 3, por el criterio que es: ángulo, lado, ángulo o ALA.

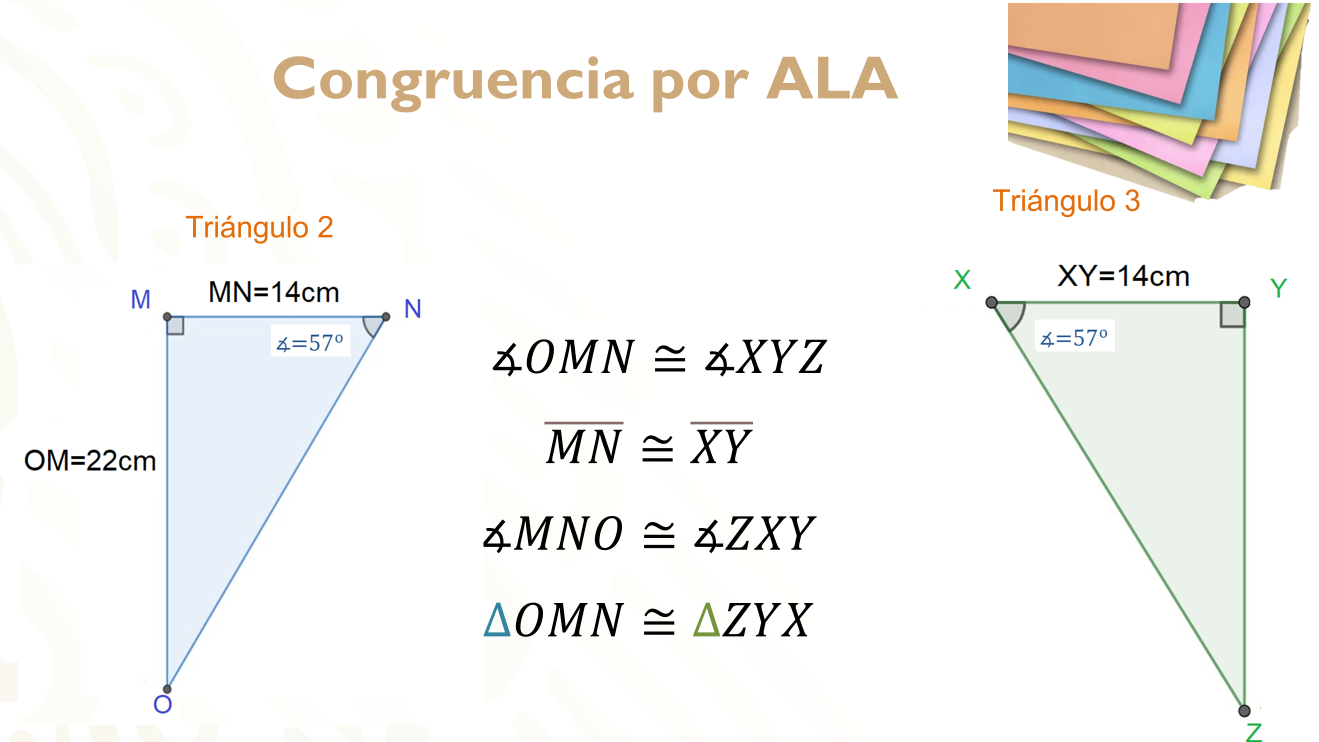
Se comienza estableciendo la congruencia entre el ángulo OMN y el ángulo XYZ al ser rectos. La medida de los lados MN y XY es la misma, por lo tanto, ambos son congruentes. El ángulo MNO es congruente al ángulo ZXY, debido a que ambos miden 57º.

Cumpliendo cada uno de estos criterios, se puede concluir que el triángulo OMN es congruente al triángulo ZYX.

Con las actividades anteriores se logró identificar la información mínima necesaria que deben tener los triángulos para establecer una congruencia entre ellos.

¿Qué te parece si ahora que conoces los criterios de congruencia e identificas cada uno de ellos, los utilizas para resolver otros problemas que se presentan en la vida diaria?

Como, por ejemplo, un topógrafo que necesita medir distancias que bajo ciertas circunstancias son inalcanzables.

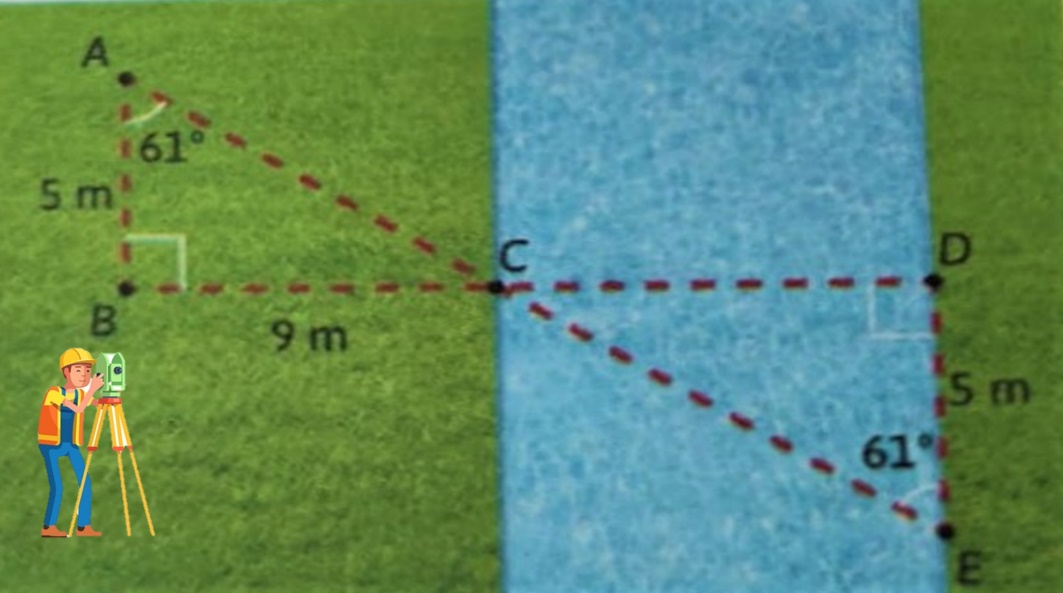
Se necesita medir el ancho de un arroyo, para ello, un topógrafo colocó postes en los puntos A, B, C, D y E. En la imagen se muestran algunas de las medidas que tomó y obtuvo las medidas que se muestran.

Responde aplicando los criterios de congruencia de triángulos, lo siguiente:

¿Cuánto mide el ancho del arroyo y qué criterio de congruencia permite establecer la medida?

Este problema es muy interesante, para resolverlo, observa la imagen y anota los datos ya conocidos.

Lo que se puede observar a simple vista es que el topógrafo al colocar los postes formó dos triángulos, el primero lo puedes nombrar geométricamente a partir de sus tres vértices. Por ello, se dice que tienes un triángulo ABC y un segundo triángulo CDE.

Organiza la información que la imagen te proporciona.

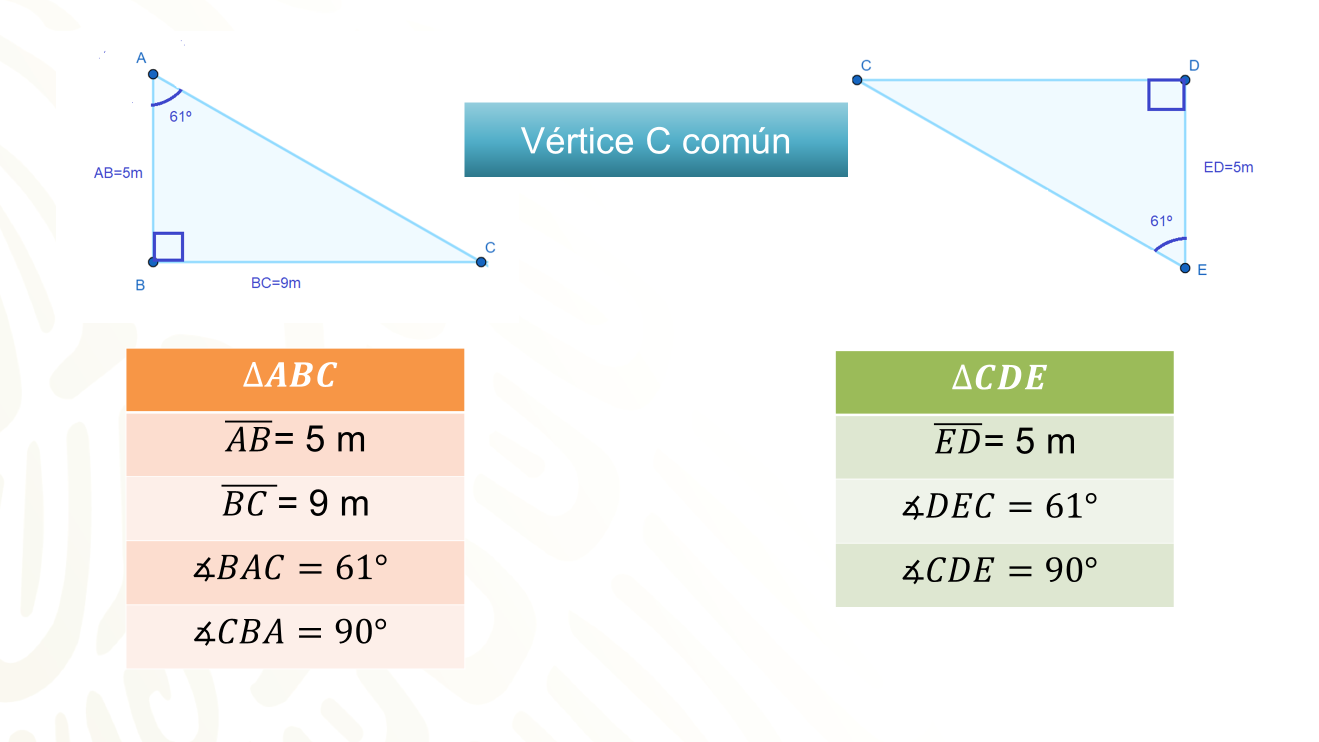
Del triángulo ABC, el segmento AB mide 5 m y el segmento BC mide 9 m. Los ángulos que los conforman, de los cuales conoces la medida, son: El ángulo BAC, que mide 61° y el ángulo CBA, que es un ángulo recto, por lo que mide 90º.

En el segundo triángulo tienes el segmento ED, que mide 5 m el ángulo DEC de 61° y el ángulo CDE, que también es un ángulo recto.

Y ambos triángulos tienen al vértice C en común.

Ya tienes todos los datos ordenados e identificados.

¿Ya encontraste la relación entre ambos triángulos?

Observa nuevamente los datos de las tablas y revisa que datos tienes en común.

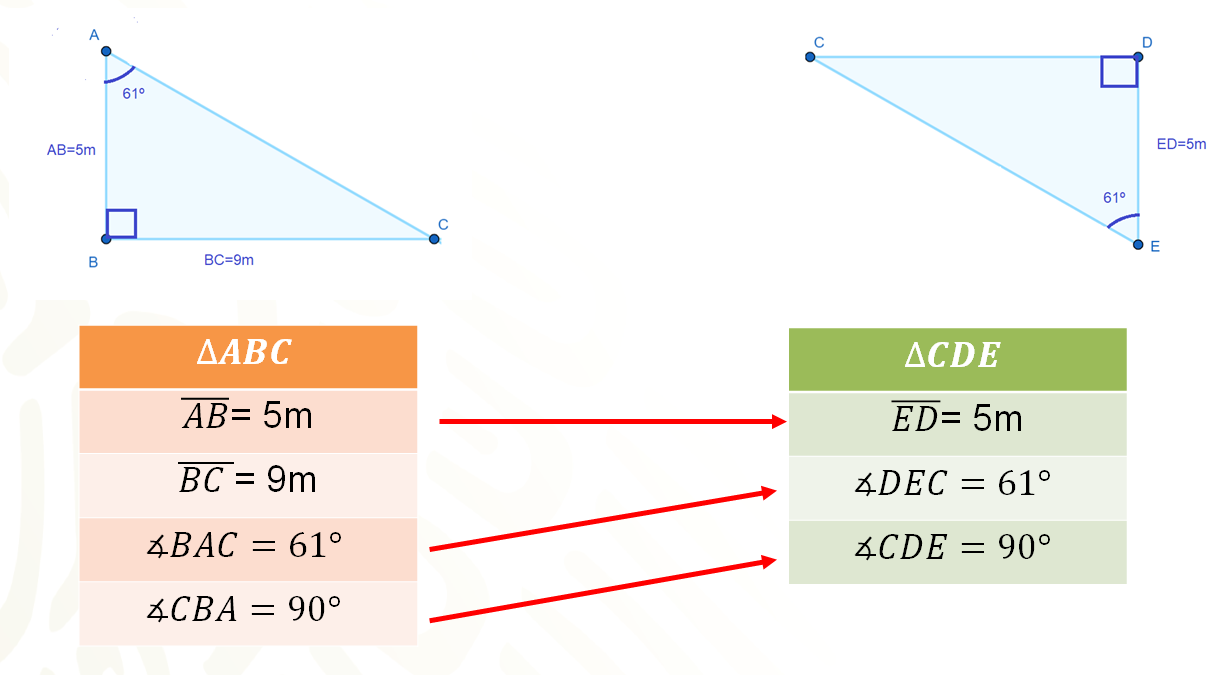
Puedes usar el segmento AB del triángulo ABC y el segmento ED del triángulo CDE, ya que son lados correspondientes y miden lo mismo.

Lo mismo ocurre con el ángulo BAC y el ángulo DEC que miden 61º. Además, el ángulo CBA y el ángulo CDE son ángulos rectos, es decir miden 90°.

Con esta información sabes, ¿qué criterio debes utilizar?

Es momento de demostrar la congruencia utilizando el criterio ALA.

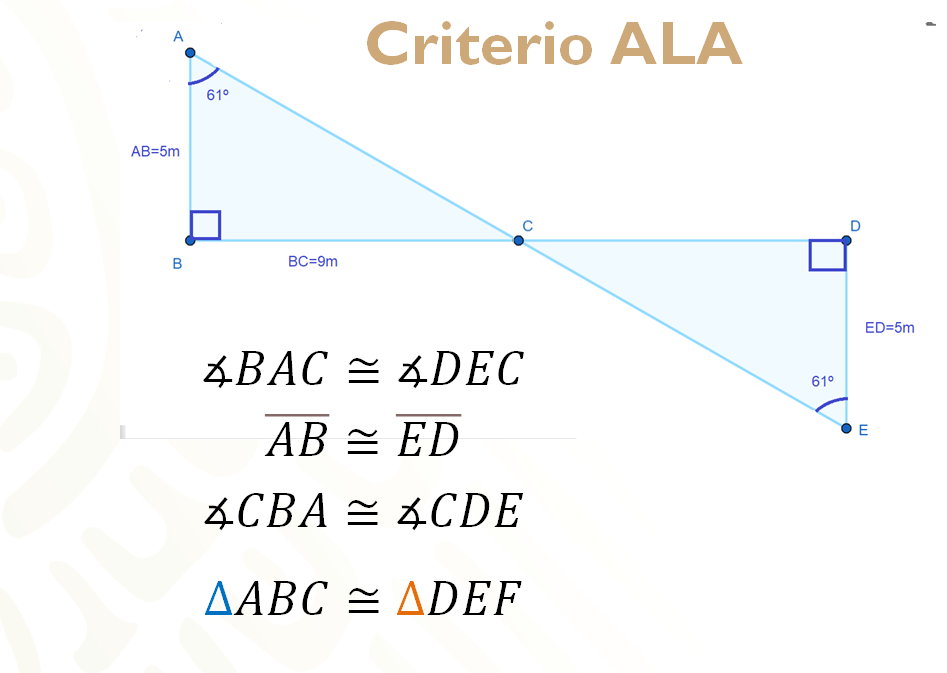
El ángulo BAC es congruente al ángulo DEC.

El lado AB es congruente al lado ED.

El ángulo CBA es congruente al ángulo CDE.

De esta manera se ha demostrado que el triángulo ABC es congruente al triángulo CDE.

Ahora que ya sabes que los dos triángulos formados por el topógrafo son congruentes.

• ¿Cómo usas esta información para encontrar el ancho del río?
• ¿Qué opinas?
• ¿Ya tienes la respuesta?

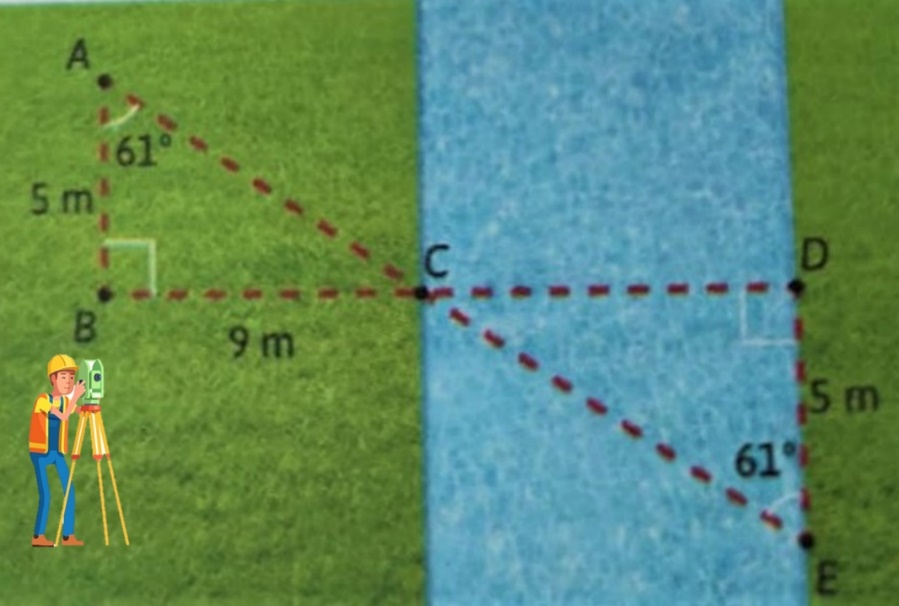
El ancho del arroyo mide lo mismo que el segmento BC, ya que es el lado homólogo al segmento CD, quiere decir que el ancho del arroyo mide 9 metros.

Se espera que estos aprendizajes te sean productivos. No olvides compartir tus dudas con tu maestra o maestro de asignatura a la distancia.

El reto de hoy:

Practica lo aprendido en esta sesión a través de tu libro de texto en el aprendizaje esperado o busca otras actividades que se relacionen con este aprendizaje. Pon a prueba tus conocimientos, desafíate y siempre busca más.

Asimismo, concluye los ejercicios que se te solicitaron en el desarrollo de la sesión, en caso de que no los hayas terminado.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/

1